Виды треугольника периметр треугольника (2 видео)

Треугольник — определение и основные свойства и виды треугольника

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Содержание

Определение треугольника
Высота треугольника
Виды треугольника
Виды треугольников по углам
Виды треугольников по сторонам
Свойства сторон треугольника
Правило существования треугольника
Свойство углов в треугольнике
Элементы композиции
Виды треугольников по длине сторон. Периметр треугольника.
Формулы определения периметра, площади и сторон треугольника
Классификация треугольников
Описание
Примеры
Видео
Видео

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Видео:Математика 5 класс (Урок№28 - Треугольники.)Скачать

Виды треугольника

Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Видео:Математика 6 класс. Треугольник. Виды треугольников. ЕГЭ, ОГЭ, ЦТ, экзаменСкачать

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

Ответ: .

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

Видео:Треугольники. 7 класс.Скачать

Виды треугольников по длине сторон. Периметр треугольника.

Билет №1

Виды треугольников по длине сторон. Периметр треугольника.

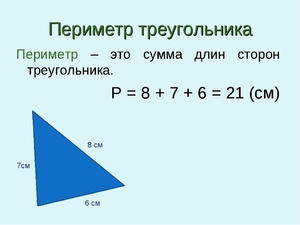
Равнобедренный (равны две стороны), разносторонний (все стороны по величине разные), равносторонний -все стороны равны Периметром треуг называется сумма длин его сторон)

Смежные углы (определение). Теорема о сумме смежных углов.

Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными лучами (т.е. имеют общее начало и дополняют друг друга до прямой).

Сумма смежных углов равна 180°.

Дано: ∠АОВ и ∠ВОС смежные.

Доказать: ∠АОВ + ∠ВОС = 180°

∠АОС = ∠АОВ + ∠ВОС по свойству измерения углов,

∠АОС = 180°, так как является развернутым, ⇒ ∠АОВ + ∠ВОС = 180°

3. Задача по теме «Признаки равенства треугольников».

Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD.

Билет №2

Отрезок (определение). Середина отрезка. Основное свойство расположение точек на прямой.

Отрезок — это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину.
Середина отрезка — это точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка.

из трёх точек на прямой одна и только одна лежит между двумя другими.

Свойства равнобедренного треугольника (доказательство одного из них).

Свойства равнобедренного треугольника:

1. В равнобедренном треугольнике углы при основании равны.

пусть АВС — равнобедренный треуг с основанием АВ. Докажем, что у него А= В.

Тр САВ равен тр СВА по первому признаку равенства треугДействительно, СА=СВ, СВ=СА, угол С= углу С.Из равенства треугольников следует, что угол А= углу В. Теорема доказана.

2 В равнобедренном треуг биссектриса , проведённая к основанию , является медианной и высотой .

Рассмотрим треугольники ACF и BCF (важно правильно их назвать!)

1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))

2) ∠ACF=∠BCF (так как CF — биссектриса по условию).

3) сторона CF — общая.

Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон и углов.

Таким образом, AF=BF, следовательно, CF — медиана.

∠AFC=∠BFC. А так как эти углы — смежные, значит, они прямые: ∠AFC=∠BFC=90º.

Значит, CF — высота.

Что и требовалось доказать.

3. Задача по теме «Окружность и ее элементы».

Найдите длину радиуса окружности, если длина диаметра равна 14,5 см.

Билет № 3

Основные геометрические фигуры на плоскости. Основное свойство принадлежности точек и прямых.

Основными геометрическими фигурами на плоскости являются точка и прямая. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

Построение треугольника по трём сторонам.

Даны три отрезка: a,b иc, равные сторонам искомого треугольника..

В этом случае перед началом построения необходимо убедиться, исполняется ли неравенство треугольника (длина каждого отрезка меньше суммы длин двух остальных отрезков), и эти отрезки могут быть сторонами треугольника.

1. Провести прямую.

2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B.

3. Провести окружность с центром A и радиусом, равным отрезку b.

4. Провести окружность с центром B и радиусом, равным отрезку c.

5. Точка пересечения окружностей является третьей вершиной искомого треугольника.

3. Задача по теме «Вертикальные углы».

Один из вертикальных углов равен 45º. Найдите остальные углы.

Билет № 4

1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

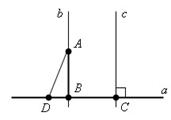
Высота треугольника — это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение.

2. Теорема о свойстве катета, лежащего против угла в 30º.

Так как сумма острых углов прямоугольного треугольника равна 90º, то∠B=90º-∠A=90º-30º=60º.Построим треугольник ADC, равный треугольнику ABC.В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).Отсюда, ∠BAD=∠CAD+∠CAB=60º.Следовательно, в треугольнике ABD все углы равны:∠BAD=∠D=∠B=60º.Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.BC=DC (по построению), поэтому 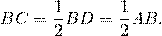Что и требовалось доказать.

3. Задача по теме » Признаки параллельности прямых».

Один из внутренних накрест лежащих углов, образованных при пересечении двух параллельных прямых третьей прямой, равен 50º. Найдите градусные меры остальных углов.

Билет № 5

Билет №6

Билет № 7

Билет № 8

Билет № 9

1. Углы, образованные при пересечении двух прямых секущей. Аксиома параллельности прямых (без доказательства)

При пересечении прямых секущей образуются такие пары углов:

· Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами.

· Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами.

· Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.

Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной

Билет № 10

1. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников (без доказательства).

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)

Признак равенства прямоугольных треугольников по двум катетам

Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и гипотенузе

Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

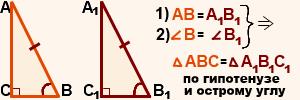
Признак равенства по гипотенузе и острому углу

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Признак равенства прямоугольных треугольников по катету и острому углу

Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Билет № 11

Билет № 12

1. Высота, биссектриса, медиана треугольника (определения).

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса — это отрезок, делящий угол треугольника на две равные части.

Билет № 13

Билет № 14

Деление отрезка пополам.

	Пусть AB данный отрезок. Описываем окружность радиусом AB с центром в точках A и B. Пусть эти окружности пересекаются в точках С1 и С2.
	Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB.
	Док-во. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 — общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB.

3. Задача по теме » Смежные углы».

Найдите смежные углы, если один из них в два раза больше другого.

Билет № 15

Неравенство треугольника.

Теорема.
Каждая сторона треугольника меньше суммы двух других сторон.

Рассмотрим произвольный треугольник ABC и докажем, что AB

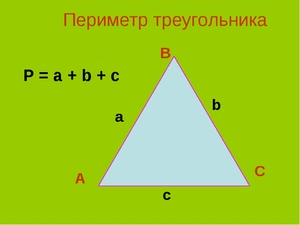
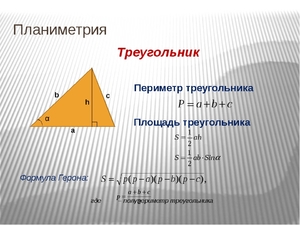
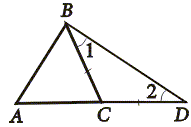В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB

Билет № 16

Билет № 17

Билет № 18

1. Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника (без доказательства)

Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.

1. Сумма острых углов равна 90
2. Катет лежащий против угла 30 равен половине гипотенузы
3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий против него равен 30

Билет № 19

Билет № 20

Теорема.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Доказательство

Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.

3. Задача по теме «Сумма углов треугольника «.

Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.

Билет №1

Виды треугольников по длине сторон. Периметр треугольника.

Последнее изменение этой страницы: 2019-04-21; Просмотров: 861; Нарушение авторского права страницы

Видео:Виды треугольниковСкачать

Формулы определения периметра, площади и сторон треугольника

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

Из этого видео вы узнаете, как найти площадь треугольника.

Видео:Треугольник и его виды. 5 классСкачать

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

Равноугольный: все вершины равны 60°, будет и равносторонним.
Равнобедренный: при равенстве двух граней углы на основании равны.
Разноугольный: все вершины разные, ребра у него тоже разные.
Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.

Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Описание

Чтобы описать любой треугольник, достаточно указать:

Одну сторону и прилегающие к ней углы.
Две стороны и угол между ними.
Три стороны.

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Видео:Геометрия 7 класс. Треугольник. Определение, неравенство треугольника. Виды треугольников.Скачать

Примеры

Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .

Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:

S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .

Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .

Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .

Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео:Виды треугольниковСкачать