Вершины квадрата лежат в треугольник

Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №16
к главе «§11. Подобие фигур».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Видео:Вершины K и L квадрата KLMN с центром O лежат на стороне AB треугольника ABC.Скачать

В треугольник ABC вписан квадрат так, что две его вершины лежат на стороне AB одной вершине — на сторонах AB и BC?

Геометрия | 5 — 9 классы

В треугольник ABC вписан квадрат так, что две его вершины лежат на стороне AB одной вершине — на сторонах AB и BC.

Найдите площадь квадрата, если AD = 40 см, а высота, проведенная из вершины C, имеет длину 24 см.

Обозначим основание высоты треугольника буквой Н, верхнюю сторону вписанного квадрата КМ, пересечение высоты ВН треугольника со стороной КМ квадрата буквой Е

Стороны квадрата параллельны.

Рассмотрим треугольники АВС и КВМ

Они подобны по равным углам : один общий, другие при параллельных основаниях.

Пусть сторона квадрата КМ = а.

Тогда ВЕ = 24 — а

Из подобия треугольников справедливо отношение

40 : а = 24 : (24 — а)

S = а² = 15² = 225 см².

Видео:✓ Квадрат вписан в прямоугольный треугольник | Ботай со мной #129 | Борис ТрушинСкачать

В треугольник, основание которого 9 см?

В треугольник, основание которого 9 см.

Вписан квадрат так , что две его вершины лежат на основании треугольника, а две другие — на боковых сторонах.

Найдите высоту треугольника, если сторона квадрата равна 5 см.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Одна из вершин квадрата со стороной а совпадает с вершиной прямоугольного треугольника, другие лежат на катетах и гипотенузе?

Одна из вершин квадрата со стороной а совпадает с вершиной прямоугольного треугольника, другие лежат на катетах и гипотенузе.

Один из углов равен 30 градусов.

Найдите длину гипотенузы.

Видео:№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

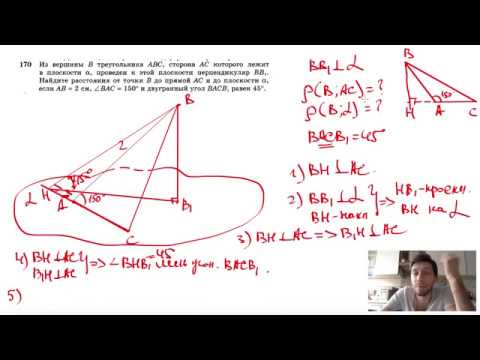
В равнобедренный треугольник, основание которого на 7 м больше высоты, вписан квадрат так, что две его вершины лежат на боковых сторонах треугольника, адве другие — на его основании?

В равнобедренный треугольник, основание которого на 7 м больше высоты, вписан квадрат так, что две его вершины лежат на боковых сторонах треугольника, адве другие — на его основании.

Выразите площадь треугольника S как функцию длины x сторон квадрата.

Найдите площадь треугольника, если известно, что сторона вписанного квадрата равна 12 см.

Видео:№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

В треугольнике АВС сторона АВ равна a, а высота СН равна h?

В треугольнике АВС сторона АВ равна a, а высота СН равна h.

Найдите сторону квадрата, вписанного в треугольник АВС так, что две соседние вершины квадрата лежат на стороне АВ, а две другие — соответственно на сторонах АС и ВСю Заранее спасибо!

Видео:Геометрия Вершины квадрата ABCD лежат на окружности. На дуге AB отмечена произвольная точка MСкачать

В равнобедренный треугольник с основанием 10 см и боковой стороной 5 * корень из 2 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины — на боковых сторонах?

В равнобедренный треугольник с основанием 10 см и боковой стороной 5 * корень из 2 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины — на боковых сторонах.

Найдите сторону квадрата.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие на катетах?

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие на катетах.

Найдите гипотенузу треугольника, если сторона квадрата равна a см.

Видео:Уравнения стороны треугольника и медианыСкачать

Основание треугольника 5 см высота проведенная к этому основани равна 3 см?

Основание треугольника 5 см высота проведенная к этому основани равна 3 см.

В треуголник вписан квадрат так что его 2 вершины лежат на основании а две другие на боковых сторонах вычислите сторону квадрата.

Видео:#38 КВАДРАТ В ТРЕУГОЛЬНИКЕ // НАЙТИ ПЛОЩАДЬСкачать

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие на катетах?

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие на катетах.

Найдите гипотенузу треугольника, если сторона квадрата равна 2 сантиметра.

Видео:Геометрия В треугольник ABC вписан квадрат так, что две его соседние вершины принадлежат стороне ACСкачать

ПОЖАЛУЙСТА РЕШИТЕ?

В равнобедренный треугольник с основанием 12см и высотой 8см вписан квадрат так, что две его вершины лежат на основании треугольника, а две оставшиеся — на его боковых сторонах.

Найти сторону квадрата.

В ответе получается 6, 12.

Видео:№581. Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы доСкачать

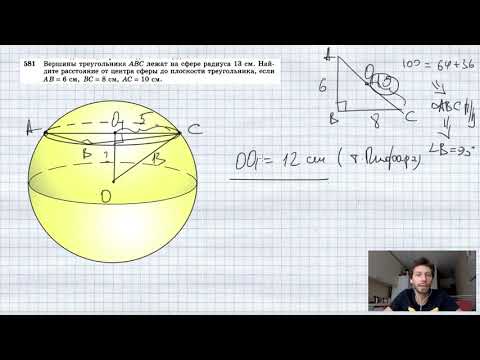
В равнобедренный треугольник с основанием 12см и высотой 8см вписан квадрат так, что две его вершины лежат на основании треугольника, а две оставшиеся — на его боковых сторонах?

В равнобедренный треугольник с основанием 12см и высотой 8см вписан квадрат так, что две его вершины лежат на основании треугольника, а две оставшиеся — на его боковых сторонах.

Найти сторону квадрата.

В ответе получается 6, 12.

Перед вами страница с вопросом В треугольник ABC вписан квадрат так, что две его вершины лежат на стороне AB одной вершине — на сторонах AB и BC?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Очевидно, что треугольник АВС — прямоугольный)) и по условию равнобедренный, т. Е. углы А и В равны и = 45° треугольник EFВ тоже прямоугольный, с острым углом В = 45°, следовательно, он тоже равнобедренный : EF = CF(квадрат) = BF ВС = 12 = BF + СF =..

В прямоугольном треугольнике АВС медианы СМ, ВN и АК. Медиана из прямого угла равна половине гипотенузы СМ = с / 2 (свойство). АС = с * Cosα. BC = c * Sinα. По Пифагору : АК = √(АС² + ВС² / 4) = √(4с² * Cos²α + c²Sin²α) / 2 = (c / 2) * √(4 * Cos²..

AB = AM, т. К. треуг. ABM равнобедренный, потому что углы при основании равны, значит боковые стороны (AB и AM) равны, и равны они 4, 5 см. AD равен AM + MD = 4, 5 + 2, 5 = 7 см. Pabcd равен 7 + 7 + 2, 5 + 2, 5 = 19 см. 2 способ нахождения Pabcd..

Видео:Геометрия В треугольнике ABC известно, что угол C = 90, AC = BC = 14 см. Две стороны квадрата CDEFСкачать

Треугольник вписанный в окружность

Видео:Чему равна площадь квадрата , размещённого в треугольнике.Скачать

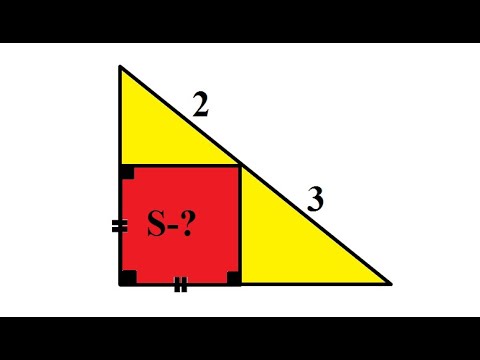
Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:№9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости αСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:№562. В треугольнике ABC сторона АВ равна а, а высота CH равна h. Найдите сторону квадратаСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

🎬 Видео

Найти площадь большого треугольникаСкачать

№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

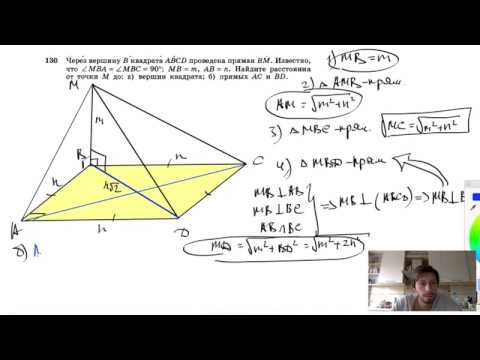
Геометрия Дан квадрат, две вершины которого лежат на окружности радиуса R, две другие - наСкачать

№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать