Треугольник серпинского python рекурсия (5 видео)

Треугольник Серпинского¶

Ещё один фрактал, обладающий свойством самоподобия, — это треугольник Серпинского. Его пример показан на рисунке 3. Треугольник Серпинского иллюстрирует трёхходовой рекурсивный алгоритм. Процедура его отрисовки вручную очень проста. Начинаем с большого треугольника, который делим на четыре маленьких, связанных с серединами сторон первоначального. Игнорируя вновь созданный внутренний треугольник, делаем всё то же самое для каждого из трёх угловых. Каждый раз при создании нового набора треугольников, вы рекурсивно применяете эту процедуру к трём меньшим угловым фигурам. Так можно продолжать до бесконечности (если у вас достаточно острый карандаш). Перед тем, как продолжить чтение, можете попробовать самостоятельно нарисовать треугольник Серпинского, используя описанный метод.

Рисунок 3: Треугольник Серпинского.

Поскольку мы можем повторять этот алгоритм до бесконечности, что сделать базовым случаем? Им станет произвольное число — сколько раз мы хотим разделить треугольник на части. Иногда это число называют “степенью” фрактала. Каждый раз при рекурсивном вызове мы вычитаем из степени единицу, пока она не станет равной нулю. Тогда мы останавливаем рекурсию. Код, генерирующий треугольник Серпинского с рисунка 3, показан в ActiveCode 4.

Рисование треугольника Серпинского (lst_st)

Программа из ActiveCode 4 следует изложенным выше идеям. Первое, что делает sierpinski , — это прорисовывает внешний треугольник. Затем идут три рекурсивных вызова, по одному для каждого из новых угловых треугольников, полученных после соединения средних точек сторон. Мы снова используем стандартный модуль Python turtle . Вы можете изучить в подробностях все его методы, воспользовавшись командой help(‘turtle’) в командной строке Python.

Посмотрите на код и подумайте, в каком порядке будут прорисовываться треугольники. Поскольку точный порядок углов определяется спецификацией начального набора, давайте предположим, что углы идут в следующем порядке: нижний левый, верхний, нижний правый. Так как функция sierpinski вызывает сама себя, вычисление будет идти к наименьшему возможному треугольнику в левом нижнем углу, а затем уже будут заполняться остальные треугольники в обратном порядке. Потом заполнятся треугольники в верхнем углу — к наименьшему и самому верхнему. Наконец, будут заполнен правый нижний угол, опять же по направлению к наименьшему нижнему правому.

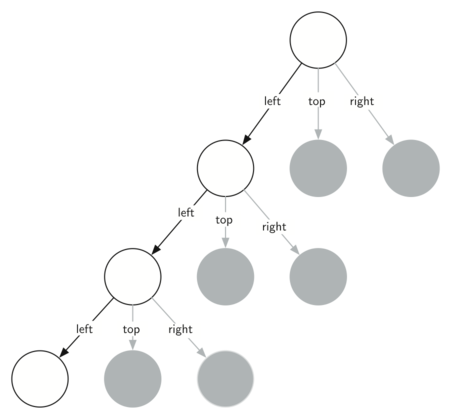
Иногда полезно думать о рекурсивных алгоритмах в терминах диаграммы вызовов функции. Рисунок 4 показывает, что рекурсивные вызовы всегда начинаются слева. Активная функция выделена чёрным, неактивные вызовы — серым. Чем ниже вы спускаетесь по рисунку 4, тем меньше треугольники. Функция заканчивает рисунок одного уровня за один раз; закончив с нижней левой частью, она перемещается к нижней середине и так далее.

Рисунок 4: Построение треугольника Серпинского.

Функция sierpinski сильно зависит от функции getMid . Последняя принимает в качестве аргументов две конечные точки и возвращает точку, находящуюся по середине между ними. В дополнение, ActiveCode 4 содержит функцию раскраски треугольников, использующую методы begin_fill и end_fill из модуля turtle . Это означает, что каждая степень треугольника Серпинского рисуется другим цветом.

readers online now | | Back to top

Видео:Треугольник Серпинского. Пример применения рекурсивной функции.Скачать

Python, Треугольник Серпинского, и не только…

Приветствую читателей. Это моя первая статья на Хабре. В ней я бы хотел поделиться своими экспериментами с алгоритмом построения фракталов путём размещения точек в определённых координатах.

Я не исключаю, что вы можете уже разбираться в теме фракталов, и даже работали с алгоритмом, о котором я буду рассказывать, и что информации об этом много, хоть я и не нашёл какие-то эксперименты с ним. Так что не бейте.

Начнём с рассказа о Треугольнике Серпинского. Это фрактал, то есть, как гласит ошибочная формулировка — само-подобная фигура, (чьи части подобны самой фигуре). Вы наверняка видели Треугольник Серпинского.

Треугольник Серпинского

Существует способ его создания, который мы и будем повторять на языке программирования Python. Сам алгоритм выглядит так:

Бирюзовый квадрат — это строитель.

Эта картинка из программы, которую я написал на Python за пару минут. Использовал библиотеку pyxel, потому что она мне нравится, выглядит приятно, но как потом окажется — имеет недостаточное разрешение, что в нашем случае — сделает трудноразличимым маленькие элементы фрактала.

И тут у меня возникла идея использовать четыре угла вместо трёх. Я ожидал, что получится такой же фрактал, только с четырёхугольниками (Ковёр Серпинского). Результат меня немного не порадовал — всё поле просто заполнялось точками хаотично, и не было никакого результата.

Строитель стремится к центру, немного колеблясь

И я ещё долгое время думал, что такой алгоритм будет работать только с треугольником. Но я ошибался, и совсем недавно решил, что надо делить путь до угла не на два, а на 3 или больше. Однако, это лишь смещало строителя в центр экрана. Но получился неплохой алгоритм проверки случайным чисел (Если точка переместилась в центр, и не выходит из него, значит — алгоритм случайных чисел хороший).

И тут я решил идти в другую сторону, то есть делить путь до угла не на два, а на 1.n, например — на 1.75 Результат стал уже очень заметным. Что-то явно получается.

Что, если использовать 5 углов, а делить ещё на меньшее число, например — 1.5 ?

Можно назвать это «Цветком Левина», в мою честь, если эту фигуру ещё никто не открыл?

Однако, использовать настолько пиксельную библиотеку было плохим вариантом, поэтому я быстро вспомнил pygame, и переписал код уже на неё, так как там можно сделать 240 кадров в секунду, в надежде, что это ускорит процесс, а так же сделать разрешение экрана побольше, что, соответственно — улучшит детализацию.

Тест библиотеки pygame

Алгоритм работает отлично. Значит — можно экспериментировать.

Применяем пять точек и деление на 1.75, чтобы получить наш цветок.

Пятиугольник-цветок тоже работает

Если включить воображение, и преодолеть барьер восприятия в виде кучки пикселей, чему нас учил Майнкрафт — то можно увидеть, что эта фигура так же само-подобна.

Я даже попытался приблизить фрактал путём установки углов за границей экрана.

К сожалению, фракталы почти не имеют практического предназначения, за исключением компьютерной графики, а мой цветок-шестиугольник вряд ли будет выглядеть как-то красиво. Так что я принимаю тот факт, что «исследования» в этом направлении — не оправданы и бесполезны. Просто мне показалось это довольно интересной темой.

Если кто-нибудь из вас владеет быстрым языком типа C++ или C# (Или Assembler?), и может оптимизировать программу настолько, насколько это возможно — то можете попробовать повторить эту программу, но добавив приближение фрактала, например — путём отрисовки установленных точек в координатах, относительных зуму, что можно реализовать через матрицу двумерного масштабирования, а точки записывать списком, чьи элементы состоят из векторов. У меня даже получилось сделать зум и передвижение по фракталу, правда, при масштабировании всё съезжает в правый нижний угол.

Надеюсь, вам было хоть немного интересно. Извиняюсь, если статья оказалась бесполезной/неинтересной, или показалась вам сырой.

Видео:41 Рекурсия в Python. Рекурсивная функция Часть 1Скачать

Треугольник Серпинского

Треугольник Серпинского — это фрактальное и привлекательное фиксированное множество с общей формой равностороннего треугольника . Он рекурсивно делится на более мелкие треугольники.

Примеры :

Подходить :

Sierpinski Triangle will be constructed from an equilateral triangle by repeated removal of triangular subsets.
Steps for Construction :
1 . Take any equilateral triangle .
2 . Divide it into 4 smaller congruent triangle and remove the central triangle .
3 . Repeat step 2 for each of the remaining smaller triangles forever.

Ниже приведена программа для реализации треугольника Серпинского

// C ++ программа для печати треугольника Серпинского.
#include