Треугольник егэ профиль теория

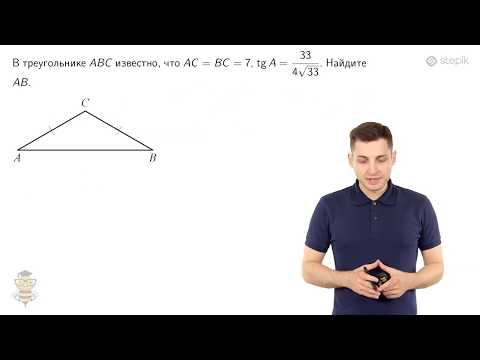
Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

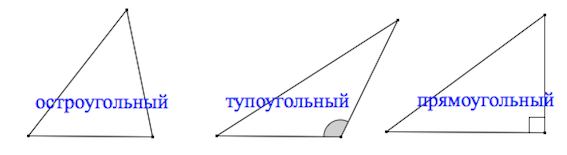
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

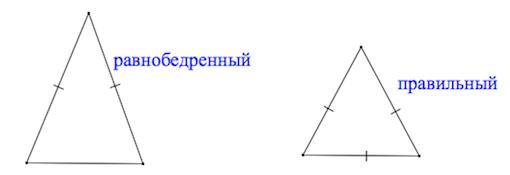
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .

Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

3. Сумма углов треугольника равна 180 º .

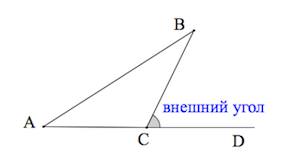
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

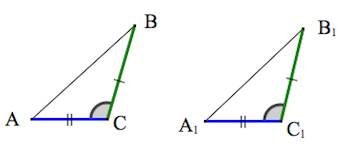
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

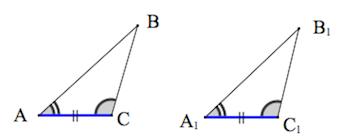
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.

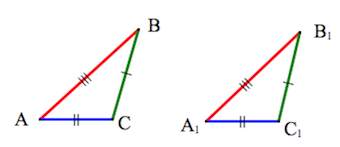
3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

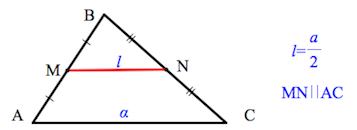
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

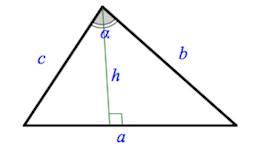
Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо! 😉

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

Видео:Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

Основные факты о треугольниках

Определения

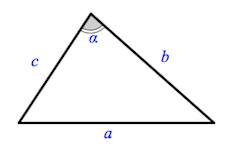
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.

Угол (alpha) называется острым, если (0^circ , прямым – если (alpha=90^circ) , тупым – если (90^circ , и развернутым – если (alpha=180^circ) .

Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.

Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.

Теорема

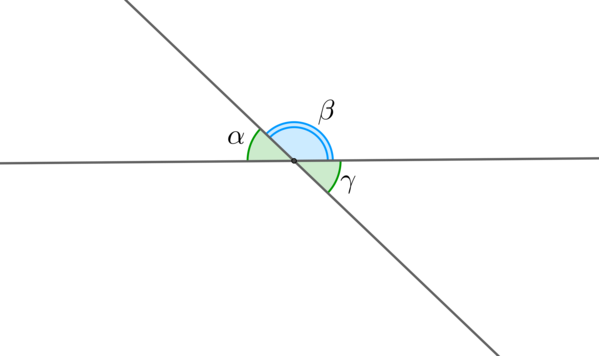
Смежные углы (alpha) и (beta) в сумме дают (180^circ) .

Вертикальные углы равны: (alpha=gamma) .

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Определение

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Две прямые называются перпендикулярными, если угол между ними равен (90^circ) .

Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ) .

Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Замечание

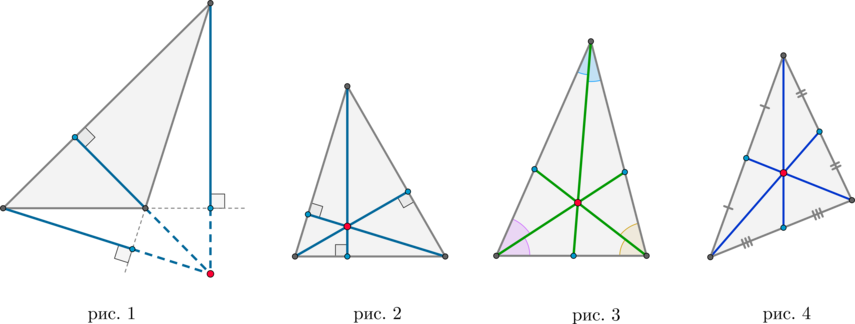
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

Теорема

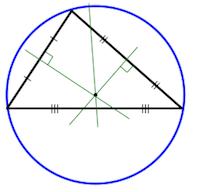
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.

Следствия из аксиомы

1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.

2. Две прямые, параллельные третьей прямой, параллельны.

Теоремы: признаки параллельности прямых

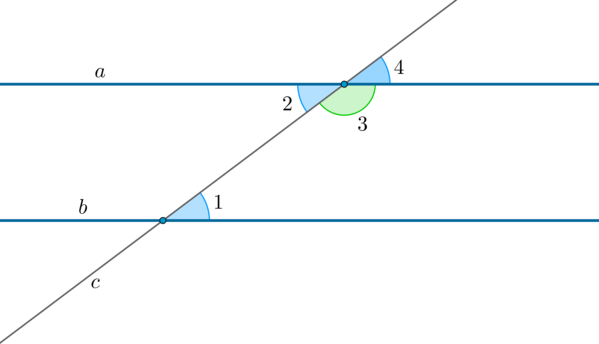
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2) , то такие прямые параллельны.

2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ) , то такие прямые параллельны.

3. Если при пересечении двух прямых (a) и (b) секущей (c) соответственные углы равны: (angle 1=angle 4) , то такие прямые параллельны.

Теоремы: свойства параллельных прямых

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ) .

3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Определения

Треугольник называется остроугольным, если все его углы острые.

Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).

Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).

Теорема

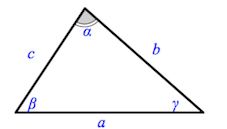
Сумма внутренних углов треугольника равна (180^circ) .

Доказательство

Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A + angle B + angle C = 180^circ) .

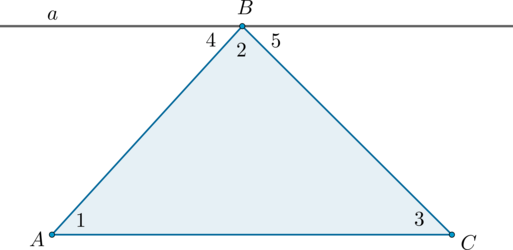
Проведём через вершину (B) прямую (a) , параллельную стороне (AC) .

Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB) , а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC) . Поэтому [begin &angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad (1) end]

Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B) , то есть (angle 4 + angle 2 + angle 5 = 180^circ) . Отсюда, учитывая равенства ((1)) , получаем: (angle 1 + angle 2 + angle 3 = 180^circ) .

Определение

Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.

Теорема

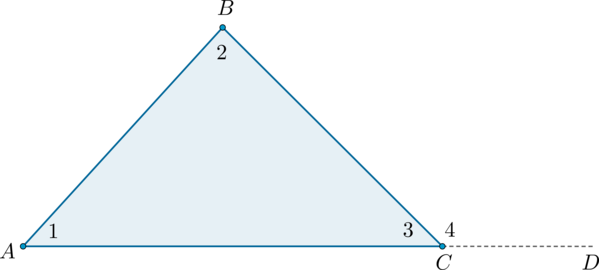
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC) .

Доказательство

Угол (4) – внешний угол треугольника, смежный с углом (3) . Так как (angle 4 + angle 3 = 180^circ) , а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ) , то (angle 4 = angle 1 + angle 2) , что и требовалось доказать.

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

Теорема

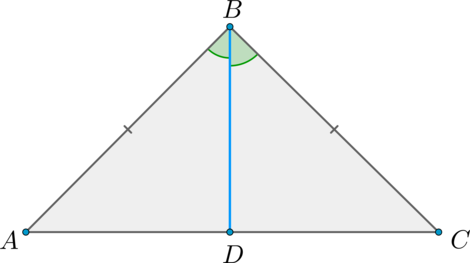
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

Пусть (ABC) – равнобедренный треугольник, (AB = BC) , (BD) – биссектриса (проведённая к основанию).

Рассмотрим треугольники (ABD) и (BCD) : (AB = BC) , (angle ABD = angle CBD) , (BD) – общая. Таким образом, (triangle ABD = triangle BCD) по двум сторонам и углу между ними.

Из равенства этих треугольников следует, что (AD = DC) , следовательно, (BD) – медиана.

Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC) , следовательно, [begin &angle ADB = angle CDB, qquad qquad qquad (2) end] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ) , откуда при учёте ((2)) : (angle ADB = 90^circ = angle CDB) , то есть (BD) – высота.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

В равнобедренном треугольнике углы при основании равны.

Доказательство

Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C) .

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.

В треугольнике против большего угла лежит большая сторона.

Теорема: неравенство треугольника

В треугольнике сумма любых двух сторон больше третьей стороны.

Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.

Определения

В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.

Теоремы: свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна (90^circ) .

2. В прямоугольном треугольнике катет, лежащий против угла (30^circ) , равен половине гипотенузы.

Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла (30^circ) .

Подготовка выпускников к сдаче ЕГЭ, как правило, начинается с повторения базовой теории по планиметрии, в том числе и по теме «Треугольники». Знакомство учащихся с этим разделом геометрии начинается еще в средней школе. Неудивительно, что потребность в повторении основных правил и теории по теме «Треугольник» возникает у многих выпускников. При этом решать планиметрические задачи обязательно должны уметь все учащиеся. Подобные задания включены как в базовый, так и в профильный уровень аттестационного испытания. Разобравшись с теорией и практическими упражнениями, в том числе и на вычисление вертикальных углов треугольника, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение конкурентных баллов по итогам сдачи ЕГЭ.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Готовьтесь к экзамену вместе с образовательным порталом «Школково»

Занимаясь перед сдачей ЕГЭ, многие учащиеся сталкиваются с проблемой поиска базовой теории по геометрии о треугольниках. Школьных учебников в нужный момент может просто не оказаться под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.

Вместе с образовательным порталом «Школково» выпускники смогут качественно подготовиться к сдаче аттестационного испытания. Вся базовая теория о равнобедренных и прямоугольных треугольниках систематизирована и изложена нашими специалистами с учетом богатого опыта в максимально доступной форме. Изучив представленную информацию, школьники смогут вспомнить материал, который вызывает определенные затруднения.

Чтобы хорошо подготовиться к экзамену, учащимся, проживающим в Москве и других городах России, необходимо не только повторить теорию о прямоугольных и равнобедренных треугольниках, но и попрактиковаться в выполнении соответствующих упражнений. Задачи по данной теме вы можете найти в разделе «Каталог». Для каждого задания наши специалисты прописали подробный ход решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут научиться применять на практике теоремы равенства треугольников и другую теорию, которую необходимо усвоить при подготовке к ЕГЭ. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.

Попрактиковаться в решении задач, в которых применяется теория смежных углов и другие теоремы, школьники могут в режиме онлайн.

По желанию учащегося любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию о прямоугольных и равнобедренных треугольниках, выпускник может в дальнейшем вернуться к заданию, которое вызвало затруднения, и обсудить алгоритм его решения с преподавателем.

Видео:ЕГЭ 2023 по математике. Планиметрия: вся теория для №1 из ЕГЭ по профильной математикеСкачать

Справочный материал по теме «Треугольники»

В помощь при подготовке к ЕГЭ и ОГЭ.

Треугольник – это геометрическая фигура, состоящая из трёх точек, которые не лежат на одной прямой и последовательно соединены отрезками.

Видео:Все типы 1 задание ЕГЭ по математике профиль 2024Скачать

Задания нового формата ЕГЭ по английскому языку

Фрагмент выступления М.В. Вербицкой на Всероссийской научно-практической конференции «Требование нового ФГОС 2021. Иностранные языки».

Видео:Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

Практико-ориентированные задачи. Кухня, №1-5

На занятии рассмотрены задачи №1-5 про кухню из ОГЭ по математике (блок практико-ориентированных задач).

Видео:ЕГЭ 2024. ВСЁ ПРО ТРЕУГОЛЬНИКИ за 15 минутСкачать

Объём цилиндра

Материал для проведения самостоятельной работы.

🔥 Видео

ЗАДАНИЕ 1 ЕГЭ (ПРОФИЛЬ). РАВНОБЕДРЕННЫЕ ТРЕУГОЛЬНИКИ.Скачать

Треугольники №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

✓ Все сюжеты по планиметрии из ЕГЭ за 50 минут | ЕГЭ. Задание 16. Профильный уровень | Борис ТрушинСкачать

РЕШУ ЕГЭ. Планиметрия (ЕГЭ, задание 6): Решение прямоугольного треугольникаСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

ЗАДАНИЕ 1 ЕГЭ (ПРОФИЛЬ). РЕШЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.Скачать

Задачи на Треугольники Общего ВидаСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Стереометрия с нуля и до уровня ЕГЭ за 4 часа | Вся теория и задачи по №13 | Математика профильСкачать

1 задание ЕГЭ 2023 математики. Геометрия с нуляСкачать

Высота в прямоугольном треугольнике | Математика ЕГЭ 2024 #егэпрофиль #профильСкачать

Планиметрия 1 задание. ЕГЭ по математике 2024 | Аня МатеманяСкачать

#66. Задание 6: равнобедренный треугольникСкачать