Сколько существует различных треугольников (3 видео)

Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 40° и 70°?

Математика | 10 — 11 классы

Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 40° и 70°?

. так как третий угол треугольника = 70 градусов, то треугольник равнобедренный.

Следовательно, может быть, что 2 боковые стороны равны 1, либо основание равно 1.

Содержание

Сколько существует различных прямоугольников площади которых равны 12 квадратных см, а длины сторон выражены целым числом сантиметров?
Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целыми числами сантиметров?
Если две стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника то такие треугольники равны?
Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 50 и 60 градусов?
Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
Существует ли треугольник, если величина одного угла равна 25°, а другой угол в 3 раз( — а) больше?
Для треугольника ЕCP у которого равны углы C и Р?
Построй треугольник у которого одна сторона равна 7 см а два угла равны 40 градусов и 60 градусов?
Сколько существуют разных треугольников с целочисленными сторонами, периметр которых равны 15?
Сколько существует различных прямоугольников площади которых равны 20 см2 а длины сторон выраженны целым числом сантиметров?
Формула включений и исключений.
Сколько существует различных треугольников
💡 Видео

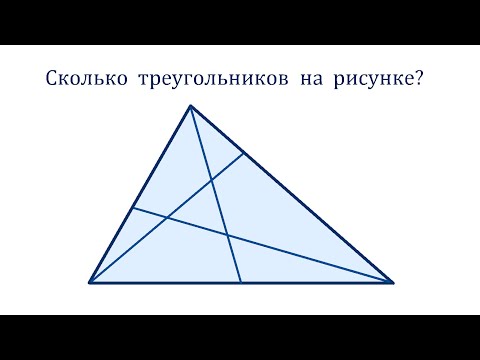
Видео:Сколько треугольников на рисунке?Скачать

Сколько существует различных прямоугольников площади которых равны 12 квадратных см, а длины сторон выражены целым числом сантиметров?

Сколько существует различных прямоугольников площади которых равны 12 квадратных см, а длины сторон выражены целым числом сантиметров?

Видео:Виды треугольниковСкачать

Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целыми числами сантиметров?

Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целыми числами сантиметров.

Видео:Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать

Если две стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника то такие треугольники равны?

Если две стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника то такие треугольники равны?

Видео:Виды треугольниковСкачать

Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 50 и 60 градусов?

Видео:Сколько треугольников на рисунке? Простая задача, которая позволяет загрузить даже студентовСкачать

Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?

Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?

Видео:Сколько треугольников на картинке? Расскажу, как посчитать это за 7 секунд!Скачать

Существует ли треугольник, если величина одного угла равна 25°, а другой угол в 3 раз( — а) больше?

Видео:СКОЛЬКО ТРЕУГОЛЬНИКОВ? 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Для треугольника ЕCP у которого равны углы C и Р?

Для треугольника ЕCP у которого равны углы C и Р.

Записатькакие стороны равны.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Построй треугольник у которого одна сторона равна 7 см а два угла равны 40 градусов и 60 градусов?

Построй треугольник у которого одна сторона равна 7 см а два угла равны 40 градусов и 60 градусов.

(постарайся найти не одно решение).

Видео:Разбор 9 задания | ОГЭ по информатике 2021Скачать

Сколько существуют разных треугольников с целочисленными сторонами, периметр которых равны 15?

Сколько существуют разных треугольников с целочисленными сторонами, периметр которых равны 15.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Сколько существует различных прямоугольников площади которых равны 20 см2 а длины сторон выраженны целым числом сантиметров?

Сколько существует различных прямоугольников площади которых равны 20 см2 а длины сторон выраженны целым числом сантиметров.

Перед вами страница с вопросом Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 40° и 70°?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Видео:Сколько треугольников вы видите на рисункеСкачать

Формула включений и исключений.

Пусть |Ω| — общее количество объектов, а |A_i| — количество объектов, которые обладают свойством i, |A 1∩ A 2 | — количество объектов, обладающих свойствами 1 и 2,…,|A₁∩…∩A_n| — количество объектов, обладающих свойствами 1,…,n. Тогда количество объектов, не обладающих ни одним из свойств равно:

Примеры решения задач

В летнем лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Решение:

Ответ: 10 ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

Сколько существует натуральных чисел, не превосходящих 1000, которые не делятся ни на 3, ни на 5?

Решение:

Натуральное число, которое делится на 3 можно представить в виде: 3·n, где n — натуральное число. Следовательно, 333 числа делятся на 3.

Натуральное число, которое делится на 5 можно представить в виде: 5·n, где n — натуральное число. Следовательно, 200 чисел делятся на 5.

Натуральное число, которое делится и на 3 и на 5 можно представить в виде: 15·n, где n — натуральное число. Следовательно, 66 чисел делятся на и на 3 и на 5.

Ответ: 533 числа не делятся ни на 3, ни на 5.

Сколько существует натуральных чисел, не превосходящих 1000, которые не делятся ни на 5, ни на 7?

Решение:

Натуральных чисел, которые делятся на 5: 200.

Натуральных чисел, которые делятся на 7: 142.

Числа, которые делятся и на 5 и на 7: 28.

Ответ: 686 чисел, не превосходящих 1000, не делятся ни на 5, ни на 7.

Каждая сторона в треугольнике ABC разделена на 8 равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки A, B, C не могут быть вершинами треугольников), у которых ни одна сторона не параллельна ни одной из сторон треугольника ABC?

Решение:

На каждой стороне треугольника 7 точек. Всего можно построить 7 3 треугольников. У 3·7 2 треугольников одна из сторон параллельна одной из сторон треугольника ABC, у 3·7 треугольников – две стороны, у 1 треугольника – все стороны.

7 3 -3·7 2 +3·7-1=343-147+21-1=216.

Ответ: 216 треугольников.

В классе 30 учеников. Сколькими способами они могут пересесть так, чтобы ни один не сел на своё место?

Решение:

Общее количество пересаживаний равно: 30!.

Количество пересаживаний, когда 1 ученик остается на своем месте равно: 29!·(30!/(30- 1 )!/ 1 !)=29!·30.

Количество пересаживаний, когда 2 ученика остаются на своем месте равно: 28!·30!/(30- 2 )!/ 2 !=28!·30·29/ 2 !

Количество пересаживаний, когда 29 учеников остаются на своем месте равно: 1!·30!/(30- 29 )!/ 29 !=30.

Количество пересаживаний, когда 30 учеников остаются на своем месте равно: 0!·30!/(30- 30 )!/ 30 !=1.

30!-29!30+28!·30·29/2!-…-30+1=30!(1-1/1!+1/2!-…-1/29!+1/30!)=30!(1/2!-…-1/29!+1/30!).

Ответ: 30!(1/2!-…-1/29!+1/30!).

Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Сколько существует различных треугольников

Представляем вниманию школьников 9-10 классов и их родителей возможность сверить свои задания с ответами к конкурсу «Кенгуру».
Вопросы сгруппированы по сложности (по баллам). Ответы на задания находятся после вопросов.

Задачи, оцениваемые в 3 балла

1. Бабочку отразили зеркально относительно прямой b, а потом повернули на 90° против часовой стрелки вокруг кончика носа кенгуру (точки А). После этого бабочка оказалась у кенгуру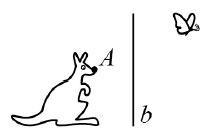

Варианты:
(А) на носу (Б) на лапе (В) на хвосте (Г) на спине (Д) в сумке

2. Сумма цифр семизначного числа равна 6. Чему равно произведение цифр этого числа?
Варианты:
(А) 0 (Б) 5 (В) 6 (Г) 7 (Д) невозможно определить

3. Сколько существует различных треугольников, у которых одна из сторон равна 1, а два угла равны 40° и 70°?
Варианты:
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 0

4. Сколько копеек в децисантикилорубле?
Варианты:
(А) 0,1 (Б) 1 (В) 10 (Г) 100 (Д) 1000

5. В Венеции каждый день происходит небольшое наводнение: вода поднимается, а потом отступает. На графике показано изменение уровня воды 6 мая 2011 года. Сколько часов в этот день уровень воды был выше 30 см?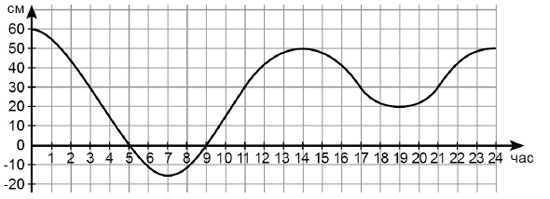

Варианты:
(А) 5 (Б) 6 (В) 7 (Г) 9 (Д) 12

6. Число, куб которого равен 2012 12 , умножили на квадрат числа 2012 11 . Что получилось?
Варианты:
(А) 2012 21 (Б) 2012 26 (В) 2012 31 (Г) 2012 58 (Д) 2012 88

7. Жук Жак ползёт по координатной плоскости. Он стартует из точки (1; 1) и движется так, что произведение его координат не меняется. По какой линии ползёт жук?
Варианты:
(А) по прямой (Б) по окружности (В) по параболе (Г) по гиперболе (Д) по ломаной линии

8. Часы лежат на столе циферблатом вверх. Минутная стрелка сейчас указывает на юго-восток. Через сколько минут она будет указывать на северо-восток?
Варианты:
(А) 15 (Б) 20 (В) 30 (Г) 40 (Д) 45

9. Как гласит русская поговорка, ложка дёгтя портит бочку мёда. Сколько банок мёда удастся испортить десятью каплями дёгтя, если в бочке 40 банок, а в ложке 200 капель?
Варианты:
(А) 2 (Б) 4 (В) 5 (Г) 10 (Д) 20

10. Про число х известно, что х 3 2 . Тогда
Варианты:
(А) 0 2 , и закрашенным параллелограммом. Чему равна площадь этого параллелограмма?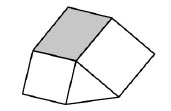

Варианты:
(А) 15 см 2 (Б) 16 см 2 (В) 18 см 2 (Г) 20 см 2 (Д) 21 см 2

12. Маша изучает натуральные числа, которые делятся на 72 и имеют в своей десятичной записи только нули и единицы. Сколько цифр в самом маленьком из таких чисел?
Варианты:
(А) 9 (Б) 11 (В) 12 (Г) 13 (Д) 14

13. В семье пятеро мужчин: Иван Сидорович, Сидор Иванович, Сидор Петрович, Пётр Сидорович и Пётр Петрович. Один из них сейчас смотрит в окно, его отец спит, брат читает книгу, а сыновья ушли гулять. Как зовут того, кто смотрит в окно?
Варианты:
(А) Иван Сидорович
(Б) Сидор Иванович
(В) Сидор Петрович
(Г) Пётр Сидорович
(Д) Пётр Петрович

14. Две стороны четырёхугольника равны 1 и 7. Одна из диагоналей, длина которой равна 3, делит его на два равнобедренных треугольника. Чему равен периметр этого четырёхугольника?
Варианты:
(А) 12 (Б) 14 (В) 16 (Г) 18 (Д) 20

15. Натуральные числа а и b таковы, что a + b = 2012. Какое из следующих равенств возможно при некотором натуральном k ?
Варианты:

16. Число х отрицательно, а число у положительно. Что не может произойти, если х увеличить, а у — уменьшить?
Варианты:
(А) х + у увеличится (Б) x/y уменьшится (В) y/x уменьшится (Г) у — х уменьшится (Д) x-y уменьшится

17. На какое наименьшее число тупоугольных треугольников можно разрезать квадрат?
Варианты:
(А) 4 (Б) 5 (В) 6 (Г) 7 (Д) это невозможно сделать

18. Какое из утверждений А-Г неверно?
Варианты:
(A) произведение любых двух нечётных чисел — нечётное число
(Б) произведение любых двух нечётных функций — нечётная функция
(B) произведение любых двух чётных чисел — чётное число
(Г) произведение любых двух чётных функций — чётная функция
(Д) все утверждения А-Г верны

19. В некоторых клетках таблицы 10×10 поставлены крестики так, что каждый из них — единственный либо в своей строке, либо в своём столбце. Какое наибольшее число крестиков может быть в такой таблице?
Варианты:
(А) 10 (Б) 15 (В) 18 (Г) 19 (Д) 99

20. Разность корней квадратного уравнения х 2 + bх + с = 0 — чётное число. Чему может равняться ордината вершины параболы у = х 2 +bx + c ?
Варианты:
(А)-2 (Б) -3 (В)-4 (Г) -5 (Д)-6

Задачи, оцениваемые в 5 баллов

21. Винни-Пух пошёл в магазин за мёдом. Цена одного горшочка — 1 фунт, но при покупке n горшочков (n 2 * 3 3 * 5 и 2 3 * 3, а каждое из чисел 2 5 * 3 7 * 5 3 и 2 4 * 3 6 * 5 2 делится на m и n. Чему равно наибольшее возможное отношение чисел m и n ?

Варианты:
(А) 2 2 * 3 4 * 5 2
(Б) 2 * З 3
(В) 2 2 * 3 3 * 5 2
(Г) 2 * 3 2 * 5
(Д) 2 * 3 3 * 5

24. Правильный треугольник «катится» вокруг квадрата (см. рисунок) Какую траекторию опишет отмеченная точка, прежде чем и она, и весь треугольник вернутся в исходное положение?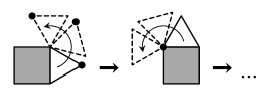

Варианты:

25. Дробь 28/33 хотят представить в виде суммы нескольких дробей, числители
которых равны 1. При каком наименьшем числе слагаемых это возможно?
Варианты:
(А) 2 (Б) 3 (В) 4 (Г) 5 (Д) 28

26. На плоскости нарисовано несколько прямых. Рядом с каждой прямой написано число прямых, которые ее пересекают. Среди написанных чисел имеется не менее четырёх различных, два из которых — это 6 и 7. Сколько прямых нарисовано?
Варианты:
(А) 9 (Б) 10 (В) 13 (Г) 15 (Д) невозможно определить

27. В треугольнике длины сторон равны а, b и с, а угол, лежащий против стороны b, вдвое больше угла, лежащего против стороны а. Тогда обязательно
Варианты:
(А) а 2 + с 2 = b 2
(Б) b 2 + bс = а 2
(В) c 2 + ab = a 2
(Г) а 2 + ас = b 2
(Д) каждое из соотношений А-Г может быть нарушено

28. На рисунке ОА = 6 см, ОВ= 4 см. Каково множество всех точек Р, лежащих в первой четверти, для которых площадь четырёхугольника ОБ равна 24 см 2 ?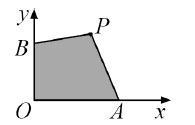

Варианты:

29. Назовём тройку различных чисел, выбранных из множества , хорошей, если никакая пара чисел из этой тройки не имеет сумму 7. Коля перемножил числа в каждой хорошей тройке, а потом сложил полученные произведения. Какое число он получил?
Варианты:
(А) 7 2 (Б) 7 3 (В) З 6 (Г) 3 7 (Д) 6 3

30. Из 27 одинаковых маленьких кубиков сложили куб. Через середину его диагонали провели плоскость, перпендикулярную этой диагонали. Сколько маленьких кубиков пересекла эта плоскость?
Варианты:
(А) 17 (Б) 18 (В) 19 (Г) 20 (Д) 21