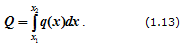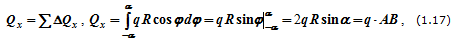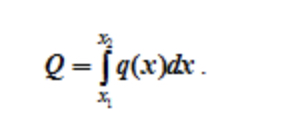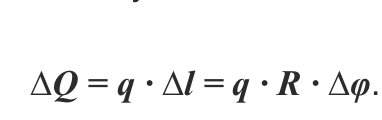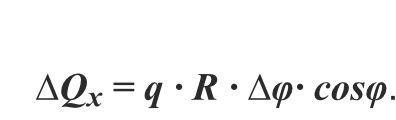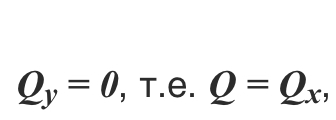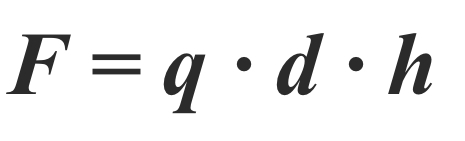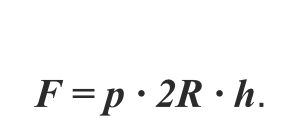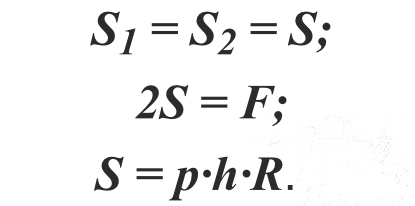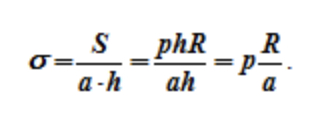Равномерно распределенная нагрузка треугольник (2 видео)

Сопромат online

Содержание

Расчеты в режиме online
1.5. Треугольная распределенная нагрузка
iSopromat.ru
Решение задач, контрольных и РГР
Набор студента для учёбы
Распределенная нагрузка на балку — формулы, условия и примеры расчета
Равномерно и неравномерно распределенная нагрузка на балку
Пример решения задач с распределенной нагрузкой
🔥 Видео

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Расчеты в режиме online

Видео:Распределенная нагрузкаСкачать

1.5. Треугольная распределенная нагрузка

Построить эпюры поперечных сил и изгибающих моментов для балки, нагруженной распределенной по закону треугольника нагрузкой, если величина максимальной интенсивности нагрузки равна p₀ = 20 кН/м (рис. 1.13).

Решение. Определим опорные реакции балки, для чего заменим распределенную нагрузку сосредоточенной силой Fc, приложенной в центре тяжести треугольника и равной его площади:

Составим уравнения моментов относительно опор В и D:

Проведем от опоры В на расстоянии х₁ сечение и составим выражения для Q_x и М_х , для чего найдем величину интенсивности нагрузки в сечении х₁ . Из подобия треугольников получим:

Заменим треугольную нагрузку на длине х₁ равнодействующей силой F_x, приложенной в центре тяжести треугольника:

I участок: 0 ≤ х₁ ≤ 2,4 м ;

Из уравнений Q_x и М_х следует, что эпюра Q_x представляет квадратичную параболу, а эпюра М_х — кубическую.

Подставив числовые значения x₁ на границах участка, получим

Так как поперечная сила пересекает ось х, найдем координату поперечного сечения, в котором Q равна нулю, а изгибающий момент имеет максимальное значение:

По вычисленным данным, в соответствии с правилами построения эпюр, строим эпюры Q и M на первом участке.

II участок: 0 ≤ х₂ ≤ 2,4 м ;

Из эпюр следует, что максимальное значение изгибающий момент имеет в сечении, в котором поперечная сила равна нулю, М_max = 14,8 кН*м.

Видео:Эпюры изгибающего момента и поперечной силы от треугольной распределенной нагрузкиСкачать

iSopromat.ru

Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены не в одной точке твердого тела (т.е. не сосредоточены в одной точке), а равномерно, случайным образом или по заданному закону распределены по его определенной длине, площади или объему.

Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.

Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м 2 , для объемной (например при учете собственного веса элементов конструкции) — Н/м 3 .

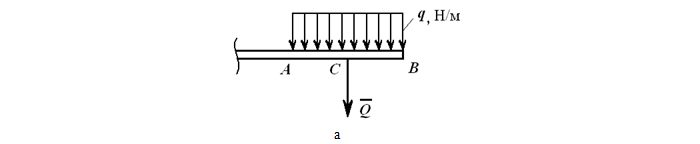
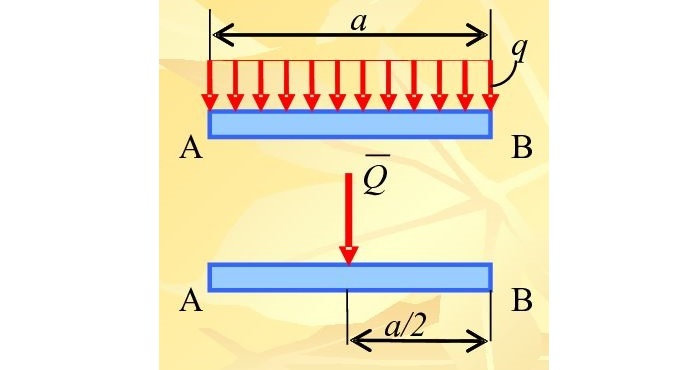
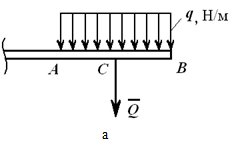
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой

приложенной в середине отрезка AB.

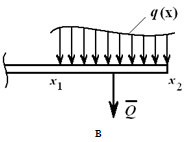
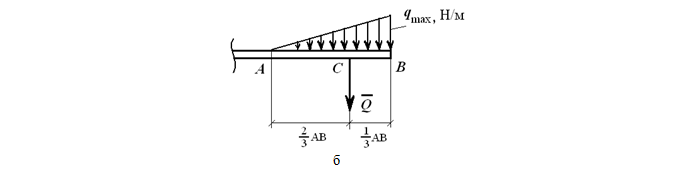
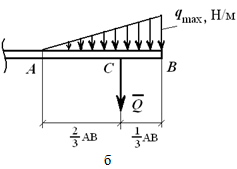
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой

приложенной в точке C, причем AC = 2/3AB.

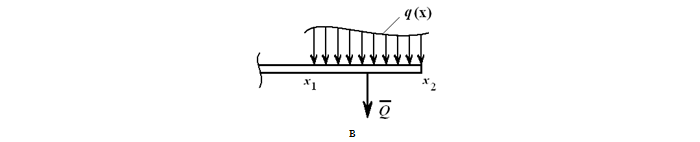
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу

Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).

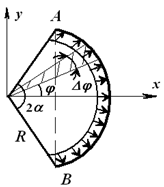
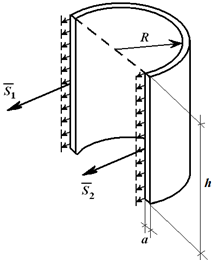
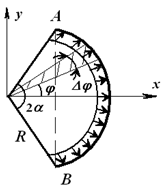
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).

Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:

В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:

где АВ – хорда, стягивающая концы дуги.

Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м, 2 ]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h ( d – внутренний диаметр) или

Разрывающие баллон по диаметру усилия:

Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Построение эпюр в балке с треугольной нагрузкой / строительная механикаСкачать

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Видео:Преобразование равномерно распределенной нагрузки.Скачать

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Видео:Определение реакций опор в балке. Сопромат.Скачать

Распределенная нагрузка на балку — формулы, условия и примеры расчета

Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.

Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м 3 ] для объемной конструкции, в [H/м 2 ] — для площади, для линейной – в [H/м].

Продемонстрируем это на рисунке:

Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:

здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].

Примечательно, что сила приложена к середине данного отрезка AB.

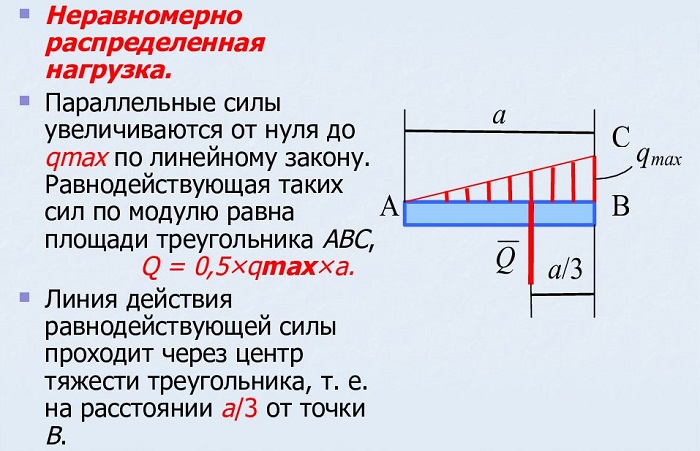
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:

где q_max – максимальная интенсивность [Н/м].

Q приложена к точке C, где AC равно: AC = 2/3 AB

Рассматривая функцию q(x), представленную на рисунке:

можно высчитать значение эквивалентной силы по формуле:

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Равномерно и неравномерно распределенная нагрузка на балку

Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а.

Единицы измерения распределённой нагрузки [Н/м].

Её также можно заменить на величину Q, которая приложена в середину AB.

Составим формулу: Q = q∗a

Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.

При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.

Видео:Балка с линейно распределенной нагрузкойСкачать

Пример решения задач с распределенной нагрузкой

Рассмотрим пример распределенной нагрузки на балку. Им может послужить тяга, благодаря которой происходит разрыв стальной стенки баллона с некоторым газом.

Для начала определяем результирующую давления в металлической трубе. Интенсивность равна q, радиус этого сектора трубы – R, ось симметрии Оx, а 2α – это центральный угол. Представим это на рисунке:

Выделим элемент сектора трубы ∆ϕ.

Затем определим единицу силы ∆Q. Она действует на плоскость дуги. Составим формулу:

Проекция результирующей тяги на ось Оx является:

Исходя из вышесказанного, можно найти проекцию этой же силы на ось Оy:

AB является хордой, которая стягивает дугу.

В нашей задаче сосуд – это ёмкость цилиндрической формы с высотой H, внутренним давлением P, действующим на стенки, и нагрузкой q = p [Н/м 2 ].

Разделим цилиндр вдоль его диаметра.

Исходя из этого, равнодействующая результирующих сил определяется по формуле:

где d – это внутренний диаметр цилиндра, h — его высота.

Формулу также можно записать следующим образом:

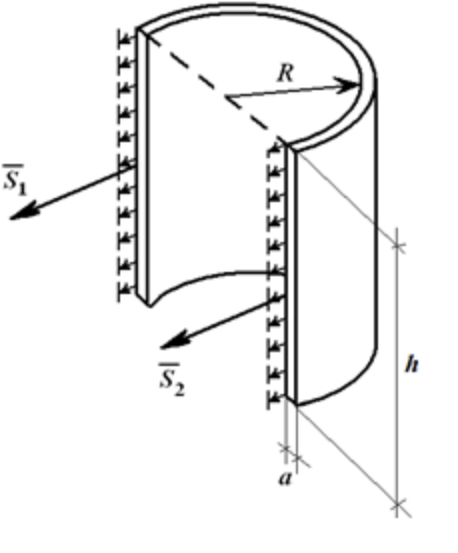
Итак, почему баллон имеет способность разрываться? На его стенки действуют значения S1, S2, S3 (площади), а также F, p (плотность), h (высота цилиндра) и R (его радиус). Рассчитаем их по формулам:

Изобразим баллон в момент разрыва:

Учтём a – толщину ёмкости. Таким образом напряжение, которое растягивает баллон, (усилия распространяются в том числе на крышку и дно цилиндра) равно:

Важную роль при решении практических задач также играет эпюра распределенной нагрузки – плоская фигура, которая ограничена графиком. Величина, действующая на балку, называется интенсивностью – силой, которая распространяется на единицы площади, объема или длины.