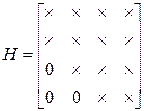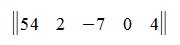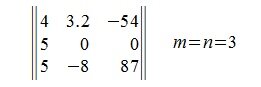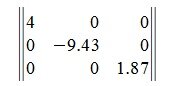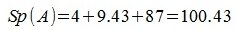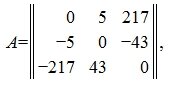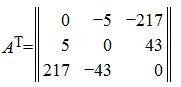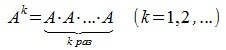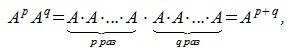Правый верхний треугольник матрицы

Квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю, называется треугольной. Треугольная матрица может быть верхнего и нижнего строения. Верхняя и нижняя формы имеют соответственно вид:

, .

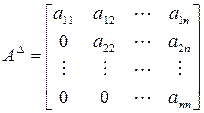
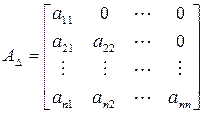
Треугольные матрицы обладают рядом важных в практическом отношении свойств:

1) Определитель треугольной матрицы равен произведению ее диагональных элементов:

.

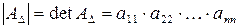
Следовательно, треугольная матрица является неособенной только тогда, когда все элементы ее главной диагонали отличны от нуля.

2) Сумма и произведение треугольных матриц одинакового строения есть также треугольная матрица того же строения.

3) Неособенная треугольная матрица легко обращается, и ее обратная матрица снова имеет треугольную структуру того же строения.

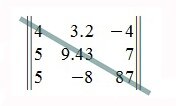
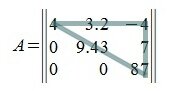
4) Всякая неособенная матрица при помощи элементарных преобразований только над строками или только над столбцами может быть приведена к треугольной матрице. В качестве примера рассмотрим известную в теории устойчивости матрицу Гурвица

.

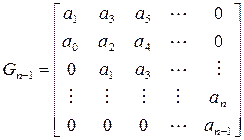
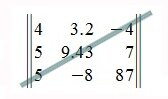
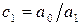
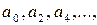
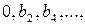
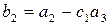
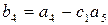
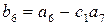
Для перехода к верхнему треугольному виду проделаем следующие элементарные преобразования. Из каждого элемента второй строки вычтем стоящий над ним элемент первой строки, предварительно умноженный на . Вместо строки с элементами получим строку с элементами где , , , . и т. д.

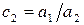
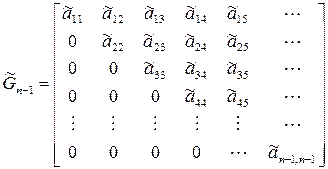
Выполним аналогичные операции в остальных нижележащих строках. Затем вычтем из каждого элемента третьей строки преобразованной матрицы стоящие над ней элементы строки, умноженные на , и повторим аналогичные операции в остальных строках. Продолжим процесс по этой процедуре до тех пор, пока на m-м шаге не получим верхнюю треугольную матрицу

.

Такие преобразования по существу эквивалентны умножению матрицы справа (или слева) на некоторую другую вспомогательную матрицу.

Определитель матрицы Гурвица

.

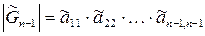
Существует теорема о разложении любой квадратной матрицы в произведение двух треугольных. Согласно этой теореме, всякая квадратная матрица может быть представлена в виде произведения нижней и верхней треугольных матриц:

,

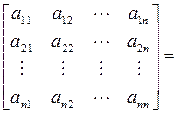
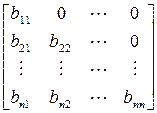
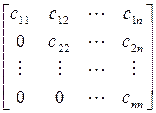
при условии, что ее диагональные миноры отличны от нуля:

, , .

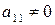
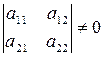
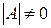
Это разложение является единственным, если зафиксировать диагональные элементы одной из треугольных матриц (например, положить их равными единице). Разложение любой квадратной матрицы в произведение двух треугольных с предписанными диагональными элементами широко используется в вычислительных методах при решении задач с помощью ЭВМ.

Однозначное представление матрицы в виде произведения двух треугольных может быть обобщено на клеточные матрицы. В таких матрицах сами элементы являются матрицами. При этом матрица может быть разложена в произведение нижней и верхней квазитреугольных матриц.

Определитель квазитреугольной матрицы равен произведению ее диагональных клеток.

В отличие от диагональных матриц операция умножения треугольных матриц в общем случае не коммутативна.

В вычислительных методах теории управления существенную роль играют не только треугольные, но и так называемые почти треугольные матрицы. Многие методы используют разложение матрицы в виде произведения двух матриц, одна из которых имеет треугольное строение. Матрица А называется правой (левой) почти треугольной или матрицей Хессенберга, если для ее элементов а_ij выполняются соотношения:

; ; .

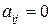
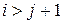
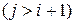
Например, матрица Хессенберга правой почти треугольной формы размерности (4×4) имеет вид

Отметим полезные особенности рассматриваемых матриц, которые используются в вычислительных методах:

а) сумма почти треугольных матриц одинакового строения будет треугольной матрицей того же строения, а произведение — нет;

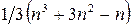
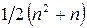
б) построение характеристического полинома почти треугольных матриц экономично, так как требует гораздо меньшего объема вычислений, чем при произвольной форме матрицы. Число операций умножений составляет , сложений — ;

в) почти треугольная матрица может быть разложена в произведение двух треугольных, причем в разложении одна из матриц будет иметь более простую структуру, а именно, будет двухдиагональной.

В современных инженерных методах, заложенных в системы автоматизированного проектирования, широко используется мультипликативное представление матриц, например, QR-представление. Его сущность состоит в том, что любую квадратную матрицу А можно представить в виде произведения ортогональной и почти треугольной форм

, или , (4.4)

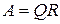
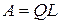
где Q — ортогональная матрица; R — правая (верхняя) треугольная форма; L — левая (нижняя) треугольная форма матрицы.

Представление (4.4) называется QR-разложением (в случае нижней треугольной матрицы QL-разложением) и для матрицы А является единственным.

QR- и QL-алгоритмы принципиально мало различаются. Их использование зависит от того, как расположены элементы матрицы. Если они сосредоточены в нижнем правом углу, эффективнее использовать QL-алгоритм. Если элементы матрицы сосредоточены в левой верхней части, то целесообразнее использовать QR-алгоритм. При правильной реализации на ЭВМ ошибки округления во многих случаях не оказывают большого влияния на точность вычисления.

Дата добавления: 2014-12-27 ; просмотров: 6286 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Введение в матричные типы в линейной алгебре для машинного обучения

Дата публикации 2018-02-09

Много линейной алгебры связано с операциями над векторами и матрицами, и есть много различных типов матриц.

Есть несколько типов матриц, с которыми вы можете столкнуться снова и снова, когда начинаете изучать линейную алгебру, в частности части линейной алгебры, относящиеся к машинному обучению.

В этом уроке вы обнаружите набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться при машинном обучении.

После завершения этого урока вы узнаете:

• Квадратные, симметричные, треугольные и диагональные матрицы, которые соответствуют их названиям.
• Все матрицы идентичности имеют нулевые значения, кроме главной диагонали, где значения равны 1.
• Ортогональные матрицы, которые обобщают идею перпендикулярных векторов и имеют полезные вычислительные свойства.

• Обновление февраль / 2018: Исправлена ​​небольшая опечатка в уравнении эквивалентности для ортогональной матрицы.

Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Обзор учебника

Этот урок разделен на 6 частей, чтобы охватить основные типы матриц; они есть:

1. Квадратная матрица
2. Симметричная матрица
3. Треугольная матрица
4. Диагональная матрица
5. Единичная матрица
6. Ортогональная матрица

Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Квадратная матрица

Квадратная матрица — это матрица, в которой количество строк (n) равно количеству столбцов (m).

Квадратная матрица контрастирует с прямоугольной матрицей, где количество строк и столбцов не равно.

Учитывая, что количество строк и столбцов совпадают, размеры обычно обозначаются как n, например, п х н. Размер матрицы называется порядком, поэтому квадратная матрица порядка 4 имеет размер 4 x 4.

Вектор значений по диагонали матрицы от левого верхнего до правого нижнего угла называется главной диагональю.

Ниже приведен пример квадратной матрицы порядка 3.

Квадратные матрицы легко складываются и умножаются вместе и являются основой многих простых линейных преобразований, таких как вращения (как в поворотах изображений).

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Симметричная матрица

Симметричная матрица — это тип квадратной матрицы, в которой верхний правый треугольник совпадает с нижним левым треугольником.

Не будет преувеличением сказать, что симметричные матрицы S являются наиболее важными матрицами, которые мир когда-либо увидит — в теории линейной алгебры, а также в приложениях.

Чтобы быть симметричным, ось симметрии всегда является главной диагональю матрицы, слева направо и снизу справа.

Ниже приведен пример симметричной матрицы 5 × 5.

Симметричная матрица всегда квадратная и равна ее собственной транспонировании.

Видео:Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Треугольная матрица

Треугольная матрица — это тип квадратной матрицы, в которой все значения находятся в верхнем правом или нижнем левом углу матрицы, а остальные элементы заполнены нулевыми значениями.

Треугольная матрица со значениями только выше главной диагонали называется верхней треугольной матрицей. Принимая во внимание, что треугольная матрица со значениями только ниже основной диагонали называется нижней треугольной матрицей.

Ниже приведен пример верхней треугольной матрицы 3 × 3.

Ниже приведен пример нижней треугольной матрицы 3 × 3.

Разложение LU разрешает данную матрицу в верхнюю и нижнюю треугольные матрицы.

NumPy предоставляет функции для вычисления треугольной матрицы из существующей квадратной матрицы. Функция tril () для вычисления нижней треугольной матрицы по заданной матрице и функция triu () для вычисления верхней треугольной матрицы по заданной матрице

Пример ниже определяет квадратную матрицу 3 × 3 и вычисляет нижнюю и верхнюю треугольную матрицу из нее.

При выполнении примера печатается определенная матрица, за которой следуют нижняя и верхняя треугольные матрицы.

Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Диагональная матрица

Диагональная матрица — это матрица, в которой значения вне главной диагонали имеют нулевое значение, а главная диагональ берется из верхнего левого угла матрицы в правый нижний угол.

Диагональная матрица часто обозначается переменной D и может быть представлена ​​в виде полной матрицы или вектора значений на главной диагонали.

Диагональные матрицы состоят в основном из нулей и имеют ненулевые элементы только вдоль главной диагонали.

Ниже приведен пример квадратной диагональной матрицы 3 × 3.

Как вектор, он будет представлен как:

Или с указанными скалярными значениями:

Диагональная матрица не обязательно должна быть квадратной. В случае прямоугольной матрицы диагональ будет охватывать кратчайшее измерение; например:

NumPy предоставляет функцию diag (), которая может создать диагональную матрицу из существующей матрицы или преобразовать вектор в диагональную матрицу.

В приведенном ниже примере определяется квадратная матрица 3 × 3, извлекается главная диагональ в виде вектора, а затем создается диагональная матрица из извлеченного вектора.

При выполнении примера сначала печатается определенная матрица, за которой следует вектор главной диагонали и диагональная матрица, построенная из вектора.

Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Единичная матрица

Тождественная матрица — это квадратная матрица, которая не меняет вектор при умножении.

Значения единичной матрицы известны. Все скалярные значения вдоль главной диагонали (сверху-слева-внизу-справа) имеют значение один, а все остальные значения равны нулю.

Тождественная матрица — это матрица, которая не меняет вектор, когда мы умножаем этот вектор на эту матрицу.

Тождественная матрица часто представляется с использованием обозначения «I» или с размерностью «In», где n — индекс, который указывает размерность квадратной единичной матрицы. В некоторых обозначениях тождество может упоминаться как единичная матрица или «U», чтобы соответствовать одному значению, которое оно содержит (это отличается от унитарной матрицы).

Например, единичная матрица размером 3 или I3 будет выглядеть следующим образом:

В NumPy матрица идентичности может быть создана с определенным размером, используя функцию identity ().

В приведенном ниже примере создается единичная матрица I3.

При выполнении примера печатается созданная единичная матрица.

В одиночку единичная матрица не так интересна, хотя она является компонентом других операций импорта матрицы, таких как инверсия матрицы.

Видео:Приведение определителя к треугольному видуСкачать

Ортогональная матрица

Два вектора ортогональны, когда их скалярное произведение равно нулю, и называется ортонормированным.

Это интуитивно понятно, если учесть, что одна линия ортогональна другой, если она перпендикулярна ей.

Ортогональная матрица — это тип квадратной матрицы, столбцы и строки которой представляют собой ортонормированные единичные векторы, например, перпендикулярно и имеет длину или величину 1.

Ортогональная матрица — это квадратная матрица, строки которой взаимно ортонормированы, а столбцы взаимно ортонормированы

Ортогональная матрица часто обозначается заглавной буквой «Q».

Умножение на ортогональную матрицу сохраняет длины.

Ортогональная матрица формально определяется следующим образом:

Где Q — ортогональная матрица, Q ^ T обозначает транспонирование Q, а I — единичная матрица.

Матрица ортогональна, если ее транспонирование равно обратному.

Другая эквивалентность для ортогональной матрицы состоит в том, если скалярное произведение матрицы само по себе равно единичной матрице.

Ортогональные матрицы часто используются для линейных преобразований, таких как отражения и перестановки.

Ниже приведена простая ортогональная матрица 2 × 2, которая является примером матрицы отражения или координатного отражения.

Пример ниже создает эту ортогональную матрицу и проверяет вышеуказанные эквивалентности.

Выполнение примера сначала печатает ортогональную матрицу, инверсию ортогональной матрицы и транспонирование ортогональной матрицы затем печатают и показывают, что они эквивалентны. Наконец, печатается единичная матрица, которая вычисляется из точечного произведения ортогональной матрицы с ее транспонированием.

Ортогональные матрицы являются полезными инструментами, поскольку они дешевы в вычислительном отношении и стабильны, чтобы вычислять их обратные значения как просто их транспонирование.

Видео:Как вычислить определитель матрицы четвертого порядка | Высшая математикаСкачать

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Модифицируйте каждый пример, используя свои собственные маленькие надуманные данные.
• Напишите свои собственные функции для реализации каждой операции.
• Исследуйте один пример, где каждая операция использовалась в машинном обучении.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Видео:Обратная матрицаСкачать

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Раздел 6.2. Специальные типы матриц.Руководство по линейной алгебре, 2017
• Введение в линейную алгебру, 2016
• Раздел 2.3. Идентичность и обратные матрицы,Глубокое обучение, 2016
• Раздел 2.6. Специальные виды матриц и векторов,Глубокое обучение, 2016

статьи

Видео:Аржанцев И. В. - Алгебра. Часть 1 - ОпределителиСкачать

Резюме

В этом уроке вы обнаружили набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться при машинном обучении.

В частности, вы узнали:

• Квадратные, симметричные, треугольные и диагональные матрицы, которые соответствуют их названию.
• Матрицы идентичности, которые являются нулевыми значениями, кроме главной диагонали, где значения равны 1
• Ортогональные матрицы, которые обобщают идею перпендикулярных векторов и имеют полезные вычислительные свойства.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Видео:Определитель матрицы и все способы его найтиСкачать

Матрица столбец

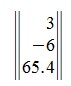
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Видео:Обратная матрица (2 способа нахождения)Скачать

Нулевая матрица

Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например

Видео:Для чего матрицы в жизни? | Высшая математика | TutorOnlineСкачать

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Видео:Как найти ранг матрицы (пример) - bezbotvyСкачать

Главная диагональ матрицы

Элементы расположенные на местах a 11, a 22 . a_nn образуют главную диагональ матрицы. Например:

В случае m×n -матриц элементы a_ii ( i= 1,2. min(m,n)) также образуют главную диагональ. Например:

Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .

Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Побочная диагональ матрицы

Элементы расположенные на местах a 1n, a 2n-1 . a n1 образуют побочную диагональ матрицы. Например:

Видео:4. Что такое определитель матрицы? - bezbotvyСкачать

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Видео:Вычислить определитель путём накопления нулей в строке или столбцеСкачать

Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n , где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

Верхняя треугольная матрица

Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j . Например:

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство: