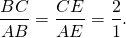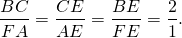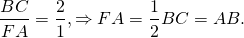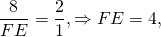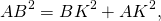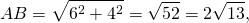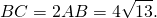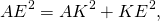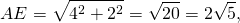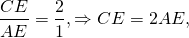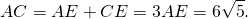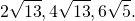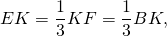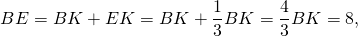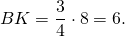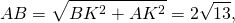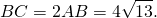Перпендикулярные биссектрисы в треугольнике (3 видео)

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Содержание

Определение биссектрисы угла треугольника
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Пример задачи
В треугольнике биссектриса и медиана перпендикулярны
Существует ли треугольник, две биссектрисы которого перпендикулярны?
Ваш ответ
решение вопроса
Похожие вопросы
🔥 Видео

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Построение биссектрисы в треугольникеСкачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Видео:25 задание ОГЭ ✧ В ∆ABC биссектриса BE и медиана AD перпендикулярны и ... #огэ #егэ #геометрияСкачать

В треугольнике биссектриса и медиана перпендикулярны

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.

Найти стороны треугольника ABC.

Дано: ΔABC,

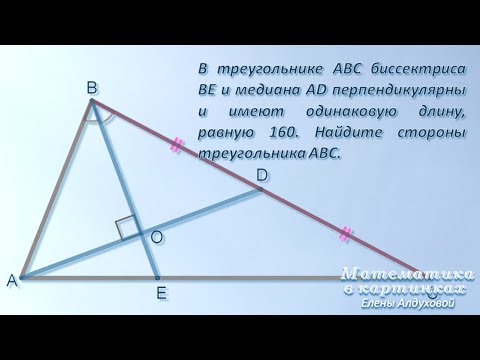
AD — медиана, BE — биссектриса,

Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD. Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

3) По свойству биссектрисы треугольника в ΔABC

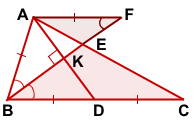
3) Проведём через точку A прямую, параллельную BC и продлим BE до пересечения с этой прямой в точке F.

Рассмотрим треугольники BEC и FEA.

∠AFB=∠CBF (как внутренние накрест лежащие при BC || AF и секущей BF).

Значит треугольники BEC и FEA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Таким образом, треугольник ABF — равнобедренный с основанием BF, а значит, его высота AK является также медианой и BK=KF.

4) Рассмотрим прямоугольный треугольник ABK. По теореме Пифагора

5) Рассмотрим прямоугольный треугольник AKE.

KE=BE-BK=8-6=2. По теореме Пифагора

1) Пусть AD∩BE=K.

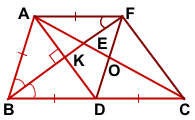
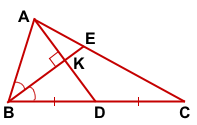
Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

2) Отложим на луче BE с другой стороны от точки K отрезок KF, KF=BK.

Проведём отрезки DF и CF.

Четырёхугольники AFDB и AFCD — параллелограммы (по признаку параллелограмма). Тогда AF=BD, DF=AB, FC=AD (по свойству параллелограмма), а так как AB=BD, то ABCD — ромб.

AC∩DF=O. По свойству параллелограмма O — середина DF. Значит E — точка пересечения медиан треугольника AFD. По свойству медиан FE:EK=2:1. Следовательно