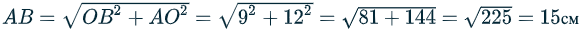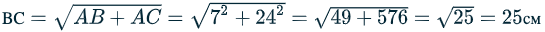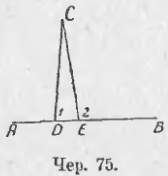Содержание:
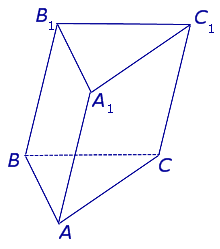
Призмой зовётся объёмный многогранник, состоящий из двух одинаковых основ – многоугольников, расположенных в перпендикулярных плоскостях. Её боковые грани – прямоугольники или параллелограммы, имеют с ними общие грани. Наклонная призма – геометрическое тело с рёбрами, расположенными к основаниям под углом, отличным от прямого. Её верхняя и нижняя плоскости остаются параллельными.
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Разновидности
Полная поверхность – сумма боковых поверхностей, нижней и верхней. Боковая – представлена параллелограммами. Расстояние между плоскостями оснований зовётся высотой геометрического тела.
Наклонная трехгранная или треугольная призма представлена пятигранником с равными основаниями в виде треугольников, которые смещены друг относительно друга. Боковые ребра наклонены к основанию.
Объём вычисляется по классической формуле:
Полная площадь: S = Sбок + 2Sосн или Pоснh + 2Sосн.
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Сечения
Сечением тела называется фигура, представленная всеми его точками, расположенными на плоскости α. Перпендикулярное сечение наклонной призмы пересекает её боковые рёбра под углом 90°.
- Перпендикулярные сечения геометрического тела равны один другому.
- Сечение будет перпендикулярным боковым ребрам.
Если под углом 90° к боковым граням проходит плоскость сечения, геометрическая фигура называется усечённой. Периметр перпендикулярного сечения такой призмы равен:
- P – периметр фигуры сечения;
- l – боковое ребро, например, dD.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Задача
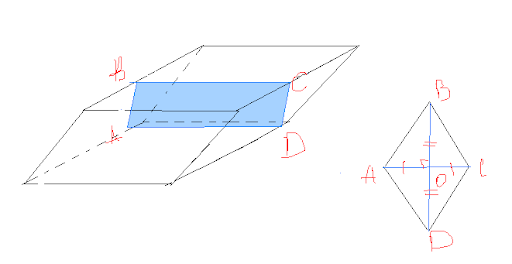
Перпендикулярным сечением наклонной четырехугольной призмы является ромб с диагоналями BD = 24 см, AC = 18 см. Боковая поверхность – 780 см2. Вычислить боковое ребро геометрической фигуры.
Начнём с рассмотрения перпендикулярного сечения. Стороной призмы является высота пересекающей плоскости. Сторона ромба вычисляется благодаря прямоугольному треугольнику AOB, где катеты равны половине диагонали (особенность рассматриваемого многоугольника).
Половины диагоналей OB и AO равны 9 и 12 см.
Воспользуемся теоремой Пифагора:
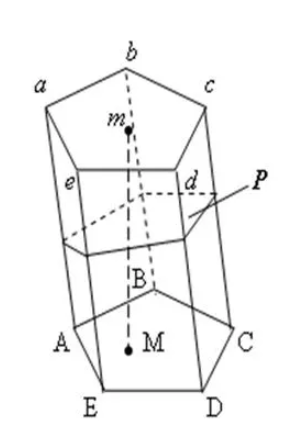
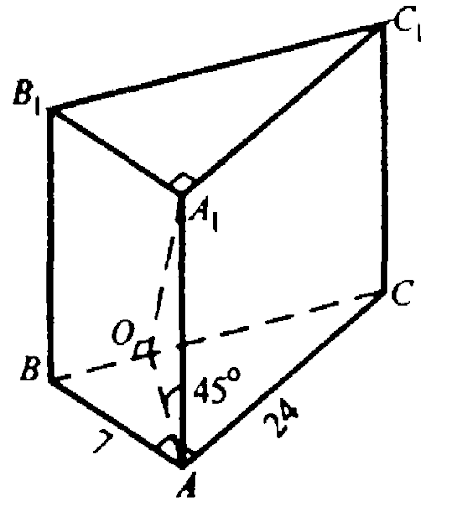
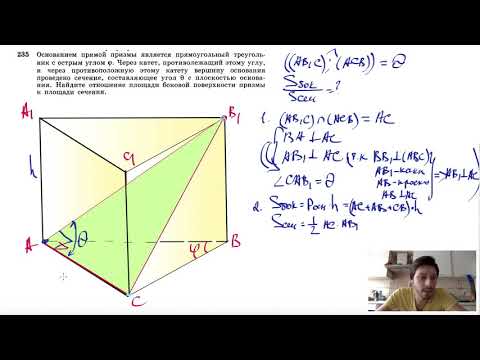
Дана наклонная призма, в основании которой лежит прямоугольный треугольник. Катеты равны 7 и 24 см. Вершина A1 находится на одинаковом удалении от вершин треугольника. Вычислить высоту призмы, где ребро AA1 находится под углом 45° к основанию.
Проекция точки A1 на сторону BC △АВС представлена точкой O – это центр окружности, описанной вокруг нижнего основания △АВС. Отсюда следует: O делит гипотенузу ВС на равные отрезки BO = OC. Причём BC ⊥ А1О – высота геометрического тела.
ΔА1ОА является равнобедренным прямоугольным, а отрезки А1О и АО равны.
Воспользуемся теоремой Пифагора.
Расстояния от вершин до точки O равны 25 : 2 = 12,5 см.
Видео:№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Сечения призмы. Перпендикулярные сечения призмы
 Сечения призмы Сечения призмы |
 Перпендикулярные сечения призмы Перпендикулярные сечения призмы |
Видео:Как строить сеченияСкачать

Сечения призмы
Определение 1. Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости α .
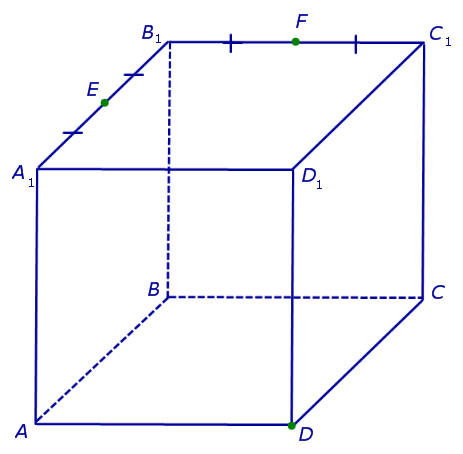
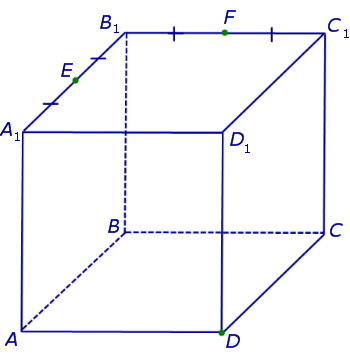
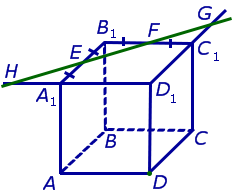
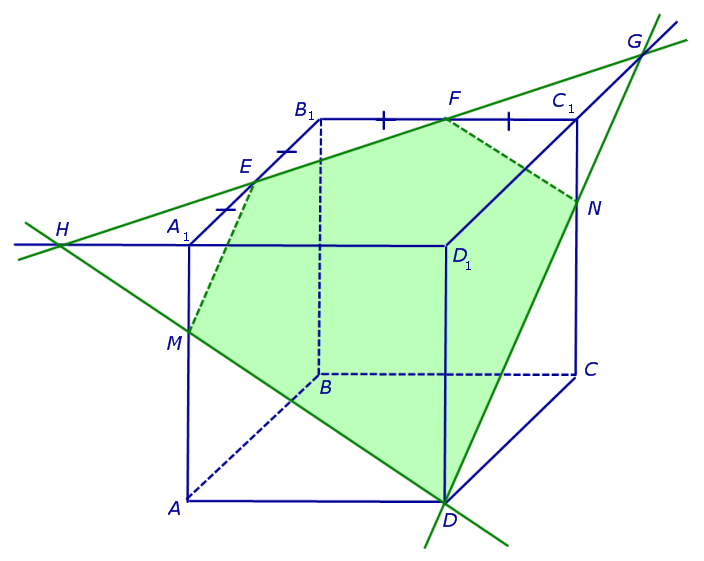
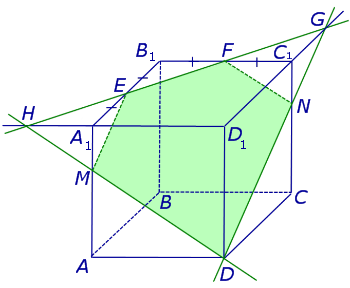
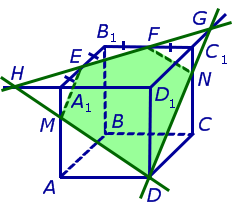
В качестве примера рассмотрим сечение куба куба ABCDA1B1C1D1 плоскостью, проходящей через точку D и середины ребер A1B1 и B1C1 . Рассмотрим процесс построения сечения подробно.
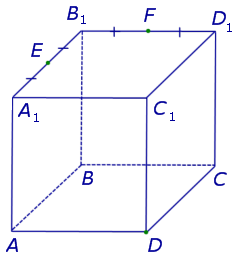
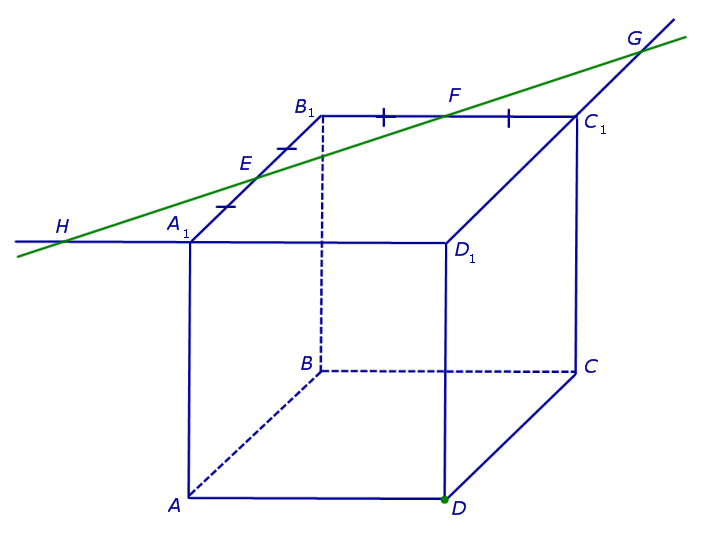
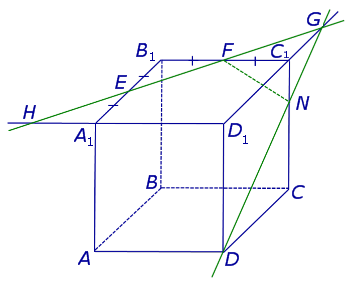
Поскольку точки E и F лежат на ребрах одной грани куба A1B1C1D1 , то проведем прямую EF до пересечения с продолжениями двух других ребер этой грани. Обозначим буквой G точку пересечения прямой EF с продолжением отрезка D1C1 за точку C1 , а буквой Н – точку пересечения прямой EF с продолжением отрезка D1A1 за точку A1 . Эти точки пересечения существуют, поскольку все указанные прямые лежат в одной плоскости A1B1C1D1 и не параллельны параллельны попарно (рис. 2).
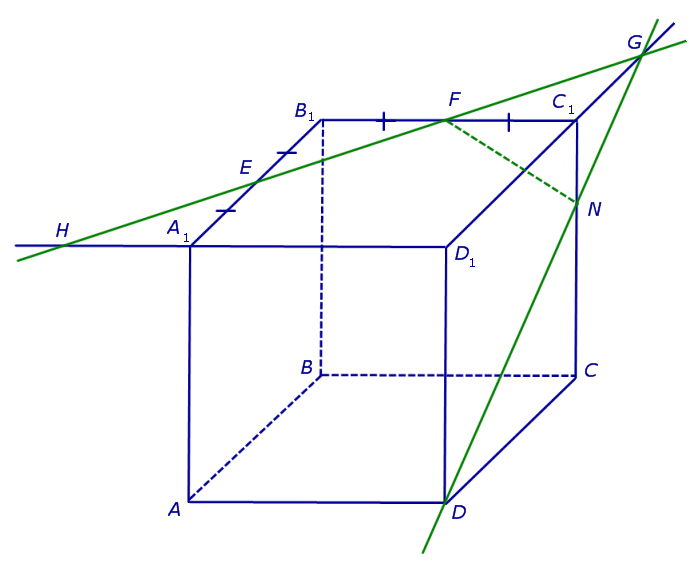
Точки G и D принадлежат плоскости сечения, а, значит, и вся прямая DG лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба DD1C1C . Значит, точка пересечения DG с ребром куба C1C (точка N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения: FN и DN (рис. 3).
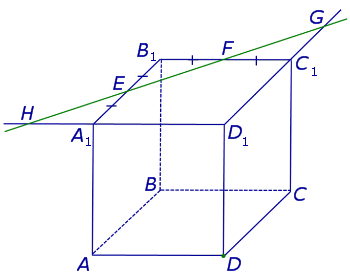
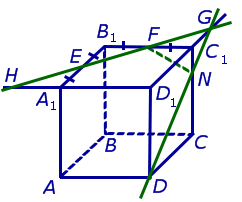
Теперь, действуя аналогичным образом, проводим прямую HD, обозначаем точку перечения этой прямой с ребром AA1 буквой M и проводим линии сечения ME и MD в плоскостях граней AA1B1B и AA1D1D (рис. 4).
В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник DMEFN.
Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.
Задача. Найти площадь сечения DMEFN, если ребро куба равно 6.
Видео:Построение натуральной величины треугольника методом вращенияСкачать

Перпендикулярные сечения призмы
Определение 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.
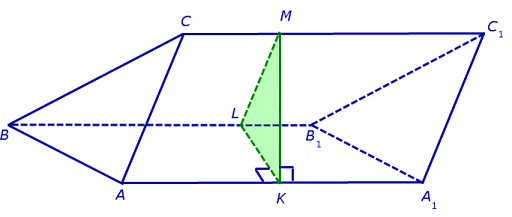
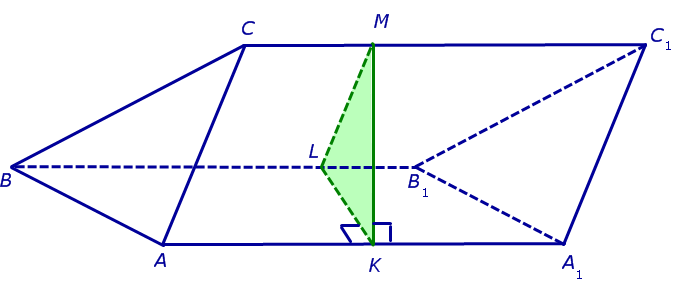
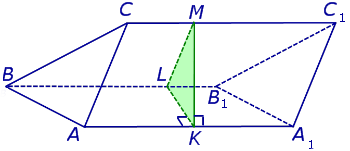
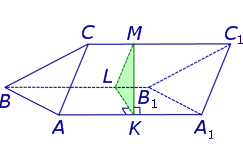
На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник KLM. Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.
Замечание 1. Все перпендикулярные сечения призмы равны между собой.
Замечание 2. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
Замечание 3. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
Видео:Задача, которую боятсяСкачать

Математика
68. В п. 63 мы научились строить прямой угол. Так как две прямые, составляющие прямые углы, называются перпендикулярными друг другу (п. 60), то построение п. 63 можно выразить словами иначе: мы можем построить прямую, перпендикулярную к данной.
Мы теперь должны эту общую задачу разобрать подробнее и прежде всего разделим ее на две отдельных задачи:
1) Дана прямая и точка на ней, построить чрез данную точку перпендикуляр к данной прямой. (Можно ли и сколько?).
2) Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой. (Можно ил и сколько?).
В скобках указаны те вопросы, которые должны быть выяснены при выполнении построений.
69. 1-я задача . Дана прямая и точка на ней; построить чрез данную точку перпендикуляр к данной прямой.
Здесь остается повторить то построение, какое было дано в п. 63.
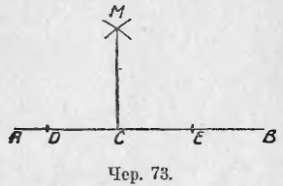
Пусть дана прямая AB и точка C на ней (чер. 73), построить чрез C перпендикуляр к AB.
От точки C откладываем по AB в разные стороны два произвольных, но равных отрезка CD = CE и затем, принимая последовательно точки D и E за центры, строим две окружности (или две дуги, достаточные для нахождения одной точки пересечения окружностей) одинаковыми радиусами, большими, чем отрезок CD. Точку пересечения M этих окружностей соединяем с C, тогда MC и есть искомый перпендикуляр, так как MC есть половина диагонали ромба, 3 вершины которого суть D, E и M.
Слово «перпендикуляр» пишут для сокращения знаком ⊥; мы построили
(CM перпендикуляр к AB).
Итак, выполнив это построение, мы можем признать, что чрез всякую точку, данную на прямой, можно построить к ней перпендикуляр (говорят иногда: восставить перпендикуляр к данной прямой). Остается еще вопрос: сколько?
Если луч CM повернуть около точки C в ту или другую сторону, то новые углы, составляемые этим лучом с прямою AB, уже не будут прямыми; поэтому заключаем, что возможно построить чрез точку прямой линии к этой прямой лишь один перпендикуляр .
70. 2-я задача . Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой.
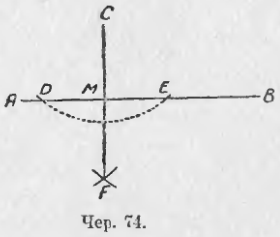
Пусть дана прямая AB и точка C вне ее (чер. 74); требуется чрез C построить перпендикуляр к AB.
Задача сводится к построению такого ромба, чтобы его одна вершина расположилась в точке C и одна его диагональ шла по прямой AB. Для построения такого ромба опишем, принимая C за центр, окружность (или дугу), выбрав ее радиус столь большим, чтобы эта окружность пересекалась с прямою AB; пусть она пересечет прямую AB в точках D и E. Тогда будут найдены еще две вершины ромба. Затем, принимая последовательно за центры точки D и E, построим два круга (или две дуги) тем же самым радиусом и найдем точку их пересечения, расположенную по другую сторону от прямой AB сравнительно с точкою C, пусть эта точка есть F. Тогда все 4 вершины ромба найдены; остается построить его диагональ CF, она, как мы знаем, и будет перпендикулярна к AB, т. е. CF ⊥ AB или CM ⊥ AB.
Стороны ромба DC, CE, EF и FD нет надобности строить.
Выполнив указанное построение, мы должны признать, что из всякой точки, данной вне прямой, мы можем построить перпендикуляр к данной прямой (говорят иногда: опустить перпендикуляр на данную прямую). Остается еще вопрос: сколько?
Для решения этого вопроса допустим, что чрез точку C (чер. 75) построено: 1) CD ⊥ AB и 2) CE ⊥ AB. Тогда ∠CDB или ∠1 и ∠CEB или ∠2 оба должны быть прямыми и, следов., равны между собою. Но ∠CEB есть внешний угол для ∆CDE, а мы знаем (п. 49), что внешний угол треугольника должен быть больше внутреннего с ним несмежного. Это противоречие показывает, что наше допущение не верно, т. е. Нельзя построить чрез точку C двух перпендикуляров к прямой AB. Итак:
Чрез точку, данную вне прямой, можно построить только один перпендикуляр к этой прямой .
Замечание . Если, как мы получили в этом п., CF ⊥ AB (чер. 74), то, очевидно, и AB ⊥ CF.
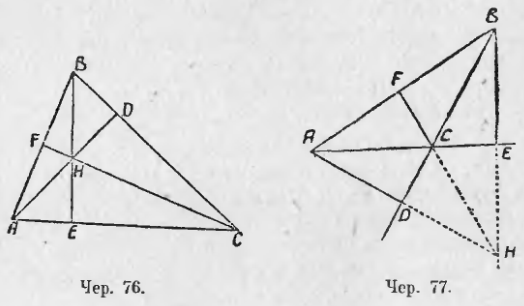
71. Построим какой-либо ∆ABC (чер. 76) и из каждой его вершины опустим перпендикуляр на противоположную сторону (здесь под именем сторона треугольника надо понимать бесконечную прямую). Каждый из этих перпендикуляров называется высотою треугольника. Следовательно, наша задача может быть выражена так: построить высоты треугольника. Если мы выполним построение перпендикуляров с возможною тщательностью, то в результате увидим, что по-видимому, все три высоты пересекаются в одной точке H, впоследствии мы выясним, что это свойство высот обязательно для всякого треугольника.
При построении высот может быть три случая: 1) все три высоты идут внутри треугольника (чер. 76); 2) две высоты BE и AD располагаются вне треугольника и общая точка H пересечения всех трех высот лежит вне треугольника (чер. 77) и 3) две высоты сливаются со сторонами треугольника (чер. 78), где BA ⊥ AC и CA ⊥ AB.
72. Для разбора вышеописанных трех случаев расположения высот условимся в обозначениях и названиях.
Прямой угол обозначают буквою d; тогда выпрямленный угол равен 2d, так как прямой угол есть половина выпрямленного угла. Если какой-либо угол больше прямого угла, то он называется тупым углом, а угол, меньший прямого угла, называется острым . Если ∠BAC (чер. 79) прямой, т. е., если ∠BAC = d, то ∠DAC > d и, следов., тупой, а ∠EAC сумма внутренних углов треугольника = 2d (или двум прямым углам ).
Ясно, что 3-й случай расположения высот в треугольнике, когда две его высоты сливаются со сторонами (чер. 78), имеет место, если ∠BAC треугольника прямой (∠BAC = d); такой треугольник с прямым углом называется прямоугольным . Так как сумма всех углов треугольника = 2d, а в этом случае ∠A прямой, или = d, то два другие угла (∠B и ∠C) в сумме составляют тоже прямой угол, а следовательно каждый из них в отдельности меньше прямого, или, другими словами, каждый из них острый угол.
Нетрудно теперь различать и два остальных случая: случай, данный на чер. 76, имеет место тогда, когда все 3 угла в треугольнике острые, а случай, данный на чер. 77, имеет место тогда, когда один из внутренних углов (на чер. 77 ∠BCA) тупой.
Ясно также, что если в треугольнике один угол тупой (или > d), то сумма двух других углов должна быть 1-й признак. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то эти прямоугольные треугольники равны.
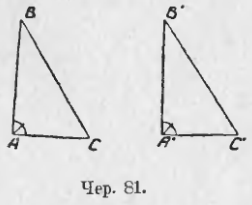
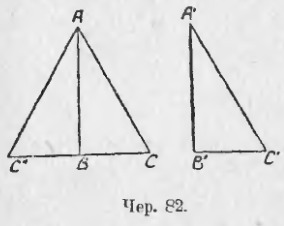
В самом деле это тот же самый признак, знакомый нам: если 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то треугольники равны. Теперь про углы не говорится потому, что между катетами расположены прямые углы, а они всегда равны (на чер. 81). ∠A = ∠A’, как прямые, и достаточно для равенства ∆ABC и ∆A’B’C’ знать, что AB = A’B’ и AC = A’C’).
2-й признак. Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то эти прямоугольные треугольники равны.
Это опять-таки знакомый нам признак: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого треугольника, то эти треугольники равны. Теперь про равенство углов, прилегающих к равным катетам у другого конца каждого, не говорится, так как эти углы прямые, а они всегда равны (на чер. 81, где ∠A и ∠A’ прямые, достаточно для равенства треугольников знать, что AB = A’B’ и ∠B = ∠B’).
Можно вместо прилежащих углов к катетам взять углы, противолежащие этим катетам: если ∠C = ∠C’, то и ∠B = ∠B’, так как ∠B + ∠C = d и ∠B’ + ∠C’ = d.
Признак равенства треугольников по трем равным сторонам здесь нет нужды применять: мы уже знаем, что для равенства прямоугольных треугольников достаточно знать равенство двух сторон, а именно двух катетов (1-й признак).
3-й признак. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого, то эти прямоугольные треугольники равны.
Этот признак является следствием общего признака: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого, то эти треугольники равны. В самом деле, пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 81), у которых BC = B’C’ и ∠С = ∠С’. Так как мы знаем, что ∠B + ∠C = d (сумма всех трех внутренних углов ∆ABC = 2d, но ∠A = d, следов., ∠B + ∠C = d) и ∠B’ + ∠C’ = d (ибо ∠A’ = d), а нам известно, что ∠C = ∠C’, то отсюда приходим к заключению, что ∠B = ∠B’ и тогда сторона BC и два прилегающих к ней угла ∠C и ∠B одного треугольника равны соответственно стороне B’C’ и двум прилегающим к ней углам другого ∠C’ и ∠B’, а мы знаем, что в этом случае ∆ABC = ∆A’B’C’.
4-й признак. Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого, то такие прямоугольные треугольники равны.
Этот признак удобнее всего выяснить следующим образом. Пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 82), причем ∠B = d и ∠B’ = d, у которых AC = A’C’ и AB = A’B’. Приложим ∆A’B’C’ и ∆ABC так, чтобы у них совпали равные катеты, т. е. A’B’ совпал бы с AB, и сами треугольники расположились бы по разные стороны от прямой AB, для этого иногда (напр., в случае, данном на чертеже) придется ∆A’B’C’ перевернуть другою стороною. Тогда сторона B’C’ должна пойти по такому направлению BC», чтобы ∠ABC» оказался прямым (ибо ∠B’ = d), а, следов., ∠CBC» оказался бы выпрямленным, т. е. Направление BC» должно быть продолжением стороны CB. Если точка C’ попадет в точку C», то, построив сторону AC», получим ∆ABC», равный ∆A’B’C’. Так как CBC» есть прямая линия, то получим еще ∆ACC», у которого сторона AC = AC», потому что AC» есть гипотенуза A’C’ треугольника A’B’C’, помещенного в положение ABC». Следовательно, ∆ACC» равнобедренный, а в таком случае углы при его основании равны, т. е. ∠C = ∠C», или ∠C = ∠C’. Оказалось, что у ∆ABC и ∠A’B’C’ имеется еще по равному острому углу, а в таком случае, на основании предыдущего признака, мы можем заключить, что ∆ABC = ∆A’B’C’.
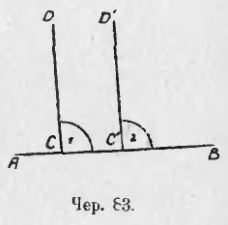
75. Пусть построено: 1) CD ⊥ AB и 2) C’D’ ⊥ AB (чер. 83); тогда, напр., ∠1 = ∠2, так как оба они прямые. Но эти углы суть соответственные при прямых CD и C’D’, пересеченных секущею AB, – следов., CD || C’D’.
Наоборот, пусть построено: 1) CD || C’D’ и 2) AB ⊥ CD (чер. 83); тогда AB должна пересечь и прямую C’D’ (п. 32, 1), напр. в точке C’. Легко увидим, что ∠2 = ∠1, так как эти углы соответственные при параллельных CD и C’D’ и секущей AB, но ∠1 = d, так как AB ⊥ CD, – следов., и ∠2 = d, т. е. AB ⊥ C’D’.
Поэтому имеем два заключения:
1) Два перпендикуляра к прямой параллельны.
2) Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.
76. Упражнения.
- Построить прямоугольный ∆ по катетам.
- Построить прямоугольный ∆ по катету и одному из острых углов.
- Построить прямоугольный ∆ по гипотенузе и острому углу.
- Построить прямоугольный ∆ по гипотенузе и катету.
- Построить высоты параллелограмма. Указать среди них равные.
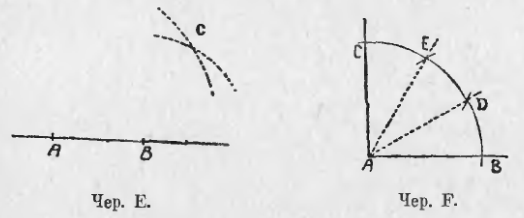
- Задачу «построить перпендикуляр к данной прямой чрез данную вне ее точку» можно решить следующим построением: на данной прямой берем 2 произвольных точки A и B (чер. E) и, принимая их последовательно за центры, построим два круга радиусами AC и BC, где C данная точка. Окончить это построение и выяснить его справедливость.
- Разделить прямой угол на 3 равных части.
Третью часть прямого угла легко построить: каждый внутренний угол равностороннего треугольника = 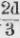
🎬 Видео
Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

ЗАДАНИЕ 1 ЕГЭ (ПРОФИЛЬ). РЕШЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.Скачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Перпендикулярные прямыеСкачать

№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать
Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Как строить сечения параллелепипедаСкачать