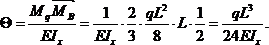Недостатком метода Мора является необходимость получать значения внутренних силовых факторов, входящих в подинтегральные выражения формул (2.18) и (2.19), в общем виде, как функций от z, что становится достаточно трудоемким уже при двух – трех участках разбиения в балках и особенно – в рамах.
Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр. Такая замена возможна в тех случаях, когда хотя бы одна из перемножаемых эпюр является прямолинейной. Этому условию соответствуют все системы, состоящие из прямолинейных стержней. Действительно, в таких системах эпюра, построенная от обобщенной единичной силы, всегда будет прямолинейной.
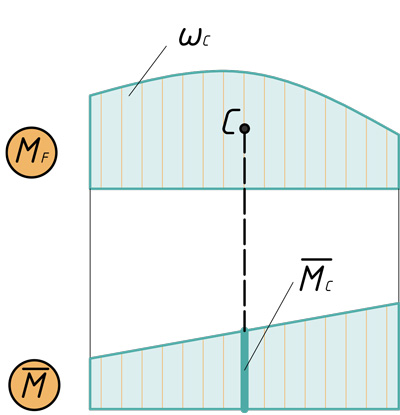
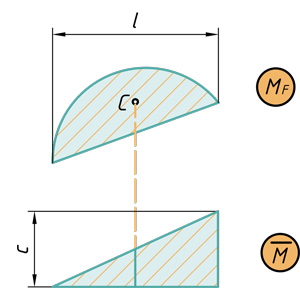
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина и заключается в следующем: чтобы перемножить две эпюры, из которых хотя бы одна является прямолинейной, нужно площадь одной эпюры (если есть криволинейная эпюра, то обязательно ее площадь) умножить на ординату другой эпюры, расположенную под центром тяжести первой.
Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (Mn) является грузовой и имеет криволинейное очертание, а вторая 
Из рис.28 следует, что 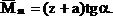
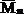
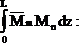

где 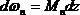
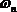
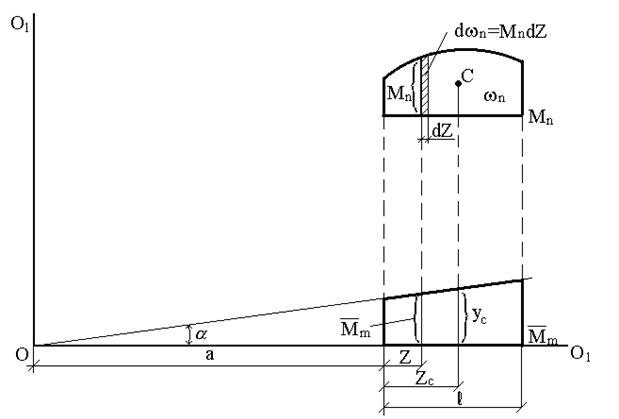
Интеграл 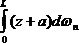
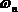
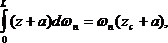
где zc – абсцисса центра тяжести площади 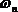
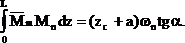
Учитывая, что 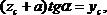
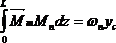
Выражение (2.20) определяет результат перемножения двух эпюр, а не перемещения. Чтобы получить перемещение, этот результат нужно разделить на жесткость, соответствующую внутренним силовым факторам, стоящим под знаком интеграла.
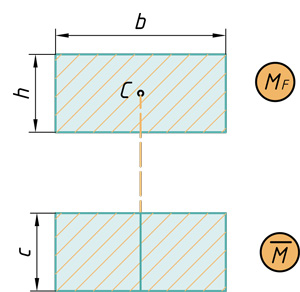
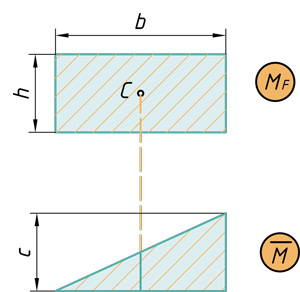
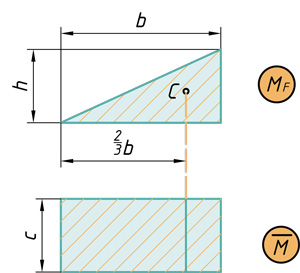
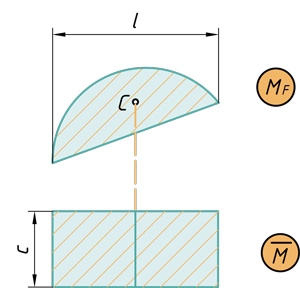
- Основные варианты перемножения эпюр
- Перемножение эпюр треугольник на треугольник
- Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение эпюр по Верещагину
- Прямоугольник на прямоугольник
- Прямоугольник на треугольник
- Треугольник на прямоугольник
- Сегмент на прямоугольник
- Сегмент на треугольник
- Частные случаи расслоения эпюр на простые фигуры
- Прямоугольник и треугольник
- Два треугольника
- Два треугольника и сегмент
- Треугольник, прямоугольник и сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр моментов
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- 🌟 Видео
Видео:Умножение эпюр. Парабола и треугольникСкачать

Основные варианты перемножения эпюр
Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.
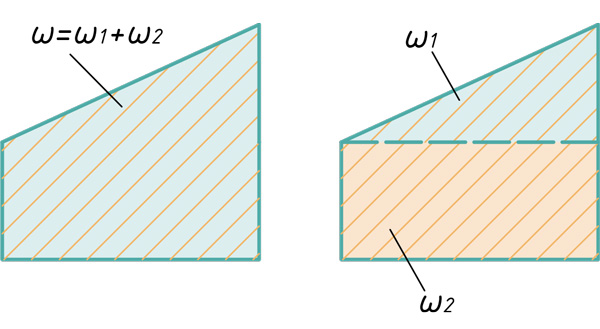
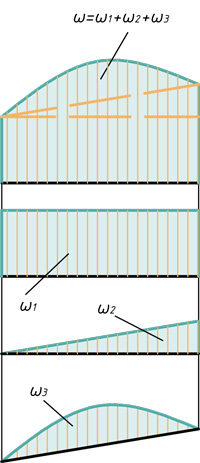
Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.
Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):
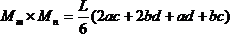
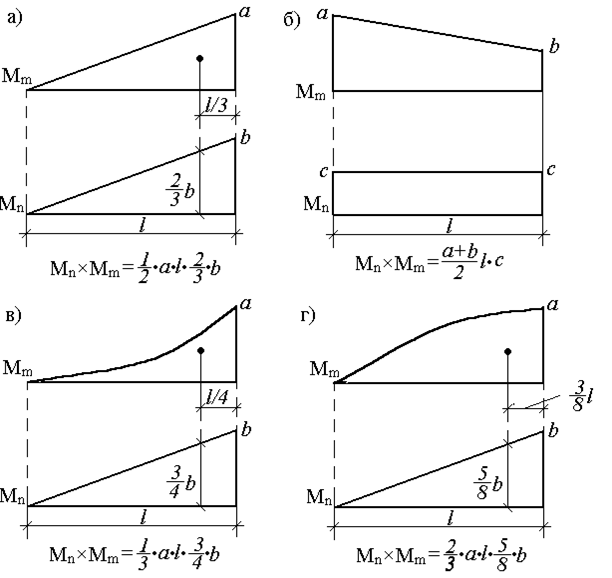
Рис. 29
По формуле (2.21) можно перемножить и эпюры, имеющих вид «перекрученных» трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.
Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:
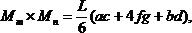
но значение f при этом определяется по-разному (рис. 30, в, г).
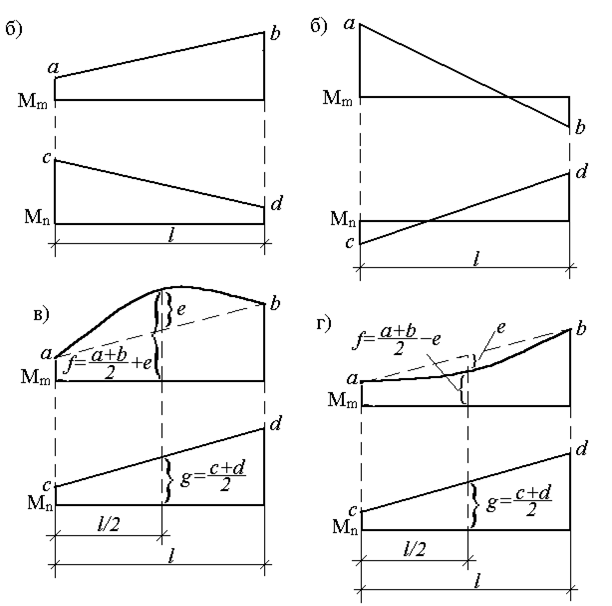
Рис. 30
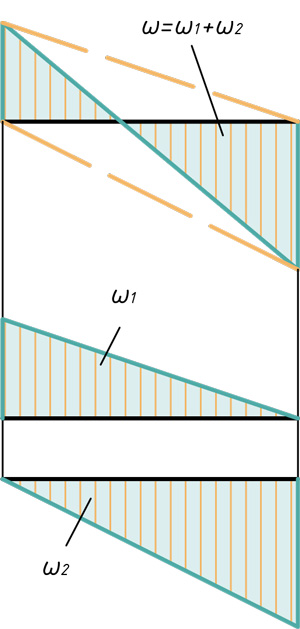
Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.
Рассмотрим использование правила Верещагина на конкретных примерах.
Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.
Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра Mq (рис.31,б), и два единичных состояния — при действии силы 
Прогиб балки в середине пролета:
Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры 
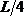
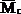
А при вычислении угла поворота сечения в точке В можно площадь эпюры Mq умножить на расположенную под ее центром тяжести ординату эпюры 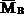
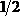
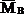
Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).
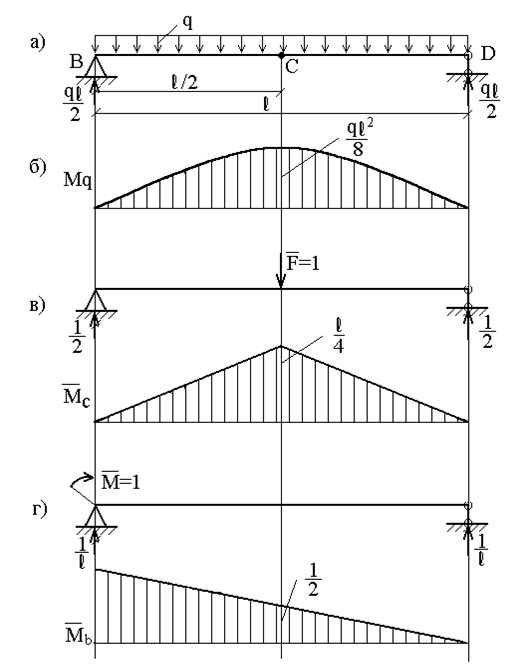
Рис. 31
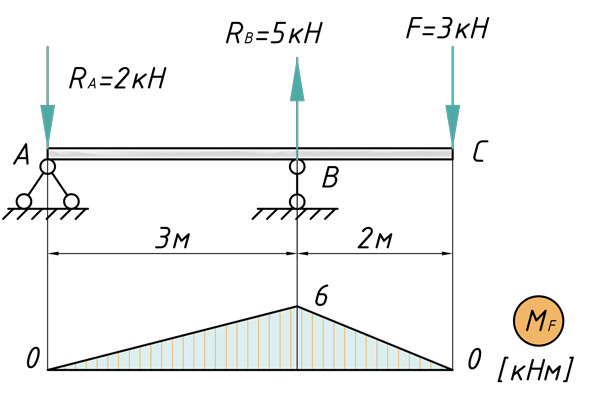
Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).
Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов MF, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу 
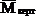
Горизонтальное перемещение точки А:
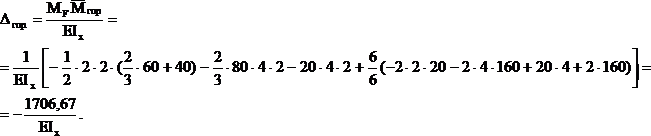
При вычислении 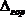
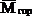
Знак » — «, полученный при вычислении 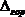
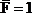
Вертикальное перемещение точки А:
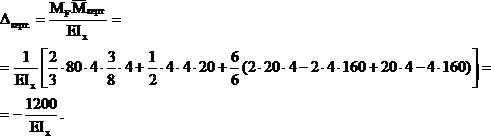
Здесь знак » — » означает, что точка А перемещается вниз, а не вверх.
Отметим, что единичные эпюры моментов, построенные от силы 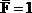
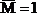
Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).
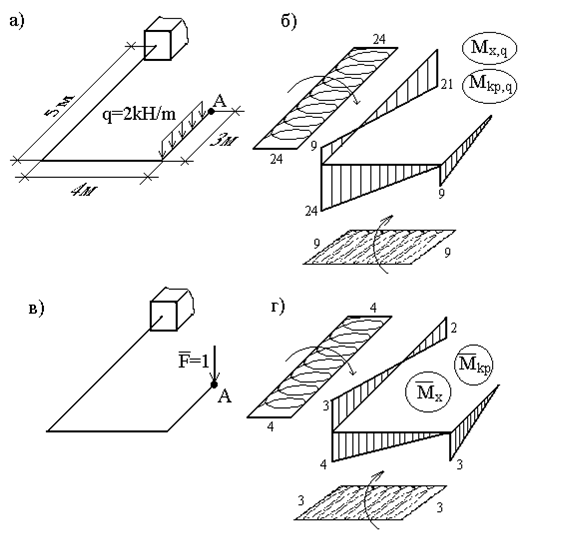
Рис.23
Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Qy, изгибающий момент Mx и крутящий момент Mкр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.
Для решения задачи построим эпюры изгибающих моментов Mx,q и крутящих моментов Мкр,q от внешней нагрузки (рис.33,б), а затем в точке А приложим силу 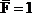
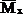
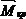
Вертикальное перемещение точки А:
При перемножении эпюр крутящих моментов произведение берется со знаком «+», если стрелки, указывающие направление кручения, сонаправленны, и со знаком » — » – в противном случае.
Видео:Правило Верещагина. Умножение эпюрСкачать

Перемножение эпюр треугольник на треугольник
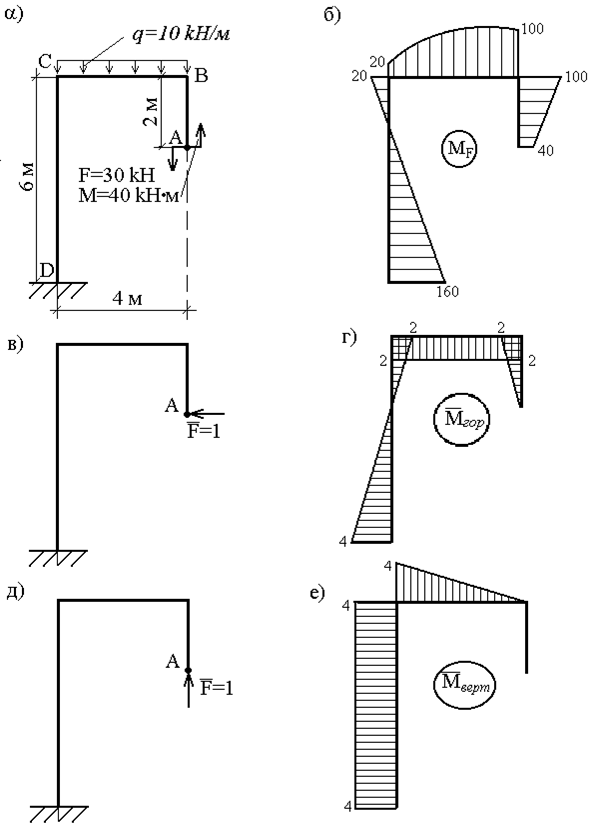
Произведение двух эпюр равно площади первой эпюры, умноженной на значение на второй эпюре напротив центра тяжести первой
$$int f(z) cdot y(z) dz =Omega cdot y_c $$
В том случае, если площадь или центр тяжести на первой эпюре посчитать сложно, ее обычно разбивают на более простые фигуры.
В нашем случае имеем:
— прямоугольник 6×12, площадь 72, центр тяжести посредине, значение напротив центра тяжести 13;
— треугольник 6×30, площадь 90, центр тяжести на 2/3 длины, значение напротив центра тяжести 3.67;
— парабола 6×54, площадь 216 (высота параболы считается по формуле qL^2/8, и не важно она горизонтально расположена или под углом, а площадь = 2/3 ширины на высоту), центр тяжести посредине, значение напротив центра тяжести 13;
$$int f(z) = -72cdot13+90cdot3.67+216cdot13=2202$$знак «-» ставим, если первая эпюра и значение на второй расположены по разные стороны стержня.
Видео:Перемножение эпюр по Верещагину. СопроматСкачать

Перемножение эпюр по правилу, методу или способу Мора-Верещагина: формула, таблица, примеры и задачи
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем, это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Видео:15. Правило Верещагина ( практический курс по сопромату )Скачать

Верещагин и его метод, правило или способ
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть любой. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем не важно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
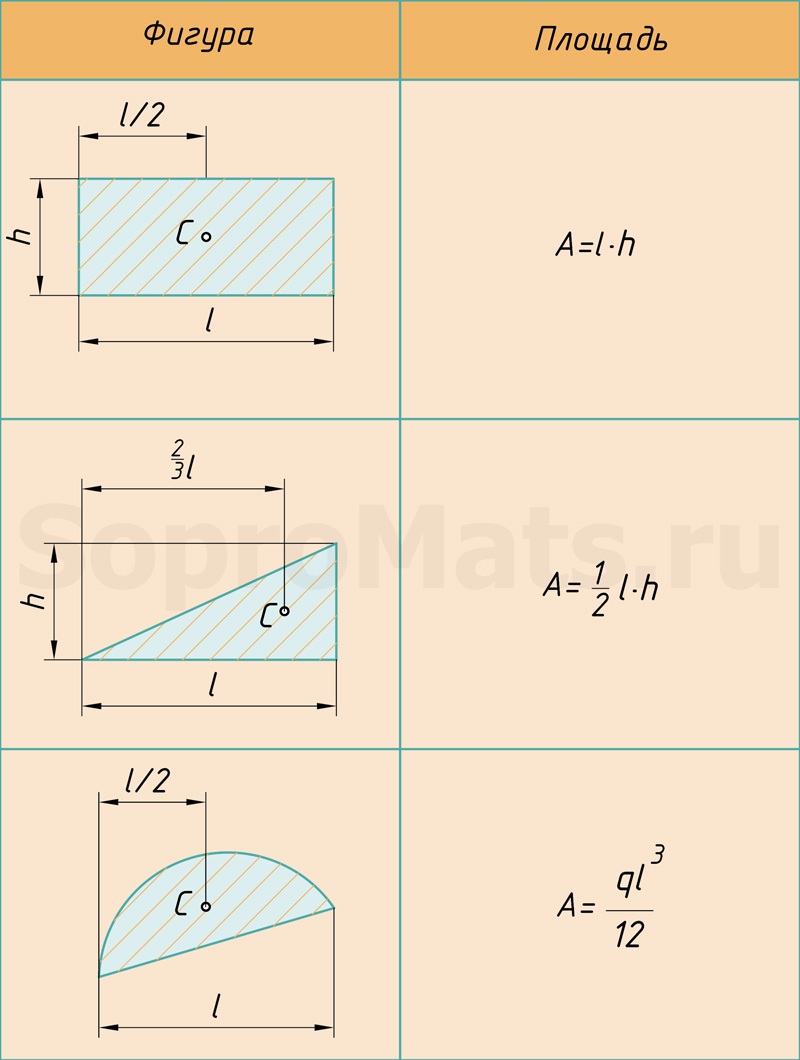
При использовании метода Верещагина, берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любую эпюру можно расслоить всего на три фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Видео:Перемножение эпюр, правило верещагинаСкачать

Перемножение эпюр по Верещагину
В этом блоке статьи покажу частные случаи перемножения эпюр по Верещагину.
Прямоугольник на прямоугольник
Прямоугольник на треугольник
Треугольник на прямоугольник
Сегмент на прямоугольник
Сегмент на треугольник
Видео:Метод Верещагина. Перемножение эпюр по правилу Верещагина. Определение прогиба балки, сопроматСкачать

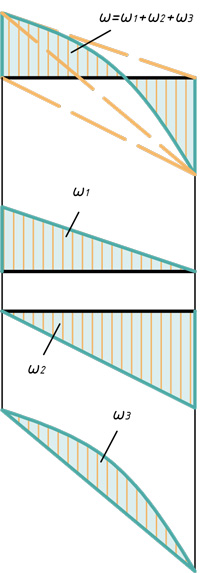
Частные случаи расслоения эпюр на простые фигуры
В этом блоке статьи покажу частные случаи расслоения эпюр на простые фигуры, для возможности их перемножения по Верещагину.
Прямоугольник и треугольник
Два треугольника
Два треугольника и сегмент
Треугольник, прямоугольник и сегмент
Видео:Перемножение эпюр по Симпсону. СопроматСкачать

Пример определения перемещений: прогибов и углов поворотов по Верещагину
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь, рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр моментов
Теперь для каждого искомого перемещений необходимо приложить единичную нагрузку (безразмерную величину равную единице) и построить единичные эпюры:
- Для прогибов, прикладываются единичные силы.
- Для углов поворотов, прикладываются единичные моменты.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой силы. Тоже самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ _=frac < E_ > (frac cdot 6cdot 3cdot frac cdot 2+frac cdot 6cdot 2cdot frac cdot 2)=frac < 20кН^ >< E_ > ]
Представим, что рассчитываемая балки имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
🌟 Видео
Методы Симпсона и Верещагина. Перемножение эпюр. СтроймехСкачать

Формула Мора. Перемножение эпюр по способу ВерещагинаСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать
Задание: ЭпюрСкачать

Сопротивление материалов. G-03 (способ Верещагина, расслоение эпюр, основные фигуры для расслоения).Скачать

"Перемножение" эпюр для вычисления интеграла Мора "комбинированным" способомСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать
Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

"Перемножение" эпюр для вычисления интеграла Мора с использованием формулы Симпсона (продолжение)Скачать

Расслоение эпюр (временное видео)Скачать

16. Формула Симпсона ( практический курс по сопромату )Скачать