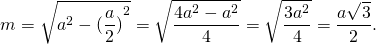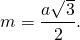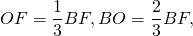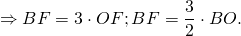Отношение медианы в равностороннем треугольнике

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S₁ = S₂.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Видео:Задание 9 ОГЭ от ФИПИСкачать

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

• BG = 8 см (самая большая сторона, является гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Медиана равностороннего треугольника

Какими свойствами обладает медиана равностороннего треугольника? Как выразить длину медианы через сторону треугольника? Через радиус вписанной и описанной окружностей?

(свойство медианы равностороннего треугольника)

В равностороннем треугольнике медиана, проведённая к любой стороне, является также его биссектрисой и высотой.

Пусть в треугольнике ABC AB=BC=AC.

Проведём медиану BF.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

По свойству медианы равнобедренного треугольника, BF является также его биссектрисой и высотой.

Аналогично, так как AB=AC, треугольник ABC — равнобедренный с основанием BC, AK — его медиана, биссектриса и высота;

так как AC=BC, треугольник ABC — равнобедренный с основанием AB, CD — его медиана, биссектриса и высота.

Что и требовалось доказать .

(свойство медиан равностороннего треугольника)

Все три медианы равностороннего треугольника равны между собой.

Пусть в треугольнике ABC AB=BC=AC,

AK, BF, CD — его медианы.

Следовательно, треугольники ABK, BCF и CAK равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон:

Что и требовалось доказать .

Из 1 и 2 теоремы следует, что все медианы, биссектрисы и высоты равностороннего треугольника равны между собой.

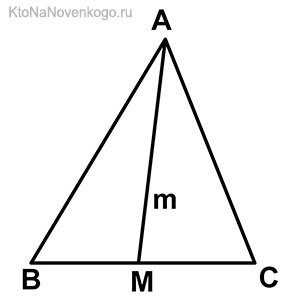
1) Выразим длину медианы равностороннего треугольника через его сторону.

Так как медиана равностороннего треугольника является также его высотой, треугольник ABF- прямоугольный.

Обозначим AB=a, BF=m, тогда AF=a/2.

Таким образом, формула медианы равностороннего треугольника по его стороне:

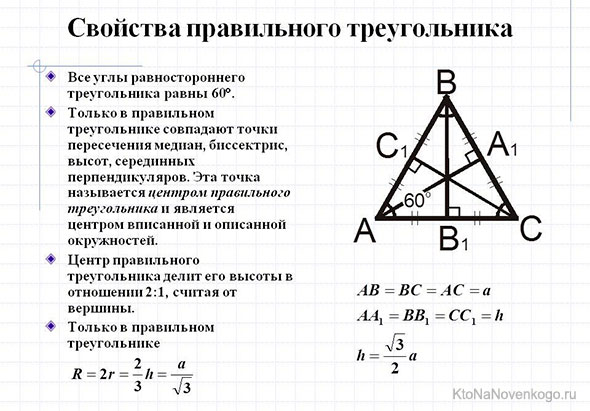
2) Выразим медиану равностороннего треугольника через радиусы вписанной и описанной окружностей.

Центр правильного треугольника является центром его вписанной и описанной окружностей.

Так как центр вписанной окружности лежит в точке пересечения биссектрис треугольника, а медианы равностороннего треугольника являются также его биссектрисами, в равностороннем треугольнике ABC OF — радиус вписанной, BO — радиус описанной окружностей:

Так как медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то BO:OF=2:1. Таким образом,

Отсюда медиана равностороннего треугольника через радиус вписанной окружности равна

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Медиана — это золотое сечение треугольника

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком понятии в математике, как МЕДИАНА.

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

Видео:8. Медиана треугольника и её свойства.Скачать

Медиана — это.

Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

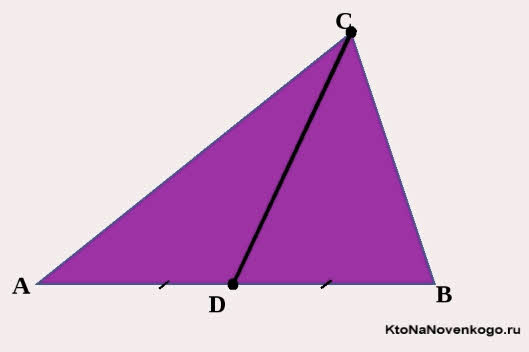
Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.

Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:

Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.

Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.

И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!

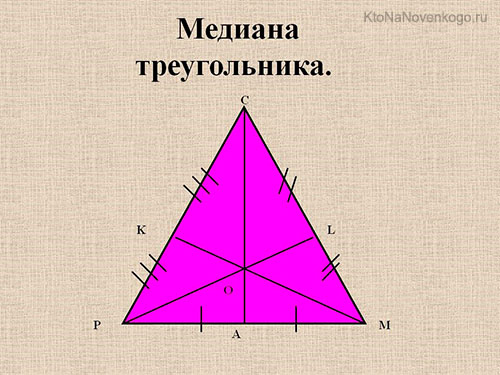
И выглядят они вот так.

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Видео:ОГЭ 16🔴Скачать

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

1. Отрезок СО вдвое больше, чем отрезок АО;
2. Отрезок РО вдвое больше, чем отрезок LO;
3. Отрезок МО вдвое больше, чем КО.

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

Видео:Теорема о свойстве медианы равнобедренного треугольникаСкачать

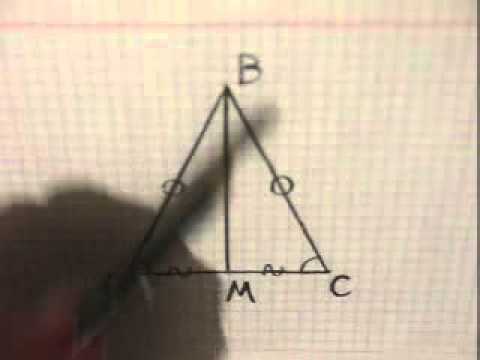
Медиана равностороннего треугольника

Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.

И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

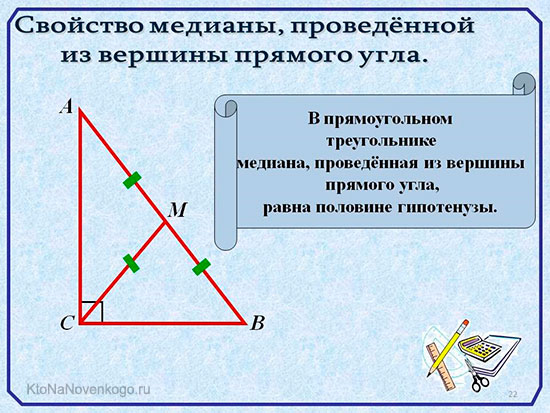
Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

Видео:Формулы равностороннего треугольника #shortsСкачать

Вместо заключения

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?

💡 Видео

Равнобедренный треугольник. 7 класс.Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Все свойства медианы в одной задаче.Скачать

Свойства равнобедренного треугольника. 7 класс.Скачать

9 класс. Геометрия. Соотношения в равностороннем треугольнике.Скачать

Задача найти сторону равностороннего треугольника по медианеСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Равносторонний треугольник Радиусы описанной и вписанной окружностей Часть 2Скачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать