Тетраэдр — это частный случай правильной треугольной пирамиды.
Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
Медиана тетраэдра — это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
Бимедиана тетраэдра — это отрезок, который соединяет середины рёбер, что скрещиваются (соединяет середины сторон треугольника, который есть одной из граней тетраэдра).
Высота тетраэдра — это отрезок, который соединяет вершину и точку противоположной грани и перпендикулярен этой грани (т.е. это высота, проведенная от всякой грани, кроме того, совпадает с центром описанной окружности).
- Свойства тетраэдра.
- Типы тетраэдров.
- Формулы для определения элементов тетраэдра.
- Основание тетраэдра это равносторонний треугольник
- Определение
- Свойства правильной треугольной пирамиды:
- Формулы для правильной треугольной пирамиды
- Тетраэдр
- Тетраэдр
- Поэтому на вопрос — «что такое тетраэдр?», можно дать следующее определение: » Тетраэдр это геометрическое тело из четырех граней, каждая их которых — правильный треугольник «.
- Математические характеристики тетраэдра
- Вариант развертки
- Видео. Тетраэдр из набора «Волшебные грани»
- Видео. Вращение всех правильных многогранников
- Популярное
- 💡 Видео
Видео:Тетраэдр. 10 класс.Скачать

Свойства тетраэдра.
Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.
Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.
Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.
Видео:10 класс, 12 урок, ТетраэдрСкачать

Типы тетраэдров.
Правильный тетраэдр — это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.
Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.
Правильный тетраэдр — это один из 5-ти правильных многогранников.
Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:
— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.
— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.
— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.
— Каркасный тетраэдр — тетраэдр, который таким условиям:
- есть сфера, которая касается каждого ребра,
- суммы длин ребер, что скрещиваются равны,
- суммы двугранных углов при противоположных ребрах равны,
- окружности, которые вписаны в грани, попарно касаются,
- каждый четырехугольник, образующийся на развертке тетраэдра, — описанный,
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке.
— Соразмерный тетраэдр, бивысоты у него одинаковы.
— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.
Видео:Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать

Формулы для определения элементов тетраэдра.
Высота тетраэдра:
где h — высота тетраэдра, a — ребро тетраэдра.
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
где V — объем тетраэдра, a — ребро тетраэдра.
Основные формулы для правильного тетраэдра:
Где S — Площадь поверхности правильного тетраэдра;
h — высота, опущенная на основание;
r — радиус вписанной в тетраэдр окружности;
Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать
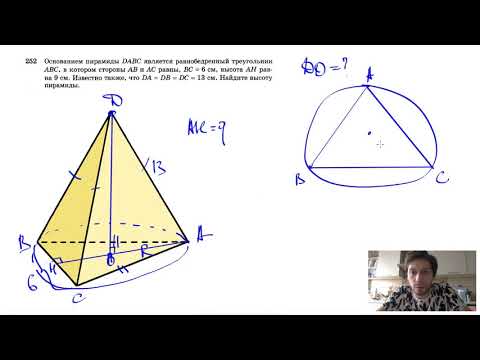
Основание тетраэдра это равносторонний треугольник
| Учебный курс | Решаем задачи по геометрии |
В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока. Видео:Формулы равностороннего треугольника #shortsСкачать  ОпределениеПравильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания. На рисунке обозначены: Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже). Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать  Свойства правильной треугольной пирамиды:
Формулы для правильной треугольной пирамидыФормула объема правильной треугольной пирамиды: V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды. Примеры решения задач: Видео:Как строить сечения тетраэдра и пирамидыСкачать  ТетраэдрЧастным случаем правильной треугольной пирамиды является тетраэдр. Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.
Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине) Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра) Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности). Тетраэдр обладает следующими свойствами:
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать  ТетраэдрДревние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» — означает грань (тетраэдр – четырехгранник). Видео:Два тетраэдраСкачать  Поэтому на вопрос — «что такое тетраэдр?», можно дать следующее определение: » Тетраэдр это геометрическое тело из четырех граней, каждая их которых — правильный треугольник «.Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел . Тетраэдр имеет следующие характеристики:
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°. Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны. Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник. Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани. Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать  Математические характеристики тетраэдраТетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы. Радиус описанной сферы тетраэдра определяется по формуле: , где a — длина стороны. Сфера может быть вписана внутрь тетраэдра. Радиус вписанной сферы тетраэдра определяется по формуле: Площадь поверхности тетраэдра Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой: Объем тетраэдра определяется по следующей формуле: Высота тетраэдра определяется по следующей формуле: Расстояние до центра основания тетраэдра определяется по формуле: Видео:Нахождение высоты тетраэдра.Скачать  Вариант разверткиТетраэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов. Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет. Заметим, что это не единственный вариант развертки. Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4: Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать  Видео. Тетраэдр из набора «Волшебные грани»Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани». Сборка многогранника из набора: Подробная сборка от Алексея Жигулева (youtube-канал PRO) Подробная сборка от Алексея Жигулева (youtube-канал PRO) вращение готового многогранника: Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать  Видео. Вращение всех правильных многогранниковПопулярноеСовершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Для Вашего удобства мы снизили стоимость доставки наборов «Волшебные грани» в разы! Основатели города Мирный, находящегося в Архангельской области разместили на флаге и гербе своего города многогранник – «Большой додекаэдр». Нечасто удается встретить многогранники за пределами учебников математики. И если такие геометрические формы как куб, призма и цилиндр встречаются повседневно, то. Если ты не любишь математику, опасайся хэллоуина! Злые силы придут за тобой в хэллоуин! Создай двух стражей, которые будут оберегать тебя от злых сил! Ну, или. Многогранник — (определение) геометрическое тело, ограниченное со всех сторон плоскими многоугольниками — гранями. 1. Вы хотели бы увидеть, как можно преобразовать развертку обычного куба? Если да, то следующий. 💡 ВидеоТетраэдр. Видеоурок 5. Геометрия 10 классСкачать  Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать  №250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать 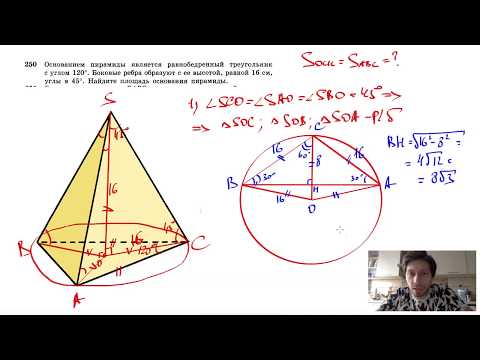 Геометрия 10 класс (Урок№7 - Тетраэдр и параллелепипед.)Скачать  Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  №251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать  Объем пирамиды. Практическая часть. 11 класс.Скачать  |
























