Объясните как построить треугольники

Задача:

Построить треугольник по двум сторонам и углу между ними с помощью циркуля и линейки (без масштабных делений).

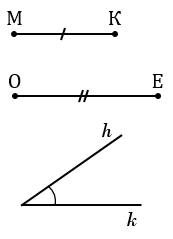
Дано: отрезки МК и ОЕ, 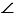hk.

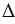
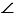
Построить АВС такой, что АВ = МК, АС = ОЕ, ВАС =hk.

Решение:

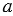
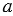
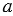
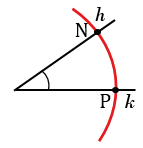
С помощью линейки проводим прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой обозначаем В.

Далее строим угол ВАF равный углу hk. Для этого строим с помощью циркуля окружность радиуса МК с центром в вершине угла hk (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла hk обозначаем N и Р.

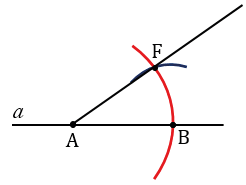
С помощью циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения данной окружности с окружностью радиуса МК с центром в точке А обозначаем F.

Далее, проводим луч АF с помощью линейки.

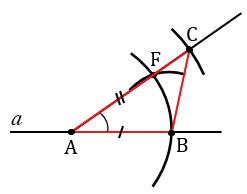
Затем, с помощью циркуля измеряем отрезок ОЕ и строим окружность радиуса ОЕ с центром в точку А (всю окружность строить необязательно, смотри, выделенное зеленым цветом). Точку пересечения данной окружности с лучом АF обозначаем С.

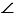
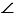
Теперь с помощью линейки соединяем точки В и С. Получаем треугольник АВС, в котором по построению АВ = МК, АС = ОЕ, ВАС =hk, следовательно, треугольник АВС — искомый.

При любых данных отрезках МК, ОЕ и данном неразвернутом угле hk искомый треугольник построить можно. Прямую 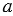и точку А на ней можно выбрать произвольно, значит, существует бесконечно много треугольников, удовлетворяющих условиям задачи, Все эти треугольники будут равны друг другу по первому признаку равенства треугольников (по двум сторонам и углу между ними), поэтому принято говорить, что данная задача имеет единственное решение.

Поделись с друзьями в социальных сетях:

Видео:Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать

Построение треугольников. Задачи на построение

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

Видео:Построение угла, равного данному. 7 класс.Скачать

Построение треугольника по двум сторонам и углу между ними

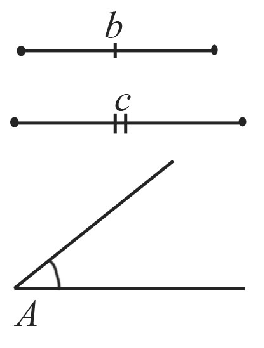
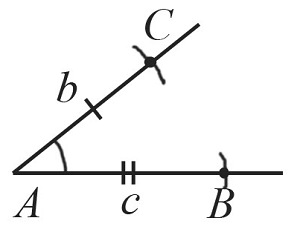
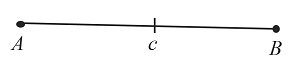
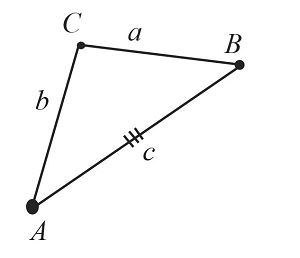
Пусть даны два отрезка $b$ и $с$ и угол $А$:

Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

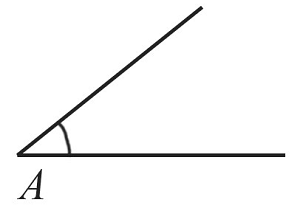
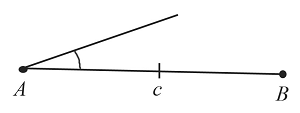
Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

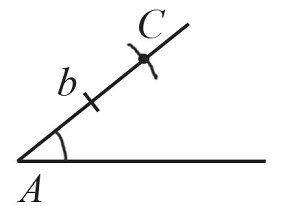
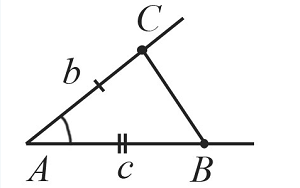
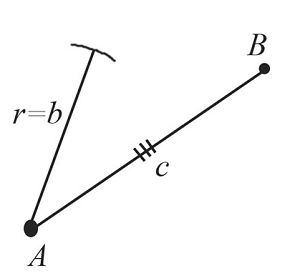
С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

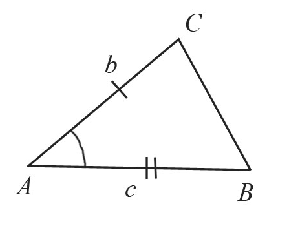
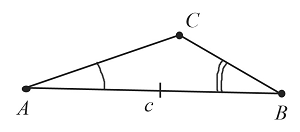
Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Видео:Построение биссектрисы углаСкачать

Построение треугольника по стороне и прилегающим к ней углам

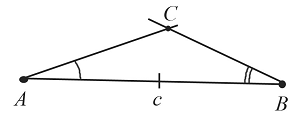
Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

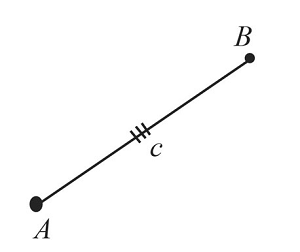
Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Построение треугольника по трем сторонам

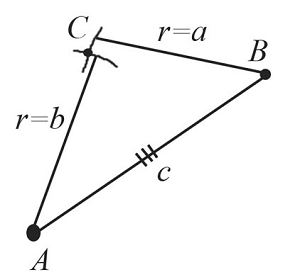
Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

Построим отрезок $АВ$, который равен заданному отрезку $c$.

Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

Видео:Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Построение треугольников с помощью циркуля и линейки

Просмотр содержимого документа
«Построение треугольников с помощью циркуля и линейки»

Построение треугольников с помощью циркуля и линейки

Какие стандартные задачи на построение Вы знаете?

• Построение угла, равного данному;

• Построение биссектрисы угла;

• Деление отрезка пополам ;

• Построение перпендикулярной прямой;

• Построение треугольника по трём сторонам.

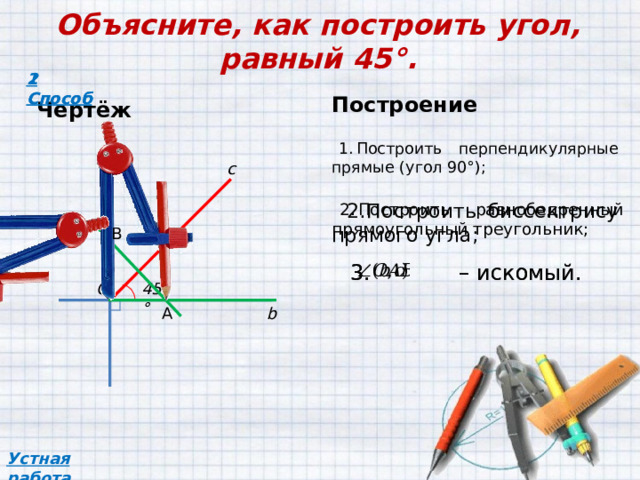
Объясните, как построить угол, равный 45°.

• Построить перпендикулярные прямые (угол 90°);

• Построить равнобедренный прямоугольный треугольник;

• Построить биссектрису прямого угла;

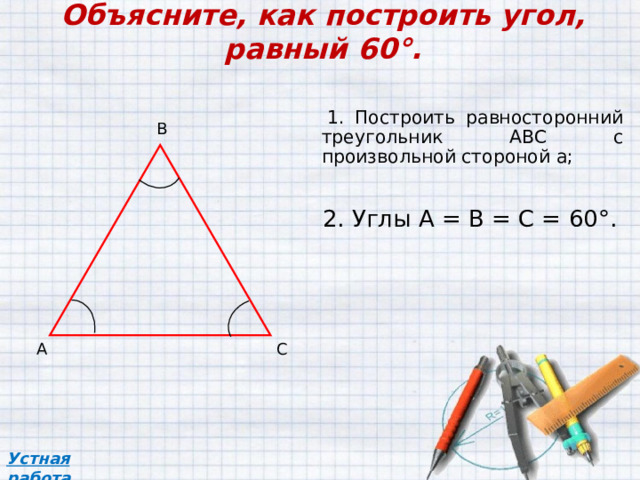
Объясните, как построить угол, равный 60°.

1. Построить равносторонний треугольник АВС с произвольной стороной a ;

2. Углы А = В = С = 60°.

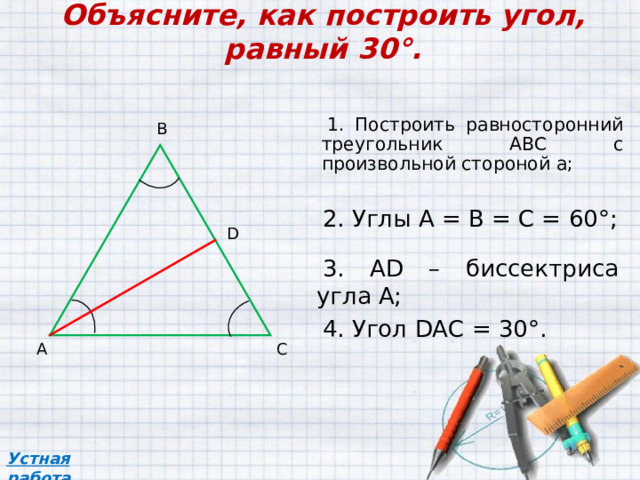
Объясните, как построить угол, равный 30°.

1. Построить равносторонний треугольник АВС с произвольной стороной a ;

2. Углы А = В = С = 60°;

3. А D – биссектриса угла А;

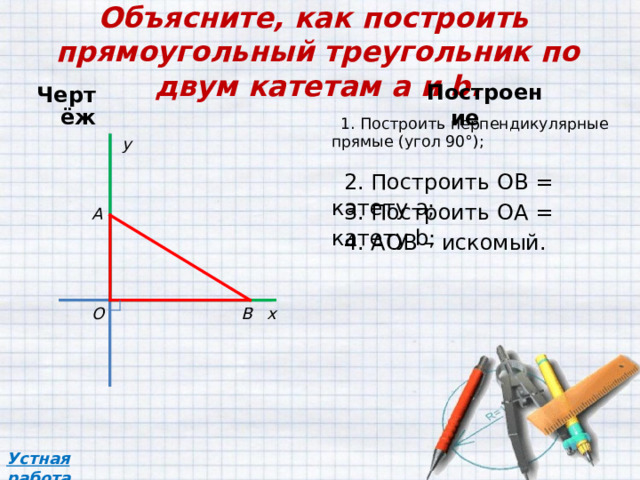
Объясните, как построить прямоугольный треугольник по двум катетам a и b .

1. Построить перпендикулярные прямые (угол 90°);

2 . Построить OB = катету а;

3. Построить O А = катету b ;

4. А OB – искомый.

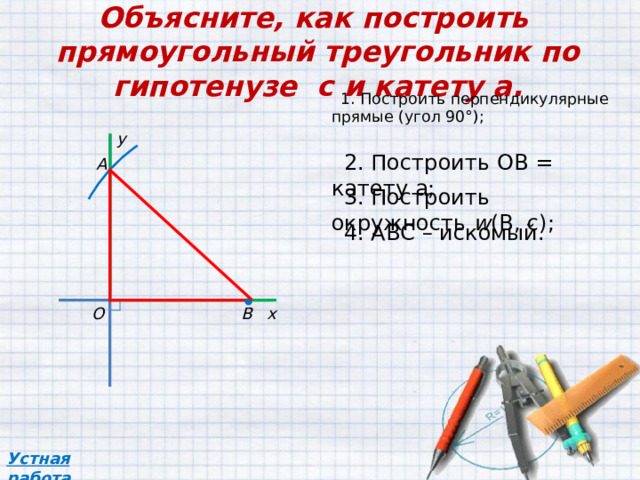
Объясните, как построить прямоугольный треугольник по гипотенузе c и катету a .

1. Построить перпендикулярные прямые (угол 90°);

2 . Построить OB = катету а;

3 . Построить окружность w (В, с);

4 . АВС – искомый.

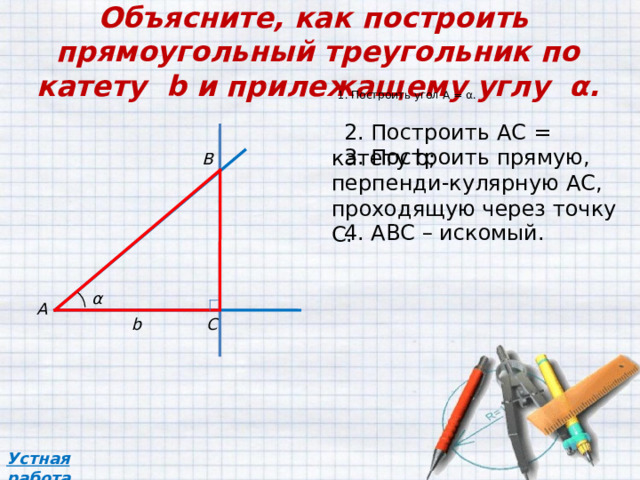
Объясните, как построить прямоугольный треугольник по катету b и прилежащему углу α.

1. Построить угол А = α .

2 . Построить АС = катету b ;

3 . Построить прямую, перпенди-кулярную АС, проходящую через точку С.

4 . АВС – искомый.

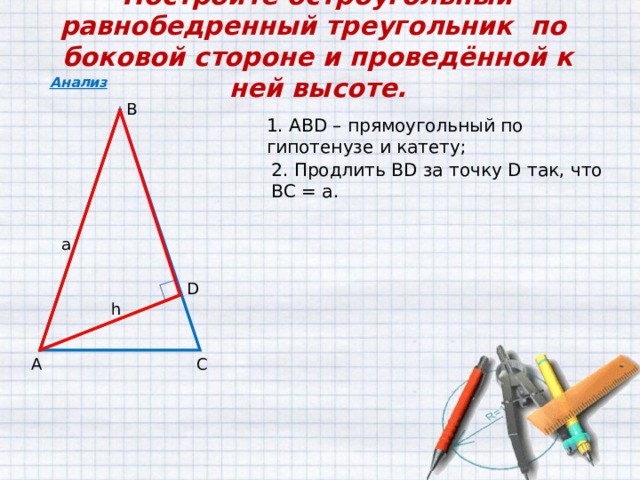
Постройте остроугольный равнобедренный треугольник по боковой стороне и проведённой к ней высоте.

1. АВ D – прямоугольный по гипотенузе и катету;

2. Продлить В D за точку D так, что ВС = а.

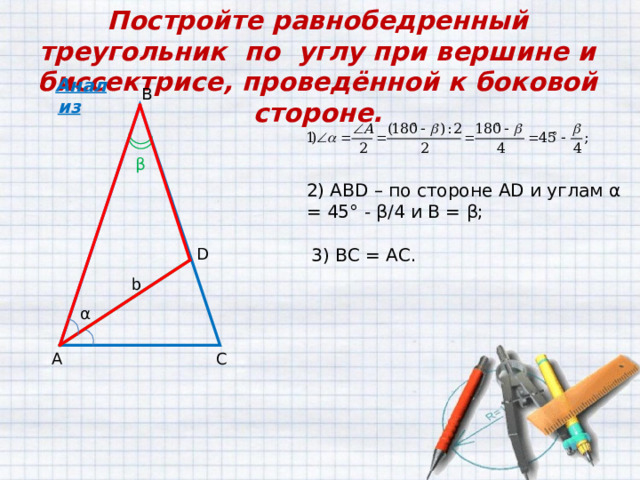
Постройте равнобедренный треугольник по углу при вершине и биссектрисе, проведённой к боковой стороне.

2 ) АВ D – по стороне AD и углам α = 45° — β /4 и B = β ;

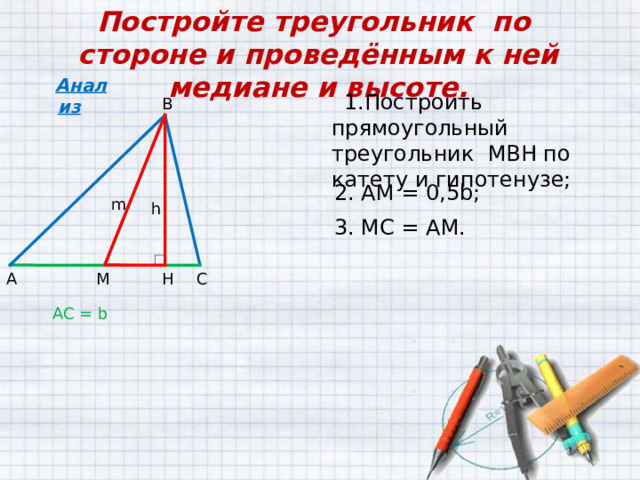
Постройте треугольник по стороне и проведённым к ней медиане и высоте.

• Построить прямоугольный треугольник МВН по катету и гипотенузе;

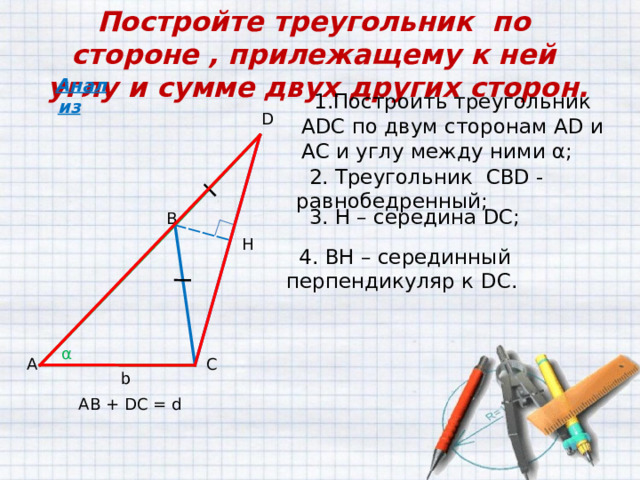
Постройте треугольник по стороне , прилежащему к ней углу и сумме двух других сторон.

• Построить треугольник ADC по двум сторонам AD и AC и углу между ними α ;

2. Треугольник CBD — равнобедренный;

3. Н – середина DC ;

4. ВН – серединный перпендикуляр к DC .

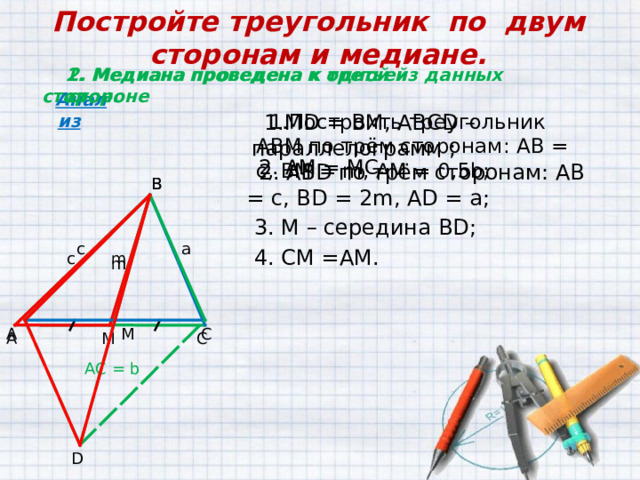
Постройте треугольник по двум сторонам и медиане.

1. Медиана проведена к одной из данных сторон.

2. Медиана проведена к третьей стороне

• М D = ВМ, ABCD – параллелограмм ;

• Построить треугольник АВМ по трём сторонам: АВ = с, ВМ = m, АМ = 0 , 5b ;

2. ABD по трём сторонам: АВ = с, В D = 2m , AD = а;

🌟 Видео

Построение треугольника по трем сторонам. 7 класс . Геометрия.Скачать

Построение угла равного данномуСкачать

Построение треугольника, равного данномуСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Построение биссектрисы углаСкачать

Треугольники. 7 класс.Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Построить угол , равный данному.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Построение биссектрисы в треугольникеСкачать

Построение биссектрисы угла. 7 класс.Скачать

Построение середины отрезкаСкачать

Математика 2 класс (Урок№33 - Угол. Виды углов: прямой, острый, тупой.)Скачать