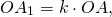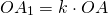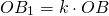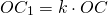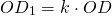Образ треугольника при гомотетии (5 видео)

Свойства, типы и примеры гомотетии

homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.

Тогда гомотетия — это соответствие между двумя геометрическими фигурами, где преобразованные точки называются гомотетическими, и они выровнены с фиксированной точкой и сегментами, параллельными друг другу..

1 гомотеция
2 свойства
3 типа
- 3.1 Прямая гомотетия
- 3.2 Обратная гомотетия
4 Композиция
5 примеров
- 5.1 Первый пример
- 5.2 Второй пример
6 Ссылки

Содержание

homotecia
свойства
Гомотетия
Применение геометрических преобразований к решению задач
ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ
📺 Видео

Видео:9 класс. Геометрия. Гомотетия.Скачать

homotecia

Гомотетия — это преобразование, которое не имеет конгруэнтного изображения, потому что из рисунка будет получена одна или несколько фигур большего или меньшего размера, чем исходная фигура; то есть гомотетия превращает многоугольник в другой подобный.

Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..

Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:

Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..

С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..

Видео:ГомотетияСкачать

свойства

Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:

— Центр гомотетии (O) — единственная двойная точка, и она превращается в себя; то есть не меняется.

— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.

— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.

— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:

— Гомотетические углы конгруэнтны; то есть они имеют одинаковую меру. Следовательно, изображение угла — это угол, имеющий одинаковую амплитуду..

С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:

— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.

— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).

— Если k = -1, гомотетия становится центральной симметрией (C); то есть вращение вокруг C будет происходить под углом 180 или .

— Если k> 1, размер преобразованного рисунка будет больше размера исходного.

— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:

Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.

Видео:Гомотетия. Коэффициент гомотетии. Центр гомотетии. Гомотетичные фигуры. Геометрия 8-9 классСкачать

Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

и соединить вершины A1, B1, C1и D1 отрезками.

При k

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Видео:Геометрия, 9 класс, Гомотетия и ее свойстваСкачать

Применение геометрических преобразований к решению задач

Видео:Геометрия. 9 класс. Гомотетия и ее свойства /26.11.2020/Скачать

ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ К РЕШЕНИЮ ЗАДАЧ

Ученики 10 класса хорошо знакомы, а ученики 9 класса уже познакомились с такими геометрическими преобразованиями плоскости как поворот вокруг некоторой точки на заданный угол, параллельный перенос, осевая и центральная симметрии. Наша задача: сделать небольшой шаг за рамки школьного учебника и изучить еще несколько замечательных преобразований плоскости. Начнем мы с гомотетии.

Определение 1. Гомотетией с центром в точке М0 и коэффициентом k называется правило, по которому каждая точка М отображается в точку М’, и при этом выполняется условие:

(1).

Две фигуры назовем гомотетичными, если одна может быть получена и другой с помощью некоторой гомотетии.

Рассмотрим примеры гомотетии с различными коэффициентами.

На первом рисунке построен образ треугольника АВС при гомотетии с коэффициентом 2, а на втором – приведен пример гомотетии с коэффициентом -2. Наблюдательный читатель сразу заметит, что на обоих чертежах изображены пары подобных треугольников. Причем в обоих случаях коэффициент подобия равен 2. Кроме того, хорошо видно, что соответствующие стороны треугольника АВС и треугольника А’В’С’ – попарно параллельны.

Сформулируем основные свойства гомотетии.

Свойство 1. При гомотетии точка отображается в точку, отрезок в отрезок, а прямая в прямую.

Свойство 2. Гомотетия сохраняет принадлежность объектов (инцидентность). Другими словами, если точка принадлежит некоторой фигуре, то ее образ будет принадлежать образу этой фигуры, и наоборот.

Свойство 3. Гомотетия сохраняет параллельность. То есть, две параллельные прямые отображаются в две параллельные прямые.

Свойство 4. Гомотетия прямую отображает в параллельную ей прямую.

Рассмотрим важное следствие их этих свойств.

Следствие 1. Гомотетия любую фигуру отображает в подобную ей, причем коэффициент подобия равен модулю коэффициента гомотетии.

Доказательство. Достаточно показать, что это утверждение выполняется для треугольников. (Используем следующий признак подобия: два треугольника подобны, если соответственные углы у них равны.)

Равенство соответственных углов вытекает из свойства 4. Действительно, соответственные стороны исходного треугольника и его образа попарно параллельны, а это приводит к равенству углов.

Осталось доказать, что коэффициент подобия равен модулю коэффициента гомотетии. Рассмотрим чертеж на рисунке 3. Из определения гомотетии следует, что

(2).

Из этого, по свойству пропорциональных отрезков, следует, что АВ параллельна А’В’, откуда вытекает, что треугольники М0АВ и М0А’В’ подобны, так как у них пропорциональны длины сторон, прилежащих к общему (или вертикальным, если k