Начертить равносторонний тупоугольный треугольник

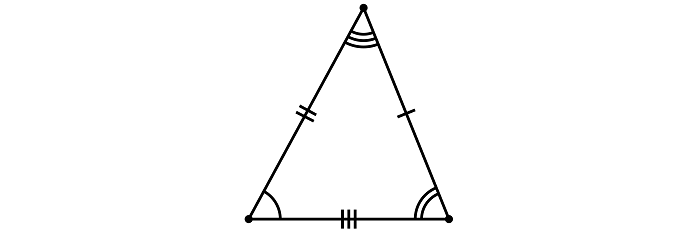
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Как построить тупоугольный треугольник

Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является тупым углом.

Видео:Геометрия - Построение правильного треугольникаСкачать

Разбираемся с понятиями

В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.

Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения площади треугольника математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.

Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Правильное начертание

Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о .

Видео:Построение равностронего треугольника.Скачать

Основные линии

Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.

Так, биссектрисы делят угол пополам, а противоположную сторону – на отрезки, которые пропорциональны прилегающим сторонам.

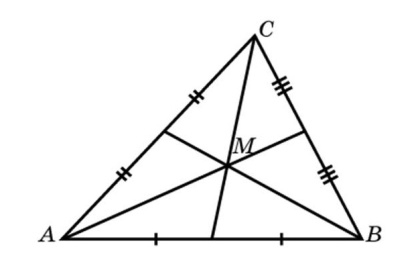
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2 : 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.

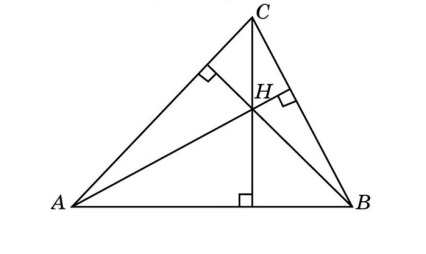
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.

Серединный перпендикуляр – это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Работа с окружностями

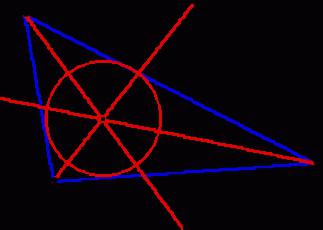
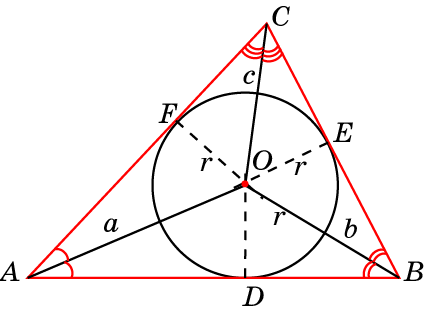
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.

Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.

Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.

Видео:КАК НАЧЕРТИТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИКСкачать

Вписанные треугольники

Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном – за его пределами.

Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R – это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о .

Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Описанные треугольники

Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.

Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.

Радиус такой окружности, вписанной в тупоугольный треугольник, равняется квадратному корню из частного (p-c) х (p-v) х (p-b) : p. При этом p – это полупериметр треугольника, c, v, b – его стороны.

Видео:Виды треугольниковСкачать

Определения

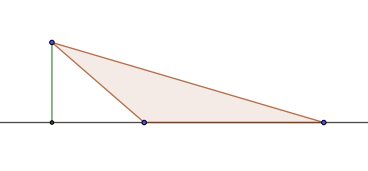
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном это обычный треугольник и подход к решению таких фигур ничем не отличается.

Рис. 1. Тупоугольный треугольник.

В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.

Рис. 2. Высота в тупоугольном треугольнике.

Только в тупоугольном треугольнике высота может лежать за пределами треугольника.

Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.

Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

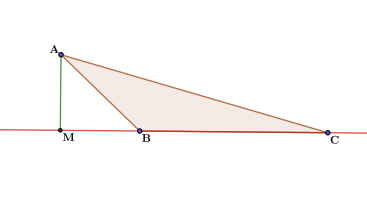
Пример решения задачи

Рис. 3. Рисунок к задаче.

Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.

Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.

• Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.

Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.

• Второй способ это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем через значение косинуса найти значение синуса того же угла. А синус это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза это сторона АВ прямоугольного треугольника.

Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.

• Третий метод это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.

$$sqrt =sqrt =sqrt =3sqrt $$ – по теореме косинусов.

Значение синуса угла АВС определим по основному тригонометрическому тождеству.

Выразим искомый синус угла АСВ.

Выразим из треугольника АМС и найденного значения синуса сторону АМ.

Ответы всех трех способов совпали, а значит задача решена верно.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Что мы узнали?

Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а так же выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.

Видео:32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Тест по теме

Оценка статьи

Средняя оценка: 4.6 . Всего получено оценок: 134.

Не понравилось? — Напиши в комментариях, чего не хватает.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Содержание

1. Определения
2. Пример решения задачи
3. Что мы узнали?

Бонус

Тест по теме

• Площадь прямоугольного треугольника
• Высота треугольника
• Площадь правильного треугольника
• Площадь прямого треугольника
• Площадь равностороннего треугольника
• Площадь равнобедренного треугольника
• Медиана треугольника
• Правильный треугольник Тупоугольный треугольник
• Остроугольный треугольник
• Свойства прямоугольного треугольника
• Стороны прямоугольного треугольника
• Средняя линия прямоугольного треугольника
• Признаки подобия прямоугольных треугольников
• Высота равностороннего треугольника
• Медиана равностороннего треугольника
• Неравенство треугольника
• Длина медианы правильного треугольника
• Равнобедренный тупоугольный треугольник
• Средняя линия прямоугольного треугольника
• Длина средней линии треугольника

По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.

1. 1. Михаил Тяпин 214
2. 2. Наталия Дробот 198
3. 3. Мария Кауфман 192
4. 4. Игорь Проскуренко 157
5. 5. Соня Зверева 153
6. 6. Василиса Варавкина 119
7. 7. Иоанн Стефановский 107
8. 8. Софья Холена 94
9. 9. Оля Проскурина 85
10. 10. Татьяна Бежина 83

1. 1. Мария Николаевна 13,500
2. 2. Лариса Самодурова 12,695
3. 3. Liza 12,310
4. 4. Кристина Волосочева 11,445
5. 5. TorkMen 11,441
6. 6. Ekaterina 11,176
7. 7. Влад Лубенков 11,100
8. 8. Лиса 11,070
9. 9. Юлия Бронникова 11,060
10. 10. Вячеслав 10,840

Самые активные участники недели:

• 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
• 2. Николай З — подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим виды треугольников и научимся строить прямоугольный треугольник на нелинованной бумаге. Вначале вспомним определение треугольника и его элементы, какие существуют виды углов, узнаем, как на нелинованной бумаге построить прямой угол. Далее узнаем, как делятся треугольники на виды в зависимости от типа углов в них. Рассмотрим несколько задач на нахождение вида треугольников и на построение

Видео:Равнобедренный треугольник. 7 класс.Скачать

Треугольник и его элементы

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и трех соединяющих их отрезков. В любом треугольнике различают следующие элементы:

Вершины (рис. 1). Это точки.

Рис. 1. Элементы треугольника: вершины

Стороны (Рис. 2). Это отрезки.

Рис. 2. Элементы треугольника: стороны

Рис. 3. Элементы треугольника: углы

Видео:Виды треугольников: остроугольный, прямоугольный ,тупоугольный. Как начертить треугольникСкачать

Виды углов

Развернутый угол. (Рис. 4)

Угол называется развернутым, если его стороны лежат на одной прямой.

Рис. 4. Виды углов: развернутый

Прямой угол (Рис. 5)

Прямой угол составляет половину развернутого.

Рис. 5. Виды углов: прямой угол

Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.

Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).

Рис. 5. Модель угла и угол на чертеже

Рис. 6. Модель угла, приложенная к углу на чертеже

Мы убедились, что на чертеже действительно изображен прямой угол.

Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).

Рис. 7. Прямоугольный треугольник

Непрямые углы делятся на острые (Рис. 8) и тупые (Рис. 11).

Рис. 8. Виды углов: острый угол

Острый угол меньше прямого (Рис. 10).

Рис. 10. Сравнение острого и прямого угла

Рис. 11. Виды углов: тупой угол

Тупой угол больше прямого (Рис. 12).

Рис. 12. Сравнение тупого и прямого угла

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

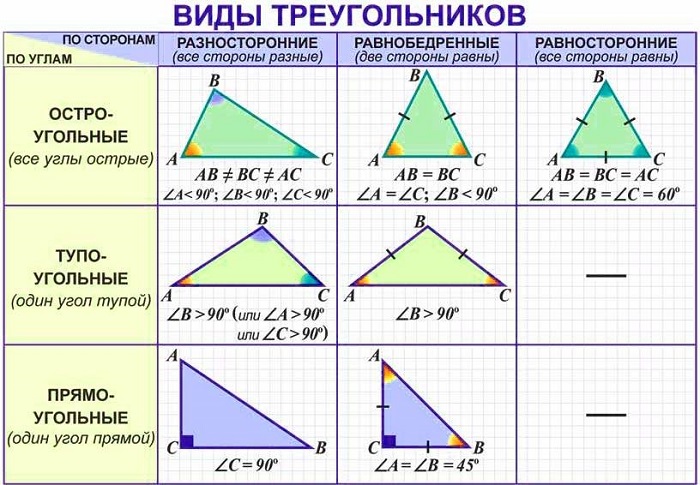
Виды треугольников

Прямоугольный треугольник (Рис. 13). Угол – прямой.

Рис. 13. Виды треугольников: прямоугольный треугольник

Остроугольный треугольник (Рис. 14). Все углы данного треугольника острые.

Рис. 14. Виды треугольников: остроугольный треугольник

Тупоугольный треугольник (Рис. 15). Угол – тупой.

Рис. 15. Виды треугольников: тупоугольный треугольник

Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Задание 1 (определение вида треугольников)

Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.

Рис. 16. Иллюстрация к заданию 1

Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).

Рис. 17. Проверка треугольника номер 2

Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.

Видео:Построение медианы в треугольникеСкачать

Задание 2 (построение прямоугольного треугольника)

Постройте на нелинованной бумаге треугольник – 20 см.

Построим точку (Рис. 18).

Рис. 18. Точка

Проведем через точку прямую (Рис. 19).

Рис. 19. Прямая, проведенная через точку

Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.

Рис. 20. Построение прямого угла

Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).

Рис. 21. Полученный прямой угол

Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).

Рис. 22. Отрезок

Построим отрезок , который равен 20 см (Рис. 23).

Рис. 23. Отрезок

Соединим полученные точки отрезком см.

Рис. 24. Треугольник

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Виды треугольников в зависимости от длины сторон

В зависимости от длины сторон можно выделить разносторонние и равнобедренные треугольники. Вспомним, если у треугольника длины всех сторон различные, то такой треугольник называется разносторонним. Если в треугольнике две стороны по длине равны, то такой треугольник называется равнобедренным, а равные по длине стороны называют боковыми сторонами треугольника, а третья сторона называется основанием треугольника.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Задание 3 (построение прямоугольного равнобедренного треугольника и прямоугольника)

Постройте равнобедренный треугольник по 20 см. Дополните этот треугольник до прямоугольника.

Построим точку (Рис. 25).

Рис. 25. Точка

Проведем через точку прямую (Рис. 26).

Рис. 26. Прямая, проведенная через точку

Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим прямоугольный треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон треугольника – с лучом (Рис. 27).

Рис. 27. Построение прямого угла

Построим по второй стороне прямого угла луч из точки . Получим прямой угол (Рис. 28).

Рис. 28. Прямой угол

Выполним построение сторон треугольника. Отложим на каждом луче отрезок, равный 20 см, и обозначим точки буквами (Рис. 29).

Рис. 29. Стороны будущего треугольника

Соединим полученные точки отрезком (Рис. 29). Мы получили прямоугольный треугольник по 20 см.

Рис. 29. Треугольник

Выполним вторую часть задания: достроим этот треугольник до прямоугольника. В прямоугольнике все углы прямые. Построим прямой угол с вершиной (Рис. 30).

Рис. 30. Построение прямого угла с вершиной

Проведем луч из точки по второй стороне треугольника (Рис. 31).

Рис. 31. Луч из точки

У прямоугольника противоположные стороны равны. Отложим отрезок на новом луче, который равен по длине отрезку (Рис. 32).

Рис. 32. Построение стороны

Соединим точки (Рис. 33).

Рис. 33. Прямоугольник

Обратите внимание, в прямоугольнике все стороны равны, значит, получился квадрат (Рис. 34).

Рис. 34. Полученный квадрат

Видео:Построение высоты в треугольникеСкачать

Заключение

Мы сегодня познакомились с видами треугольников: остроугольным, тупоугольным и прямоугольным, и учились строить прямоугольный треугольник на нелинованной бумаге с помощью инструмента «прямоугольный треугольник».

Список литературы

1. Петерсон Л.Г. Математика. 4 класс. Учебник в 3 ч. – М.: 2013. – 96 с. + 128 с. +96 с.
2. Демидова Т.Е., Козлова С.А., Тонких А.П. Математика. 4 класс. Учебник в 3 ч. . 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.
3. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Постройте на нелинованной бумаге прямоугольный треугольник см. Какой вид имеет такой треугольник?
2. Сколько на рисунке треугольников? Сколько из них прямоугольных?
   
3. Задача на смекалку.
4. Нильс летел в своей стае на спине гуся Мартина. Он обратил внимание, что построение стаи напоминает треугольник: впереди вожак, затем два гуся, в третьем ряду три и т. д. Стая остановилась на ночлег на льдине. Нильс увидел, что расположение гусей на этот раз напоминает квадрат, состоящий из рядов, в каждом ряду – одинаковое количество гусей, причем число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50. Сколько гусей в стае?

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Остроугольный треугольник — виды, свойства и признаки

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

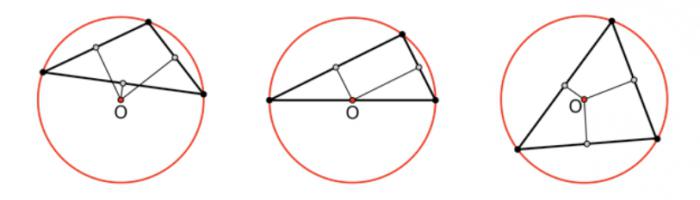
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

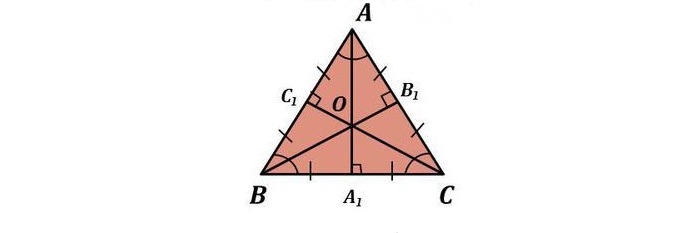
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

2. Высоты пересекаются в одной точке, образуя ортоцентр.

3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

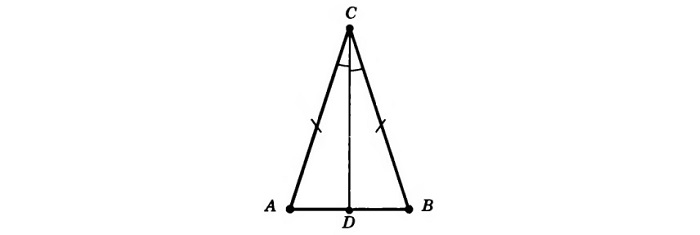
Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

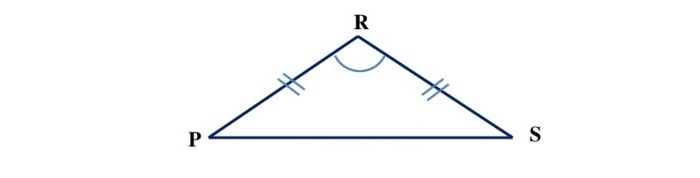
Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.