Момент сопротивления прямоугольного треугольника

Что такое момент сопротивления и откуда взялся этот термин? Каждое тело, даже элементарно малое, имеет определенную массу, геометрические и прочностные характеристики, т.е. обязательно имеет центр тяжести и сопротивляется растяжению или сжатию. Эти прочностные характеристики называются сопротивлением материала сжатию или растяжению. Значение сопротивления зависит от физических свойств тела и пока нами не рассматривается. На данном этапе достаточно знать, что сталь намного прочнее бумаги, а на сколько прочнее — дают ответ различные справочники.

Когда мы определяли момент сопротивления для поперечного сечения балки из однородного материала, обладающего изотропными свойствами, то вывели следующие расчетные формулы:

W ≥ М / R (149:4.8)

где М — максимальный изгибающий момент, определяемый по эпюре моментов. На действие максимального момента и рассчитывается поперечное сечение,

R — расчетное сопротивление, определяемое по разного рода справочникам, впрочем при сильном желании приблизительно определить расчетное сопротивление можно и самому, обычно расчетное сопротивление находится близко к пределу упругости. Т.е. предполагается работа материала в области упругих (восстанавливаемых со временем) деформаций.

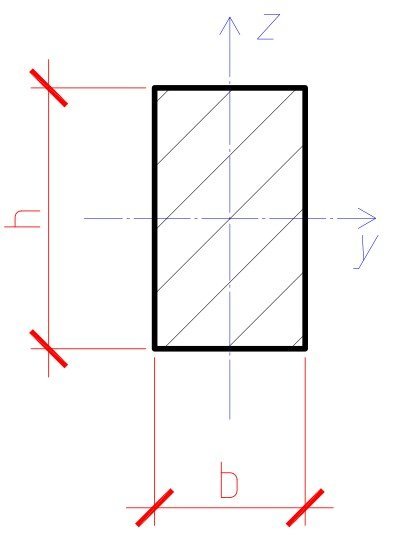
W — момент сопротивления. Для прямоугольного сечения:

W_z = b · h 2 / 6 (149:4.6)

где b — ширина балки, h — высота балки.

Однако строительные конструкции далеко не всегда имеют прямоугольную форму, простую геометрическую форму или форму прокатного профиля, моменты сопротивления для которых давно рассчитаны другими. Кроме того материал, из которого сделана конструкция, может обладать разными расчетными сопротивлениями при сжатии и при растяжении, например, бетон или железобетон, и далеко не всегда материал является изотропным при действии нормальных и касательных напряжений, например, древесина. Поэтому при решении различных задач по расчету строительных конструкций иногда приходится определять момент инерции для поперечного сечения самому. Рассмотрим наиболее распространенные случаи, когда это требуется:

1. Момент сопротивления для прямоугольного сечения анизотропного материала.

Для определения параметров прямоугольного сечения анизотропных материалов, таких как бетон, железобетон, других композитных материалов с различными расчетными сопротивлениями на растяжение и сжатие, момент сопротивления следует определять отдельно для сжимаемой и для растягиваемой зоны или производить расчеты для приведенного сечения. Пока рассмотрим, что получается, при определении параметров отдельно для сжимаемой и для растягиваемой зоны. Из общего уравнения (149:4.8) мы можем простейшим математическим действием, каковым является умножение, вывести следующее уравнение:

M = WR (1.1)

Это общее уравнение, безусловно справедливое для прямоугольного сечения изотропного материала, его еще можно записать следующим образом:

M = (W_с + W_р) R / 2 (1.2)

где нижние индексы _с и _р — условные обозначения для сжатия и растяжения.

при W_с = W_р = W_z и при R_с = R_р уравнения (1.2) или (1.3) сводятся к (1.1). А на 2 мы делим уравнения потому, что моменты сопротивления определяются для всего сечения, а не для сжимаемой или растягиваемой части. Впрочем, этой двойке можно дать и другое толкование.

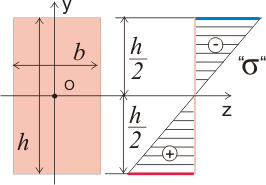
Согласно теории сопротивления материалов нормальные сжимающие и растягивающие напряжения распределяются по высоте балки не равномерно. При определенном действии изгибающего момента максимальные сжимающие напряжения возникают в верхнем слое поперечного сечения (на рисунке 1 обозначены синим цветом), а максимальные растягивающие напряжения — в нижнем слое поперечного сечения (на рисунке 1 обозначены красным цветом), а в центральной части — на оси z, проходящей через центр тяжести сечения, нормальные напряжения равны 0:

Рисунок 1. Эпюра нормальных напряжений, возникающих в поперечном сечении при действии изгибающего момента.

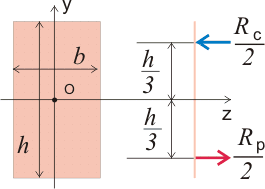
С точки зрения строительной механики для упрощения расчетов вполне допустимо заменить распределенную нагрузку, каковой в данном случае является эпюра нормальных напряжений, сосредоточенными силами, равнодействующими для каждой части эпюры:

Рисунок 2. Замена распределенной нагрузки сосредоточенной нагрузкой.

В данном случае сосредоточенные силы можно рассматривать как расчетные сопротивления R, приложенные ко всей площади сечения сжатой или растянутой зоны с плечом h/3, а так как равнодействующая сила от равномерно изменяющейся нагрузки, в данном случае нормальных напряжений σ, будет равна половине нагрузки, умноженной на длину приложения нагрузки, то мы можем рассматривать значения R_с/2 и R_р/2, чтобы соблюдалось условие σ ≤ R.

Вне зависимости от того, каким является материал, можно допустить, что конструкция из этого материала будет работать нормально, если соблюдается следующее условие:

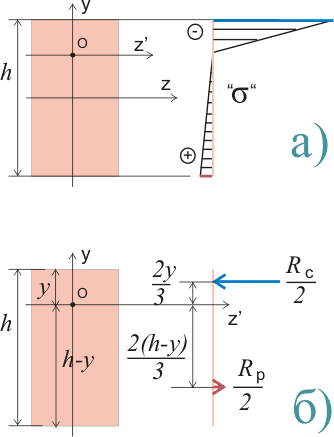
Если считать, что распределение внутренних нормальных напряжений всегда происходит относительно центра тяжести сечения, так как показано на рисунке 1, то расчет параметров сечения следует производить по наименьшему расчетному сопротивлению. Но если мы допустим, что центр тяжести сечения может смещаться, то для анизотропного материала, например бетона, для которого сопротивление сжатию приблизительно в 10 раз больше сопротивления растяжению, эпюра предельных нормальных напряжений может выглядеть следующим образом:

Рисунок 3. Эпюра нормальных напряжений и приведенные сосредоточенные нагрузки для приведенного сечения.

При этом центр тяжести приведенного сечения сместится и будет находиться на оси z’. Поэтому значения моментов сопротивления будут:

W_с = 2by 2 / 3 (1.5.1)

W_р = 2b(h -y) 2 / 3 (1.5.2)

Примечание: так как мы рассматриваем не просто верхнюю сжатую или нижнюю растянутую часть сечения, а условно сжатое сечение и условно растянутое сечение, то правые части уравнений (1.5.1) и (1.5.2) следует умножить на 2, чтобы учесть и верхнюю и нижнюю часть условного сечения, а затем разделить на 2, чтобы учесть, что напряжения по высоте полусечения изменяются от максимума до 0. Впрочем, на конечном результате это никак не отразится.

Подставляя эти значения в уравнение (1.4), получим:

таким образом соотношение высоты сжатой у и растянутой зоны (h -y) для материала с анизотропными свойствами зависит от соотношения расчетных сопротивлений в степени 1/2.

Решая дальше уравнение (1.7), мы получим значение

В принципе эту формулу можно использовать и для изотропного материала, у которого расчетные сопротивления растяжению и сжатию равны. В этом случае мы получим у = h / (√‾1 +1) = h / 2.

Определить значение у, можно и другим способом, если мы не знаем значение высоты элемента (да и откуда нам его знать, если как правило мы должны определить высоту в результате расчетов), но знаем значение максимального изгибающего момента. Согласно формул (1.4) и (1.5.1)

Теперь, чтобы эти формулы не остались абстрактными измышлениями, применим их на практике:

Пример расчета бетонного элемента прямоугольной формы на действие изгибающего момента.

На бетонную плиту перекрытия с расчетной шириной b = 100 см будет действовать изгибающий момент М = 180000 кг·см (от нагрузки 900 кг/м при пролете шарнирно опертой плиты l = 4 м). Для изготовления плиты будет использован бетон класса В20 с расчетным сопротивлением сжатию R_b = 117 кг/см 2 и расчетным сопротивлением растяжению R_bt = 9.2 кг/см 2 . Требуется определить высоту сжатой и растягиваемой зоны. Согласно полученных нами формул

у = √ (3·180000 /2·100·117 = 4.8038 см

h = 4.8038·(√ 117/9.2 + 1) = 21.9348 см или 22 см.

Как видим расчет в данном случае достаточно прост и нагляден. Единственное, что нас может в данном случае беспокоить, это то, что нагрузка на плиту от собственного веса будет составлять до 550 кг/м, т.е. почти две трети от расчетной нагрузки. И кроме того приведенный центр тяжести сечения так сильно не может смещаться относительно центра тяжести без дополнительного перераспределения напряжений, ведь мы все-таки рассматриваем балку из одного материала и значит высота балки должна быть как минимум (21.93 — 4.8)2 = 34.3 см. Для того, чтобы увеличить эффективность использования бетона люди и придумали вставлять в бетон арматуру.

2. Момент сопротивления для приведенного сечения анизотропного материала.

Теперь рассмотрим полученные результаты с точки зрения классического изложения понятий о моменте сопротивления. Такое изложение носит достаточно абстрактный характер при отсутствии у студентов понимания, зачем этот самый момент сопротивления нужен. Поэтому я сначала показал практическое применение момента сопротивления, а теперь можно уже переходить к теоретической части. Итак:

Что такое момент сопротивления и откуда взялся этот термин? Каждое тело, даже элементарно малое, имеет определенную массу, геометрические и прочностные характеристики, т.е. обязательно имеет центр тяжести и сопротивляется растяжению или сжатию. Эти прочностные характеристики называются сопротивлением материала сжатию или растяжению. Значение сопротивления зависит от физических свойств тела и пока нами не рассматривается. На данном этапе достаточно знать, что сталь намного прочнее бумаги, а на сколько прочнее — дают ответ различные справочники.

Центр тяжести тела — это точка, относительно которой сумма сил тяжести, действующих на элементарно малые части рассматриваемого тела будет = 0

Причем нахождением центра тяжести мы занимались еще в школе на уроках физики, не имея ни малейшего представления о теории сопротивления материалов, потому как центр тяжести — это понятие общее для всех разделов физики. Для этого мы брали деревянную линейку и пытались опереть линейку на кончик шариковой ручки так, чтобы линейка не падала, т.е. чтобы ни одна из частей линейки не перевешивала другую. Таким образом мы искали центр тяжести сечения с шириной, равной ширине линейки, и высотой, равной длине линейки, при этом одни опирали линейку на пересечение диагоналей линейки, другие на пересечение высоты и ширины, проведенных посредине прямоугольника. Однако толку от этого было мало, так как шарик ручки имеет очень малую площадь, стремящуюся к нулю, то центр тяжести линейки из-за анизотропности материала линейки редко приходился на пересечение указанных линий и потому не попадал на подставленный шарик и линейка почти всегда падала. Чтобы решить задачу в поставленном виде, пришлось бы провести большое количество вычислений, и все равно возможная погрешность в результатах свела бы эти расчеты к нулю. А если немного изменить условие задачи и опереть линейку на палец в точке предполагаемого центра тяжести, то есть изменить площадь опирания линейки так, чтобы центр тяжести линейки попадал в эту площадь опирания, то линейка достаточно надежно будет держаться на пальце. В данном случае смена опор — это пример того, как можно значительно упростить решение задачи, немного изменив условия. И хотя я являюсь неизменным сторонником простых способов решения задач, без понятия о центре тяжести сечения нам все же не обойтись.

Кстати еще одним способом упрощения решения задачи является рассмотрение не всего тела, а только одного его сечения, таким образом трехмерность окружающего нас объемного мира с его сложностями и неопределенностями заменяется двухмерностью плоскости (плоской фигуры), также имеющей неопределенности, но как минимум на одну меньше. Так как все физические тела имеют некую плотность (которая может обозначаться также как удельный или объемный вес, то для определения массы тела обычно умножают плотность тела на объем тела, который в свою очередь характеризуется такими параметрами как длина ширина и высота. Если рассматривать не все тело, а только некоторое сечение, очень-очень тонкое, т.е имеющее бесконечно малую длину (если вы видели слайсер, а тем более им пользовались, то приблизительно понимаете, что это означает), и постоянную плотность, то с математической точки зрения вполне корректным будет предположение, что

центр тяжести сечения — это точка, относительно которой сумма элементарных площадей сечения, умноженных на расстояния от центра тяжести элементарного сечения до центра тяжести, будет = 0 :

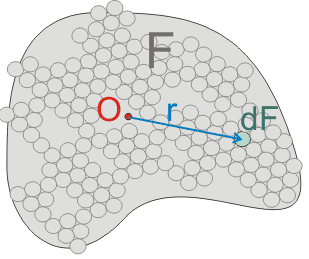
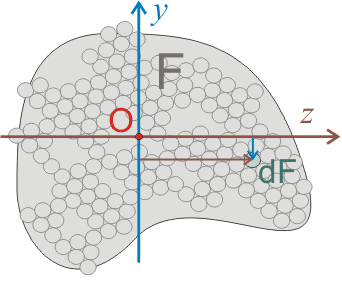
Рисунок 4. Центр тяжести условного сечения, имеющего площадь F.

На рисунке 4 показано некое условное сечение, имеющее площадь F. При этом площадь F — это сумма элементарных площадей dF (одна из этих площадей для наглядности выделена зеленым цветом):

F = ∑dF (2.1.1)

Если есть очень много свободного времени, то никто не запрещает измерить расстояния r от каждой элементарной площади dF до центра тяжести O сечения F. А затем полученные значения перемножить и сложить, проверив соблюдается ли условие. Однако знания математики позволяют сделать это намного быстрее и проще:

Из этого, казалось бы не сложного уравнения следует очень много выводов, например:

1. Если центр тяжести сечения является единственной достаточной точкой опоры для того, чтобы сечение оставалось в статическом состоянии, т.е в состоянии равновесия, то точки, лежащие на одной прямой, проходящей через центр тяжести сечения, также будут надежной опорой для сечения. Причем таких прямых можно провести бесконечно много. Однако нам много не надо, нам достаточно для начала хотя бы двух перпендикулярных прямых. А еще эти прямые можно считать осями координат и тогда задача еще более упростится, так как использование прямоугольной системы координат нам более привычно, чем радиальной. Обычно для определения параметров сечения используются оси х и у. Однако в данном случае мы имеем дело со строительной механикой и теорией сопротивления материалов. Строительная механика решает множество задач, в которых очень важное значение имеет длина конструкции при этом решение сводится к определению внутренних напряжений в различных поперечных сечениях, расположенных на расстоянии х от начала конструкции, т.е. от начала координат, поэтому более корректным мне кажется использование осей у и z для поперечных сечений:

Рисунок 5. Центр тяжести сечения, являющийся началом координат

2. В этом случае справедливыми будут следующие утверждения:

где S_z и S_y — статические моменты сечения относительно главных осей. В данном случае статические моменты сечения равны нулю, это означает, что сечение находится в состоянии статического равновесия. Проверить это теоретическое положение достаточно просто, воспользовавшись все той же линейкой. Если опирать линейку не на кончик пальца, а на весь максимально выровненный палец, символизирующий прямую или ось, то если ось пальца условно говоря проходит через центр тяжести линейки, то линейка не упадет. Причем таких положений линейки может быть достаточно много, достаточно вращать линейку относительно центра тяжести на вытянутом пальце, чтобы в этом убедиться.

Однако оси координат далеко не всегда проходят через центр тяжести сечения и в этих случаях статические моменты относительно главных осей не равны нулю, проще говоря линейка, если линия опоры не проходит через центр тяжести, обязательно упадет, при этом чем дальше будет линия опоры (ось координат) тем большая сила потребуется, чтобы остановить это падение. Вот эту самую силу и ее направление некоторым образом и характеризуют статические моменты. Если известна площадь сечения и положение центра тяжести сечения, при этом оси координат через центр тяжести сечения не проходят, то статические моменты будут равны:

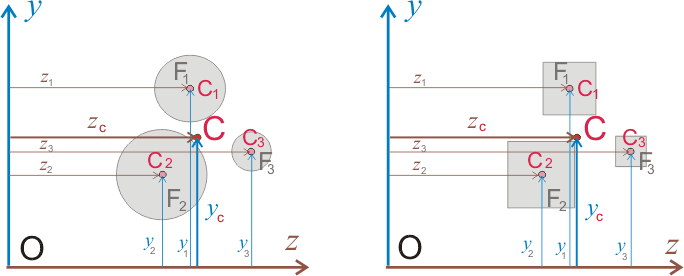
3. Статические моменты сечения или как их иногда называют, статические моменты площади, благодаря описанным выше свойствам, позволяют определить центр тяжести сечения любой геометрической сложности. Для этого сначала задается система координат с началом в произвольной точке, затем сложное сечение разбивается на простые, для которых определить центр тяжести достаточно легко, а после этого из преобразованных формул (2.1.5) и (2.1.6) определяется расстояние от центра тяжести сечения до начала координат:

Рисунок 6. Определение центра тяжести сложного сечения при известных площадях и центрах тяжести простых сечений.

Но не будем слишком долго задерживаться на полезных свойствах статических моментов, ведь в данном случае нас интересует немного другой момент, а именно момент сопротивления. И статический момент и момент сопротивления измеряются в см 3 , но разница между ними есть и разница существенная. Если коротко охарактеризовать разницу между статическим моментом и моментом сопротивления, то статический момент позволяет определить, где находится центр тяжести площади, который и является точкой приложения сосредоточенной нагрузки — массы тела, а момент сопротивления позволяет определить, где находится точка приложения сосредоточенной нагрузки — нормальных сжимающих или растягивающих напряжений, возникающих в поперечном сечении. Другими словами, масса — это равномерно распределенная нагрузка, представляемая на эпюрах прямоугольниками, а нормальные напряжения — это равномерно изменяющаяся нагрузка от 0 в центре тяжести сечения до максимального значения в максимально удаленной точке сечения, представляемая на эпюрах треугольниками (рис. 1). Ну а теперь более подробно:

Одним из предметов исследования теории сопротивления материалов является поперечное сечение тела, часто перпендикулярное оси х, в котором возникают растягивающие и сжимающие напряжения. Основой расчета является принцип равновесия сил, обеспечивающий равновесие тела или, другими словами, геометрическую неизменяемость системы (статическое равновесие). Когда мы опирали линейку на шарик ручки или на палец, мы таким образом приводили систему сил в равновесие. Когда мы пытались опереть деревянную линейку на шарик ручки в центре тяжести, то мы тем самым пытались передать линейке в этой точке сосредоточенную нагрузку, численно равную распределенной нагрузке — весу линейки. Эта сосредоточенная нагрузка, является с одной стороны опорной реакцией, обеспечивающей равновесие сил, а с другой стороны, если свести площадь опирания к максимально возможному минимуму, т.е. использовать в качестве опоры острую иголку, то при достаточно большом весе линейки иголка ее проколет. Произойдет это потому, что мы преодолеем предел прочности линейки. Т.е. сопротивление сжатию материала будет меньше приложенной сосредоточенной нагрузки. Сопротивление материала сжатию или растяжению измеряется в Н/м 2 или кгс/см 2 и таким образом показывает какую максимальную нагрузку можно приложить к указанной площади сечения. Поэтому когда мы уменьшаем площадь сечения опоры, мы тем самым увеличиваем нагрузку в месте ее воздействия. Таким образом при расчете параметров сечения, к которому нагрузка приложена в центре тяжести, достаточно знать расчетное сопротивление материала, чтобы определить требуемую площадь сечения:

F = N / R (2.2)

Эту площадь можно называть площадью сопротивления.

Примечание: Обозначений для площади существует несколько: S, F, A. Если обозначать площадь литерой S, то будут возникать аллюзии со статическим моментом или с энтропией; если А, то с амплитудой, работой и даже с ангстемом; если F, то с силой, а еще с прогибом. Дело в том, что для обозначения различных величин, открытых и применяемых в последние годы человечеством не хватает букв не только латинского, но и греческого алфавита, а общие тенденции развития науки говорят о том, что единственным спасением в этом деле смогут стать только иероглифы. Так как по ходу дела мы уже столкнулись со статическими моментами, то примем обозначение для площади F.

Однако нагрузка в поперечном сечении далеко не всегда прикладывается к центру тяжести сечения. Таким образом появляется плечо действия силы или пары сил и значит в рассматриваемом поперечном сечении может действовать не только сила, но и изгибающий момент, а при чистом изгибе только изгибающий момент. В ответ на это в материале возникает другой момент, направленный противоположно, и, исходя из условий равновесия, равный изгибающему моменту. А значит плечо действия ответного момента равно плечу действующего момента и тогда ответный момент логично названный «моментом сопротивления» равен равнодействующей нормальных напряжений, умноженной на плечо действия силы, в данном случае сопротивления материала (или пары сил, создающих момент относительно центра тяжести). Что и приводит нас к формуле (149:4.3). Даже графически обозначение момента сопротивления W является как бы зеркальным отражением изгибающего момента M. Это особенно заметно по следующей формуле:

(2.2.2)

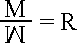
Анизотропный материал можно рассматривать как множество соединенных между собой тел. При этом каждое тело может обладать своими геометрическими и прочностными характеристиками. Таким образом каждое такое тело может рассматриваться как самостоятельное, однако при этом необходимо учитывать расстояние от центра тяжести данного тела до центра тяжести общего сечения:

W_{сечения тела} + F_{сечения} · плечо (расстояние от центра тяжести рассматриваемого сечения до общего центра тяжести) (2.3)

Далее, используя интегрирование, мы можем определить момент сопротивления для сечения практически любой геометрической формы и удаленного от общего центра тяжести на любые расстояния. В данном случае у нас нет необходимости это делать. Как говорил один известный персонаж: «ничего воровать не надо, все уже украдено до нас». Поэтому при расчетах простых геометрических сечений мы можем пользоваться готовыми формулами. Но для наглядности приведу один пример, задача для элементарного прямоугольного сечения, входящего в состав общего сечения так, что общий центр тяжести находится на нижней грани элементарного сечения, решается так (эту задачу мы доступными нам на тот момент средствами решали в п.1 — формула (1.5.1)):

W_c = W_{прямоугольника} + F_{прямоугольника} · плечо (половина высоты) = bh 2 /6 + bh·h/2 = 2bh 2 / 3 (2.3.1)

Как видим, окончательный результат остался таким же.

Теперь вооруженные полученными знаниями, мы можем решать более сложные задачи, например попробовать определить момент сопротивления для железобетонной конструкции и вскоре узнаем, что произойдет, если в нижнюю растягиваемую зону поперечного сечения плиты, рассматриваемой в качестве примера в п.1, добавить стальную арматуру.

Бетон, при добавлении в него арматуры становится еще более анизотропным материалом, и оттого расчет железобетонной конструкции становится еще более веселым. Для начала: в растягиваемой зоне поперечного сечения устанавливается арматура, имеющая приблизительно в 100 раз большее расчетное сопротивление растяжению, чем бетон. К тому же арматура устанавливается как можно ближе к низу сечения, это позволяет использовать прочностные свойства арматуры почти по максимуму. Ставить арматуру в самом низу сечения не позволяют конструктивные соображения. Дело в том, что для того, чтобы рассматривать арматуру, как часть общего сечения, арматура должна быть как следует обжата бетоном, для этого в частности на арматуре делаются ребра. Арматура считается достаточно обжатой, когда расстояние от низа сечения арматуры до низа сечения конструкции составляет не менее диаметра арматуры или не менее 10 мм. А еще бетон под арматурой защищает арматуру от атмосферных воздействий, проще говоря, не дает арматуре ржаветь и таким образом препятствует уменьшению расчетного сечения арматуры. Для упрощения расчетов железобетонных конструкций используется величина а — расстояние от центра тяжести арматуры до низа сечения конструкции. Принимается эта величина так, чтобы соблюдалось приведенное выше условие. Соответственно высота поперечного сечения теряет актуальность и в расчетах больше используется другая величина h₀ = h — a.

Пример расчета железобетонного элемента на действие изгибающего момента .

При расчете железобетонных конструкций можно пользоваться следующими расчетными предпосылками:

1. Так как арматура, устанавливаемая в растягиваемой зоне бетона, имеет намного большее сопротивление растяжению, чем бетон, то сопротивление бетона растяжению для упрощения расчетов можно не учитывать. Таким образом мы повышаем прочность конструкции на 0.3-1%

2. Обычно моментом сопротивления арматуры относительно собственного центра тяжести, как относительно малой величиной по сравнению с моментом сопротивления относительно общего центра тяжести, для упрощения расчетов пренебрегают, тогда момент сопротивления арматуры будет составлять:

Примечание: В данном случае мы также рассматриваем не просто растянутую часть поперечного сечения, а некое условное сечение, в котором и в верхней и в нижней части действуют растягивающие напряжения, поэтому для определения момента сопротивления правую часть уравнения нужно умножить на 2. А так как диаметр арматуры мал по сравнению с расстоянием от центра тяжести арматуры до центра тяжести сечения, то мы можем допустить, что растягивающие напряжения, возникающие в арматуры постоянны по высоте сечения арматуры и максимальны, а это означает, что делить правую часть уравнения на 2, как при определении момента сопротивления сжатой части, не нужно.

3. При использовании арматуры класса А400 с расчетным сопротивлением растяжению R_р, в последнее время все чаще обозначаемым как R_s = 3600 кг/см 2 (но я далее буду придерживаться обозначения R_a, чтобы было понятно, что это арматура):

Если продолжать рассматривать работу конструкции в области упругих деформаций, то для бетона, работающего в сжатой области, значение у можно принимать такое же как и в п.1, и тогда мы можем подобрать сечение арматуры при заданной высоте сечения, например при h = 10 см, а = 2 см, h₀ = 8 см.

F_a = 180000 /2(3600(8 — 4.8038)) = 7.82 см 2

Для армирования плиты перекрытия достаточно 5 стержней диаметром 16 мм, имеющих суммарную площадь F = 10.05 см 2 .

Такой расчет называется расчетом по допускаемым напряжениям, предполагает упругую модель деформации тела и в настоящее время для расчета железобетонных конструкций не используется.

В настоящее время расчет выполняется по предельным состояниям, учитывающим пластическую работу материала и основанным в частности на результатах многочисленных испытаний железобетонных конструкций. При расчете по многократно проверенным и принятым в ранее и ныне действующих СНиПах и сводах правил способам необходимое сечение арматуры для такой плиты перекрытия будет составлять около 7.27 см 2 , т.е. немного меньше полученного нами результата (но зато позволяет принять для армирования стержни меньшего диаметра, что при больших объемах строительства может дать ощутимую экономию).

Устранить эту разницу можно, принимая основные положения расчета ж/б конструкций по предельным состояниям, т.е. допуская в сжатой зоне бетона образование пластического шарнира, и возникающее при этом перераспределение напряжений и соответственно уменьшение высоты сжатой зоны бетона. Однако я не советую делать это при расчетах конструкций частного малоэтажного строительства. Дело в том, что все равно потребуется расчет по деформациям, а как показывает практика, для шарнирно опертых балок деформации превышают допустимые. К тому же высота защитного слоя является недопустимой при таком диаметре арматуры и по хорошему плиту нужно пересчитывать на h_o = 7 см, или увеличить высоту плиты, но пока этого делать не будем.

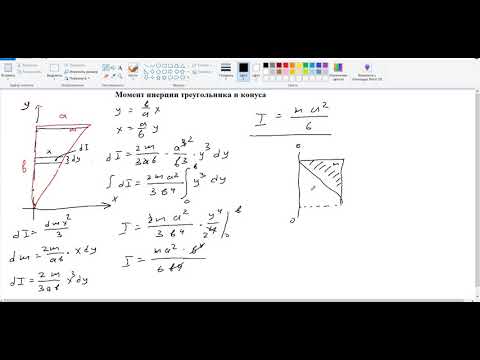
Пример приближенного расчета прогиба железобетонной плиты (расчет по предельным состояниям второй группы)

Одним из главных достоинств вышеизложенной методики расчета является то, что зная фактическую высоту сжатой зоны бетона, мы можем приблизительно, повторяю — приблизительно, т.е. без учета особенностей работы бетона и арматуры — но довольно быстро определить прогиб конструкции. При точном расчете необходимо рассчитывать отдельно участки конструкции без трещин и участки с раскрытыми трещинами, но как показывает практика, даже такой расчет не всегда точен. В данном случае мы проведем приближенный, так называемый оценочный расчет. Основан такой расчет на следующих предпосылках:

1. Так как у нас нет армирования в верхней части плиты, то на сжатие будет работать только бетон и в результате этого сжатия плита деформируется.

2. В нижней части плиты на растяжение работает только арматура. В результате деформации арматуры плита также прогнется.

3. В идеале величина прогиба от деформации сжимаемого бетона и от деформации растягиваемой арматуры должна быть одинаковой.

4. Если величина прогиба будет неодинаковой, то по полученным значениям отдельно для бетона и отдельно для арматуры можно определить некоторое среднее значение прогиба, которое будет приблизительно соответствовать реальному прогибу железобетонной конструкции.

5. Если величина прогиба в результате растяжения арматуры будет больше, чем при сжатии бетона, то допустимо уменьшить высоту сжатой зоны бетона. Это будет означать образование пластического шарнира в сжатой зоне бетона. При этом высота сжатой зоны бетона не может быть уменьшена больше, чем в 1.5 раза, в противном случае высота пластического шарнира станет критической и это может привести к обрушению конструкции. Уменьшать высоту растянутой зоны недопустимо, так как это может привести к обрушению конструкции.

Данные предпосылки позволяют использовать для расчетов стандартные формулы строительной механики для любых вариантов загружения балок. В данном случае мы рассчитывали плиту перекрытия как балку с шарнирными опорами и равномерно распределенной нагрузкой. Для такой балки прогиб поперечного сечения посредине балки составит:

f = 5ql 4 /(384EI) (174.6.4.4)

для бетона Е_b = 275000 кгс/см 2 (27500 МПа) — начальный модуль упругости бетона класса В20.

I_b = W_c·y = 2·100·4.8 3 /3 = 7372,8 см 4 или b(2y) 3 /12 = 100(2·4.8) 3 /12 = 7372.8 см 4 — момент инерции условного приведенного сечения, тогда

f_b = 5·9·400 4 /384·275000·7372.8 = 1.45 см.

Проверим возможный прогиб от растяжения арматуры.

модуль упругости арматуры Е_a = 2000000 кгс/см 2 , (2·10 5 МПа),

условный момент инерции арматуры I_a = 10.05·2·3.2 2 = 205.8 см 4 , тогда

f_a = 5·9·400 4 / 384·2000000·160.8 = 7.9 см

Очевидно, что разным прогиб быть не может, а значит в результате деформации и выравнивания напряжений в сжатой зоне высота сжатой зоны будет уменьшаться. Подробности определения высоты сжатой зоны здесь (из-за недостатка места) не приводятся, при y ≈ 3.5 см прогиб составит примерно 3.2 см. Однако реальный прогиб будет другим, во-первых потому, что мы не учли деформацию бетона при растяжении (потому этот метод и является приблизительным), во вторых, при уменьшении высоты сжатой зоны в бетоне будут нарастать пластические деформации, увеличивающие общий прогиб. А кроме того при длительном приложении нагрузок развитие пластических деформаций также приводит к снижению начального модуля упругости. Определение этих величин — отдельная тема.

Так для бетона класса В20 при длительно действующей нагрузке модуль упругости может уменьшиться в 3.8 раза (при влажности 40-75%). Соответственно прогиб от сжатия бетона составит уже 1.45·3.8 = 5.51 см. И тут даже двойное увеличение сечения арматуры в растянутой зоне сильно не поможет — необходимо увеличивать высоту балки.

Но даже если не учитывать длительность действия нагрузки, то все равно 3.2 см — это достаточно большой прогиб. Согласно СНиП 2.01.07-85 «Нагрузки и воздействия» максимальный допустимый по конструктивным соображениям прогиб для плит перекрытия (чтобы стяжка не растрескивалась и т.п.) составит l/150 = 400/150 = 2.67 см. А так как и толщина защитного слоя бетона по-прежнему остается недопустимой, то из конструктивных соображений высоту плиты следует увеличить хотя бо до 11 см. Впрочем к определению момента сопротивления это никак не относится.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Расчет железобетонных конструкций

Оценка пользователей:13.2 (голосов: 6)Переходов на сайт:62485Комментарии:

Уважаемый Доктор Лом, изучил Ваш материал по прогибу ЖБ плиты (Вы давали мне ссылку из темы «Расчет железобетонной балки» от 12-02-2013). Вопросы:
1. В районе формулы (174.6.4.4).
При расчете момента инерции условного приведенного сечения исходные данные следующие?
I = Wc•y =(2by2/ 3)•y=(2•100•4.82/3)•4.8 =7372,8 см4
В выражении небольшая неточность: fb = 5•9•4004 / 384•275000•7372,8 = 1.45 (1.48) см. (7372,8 вместо 13972.5).
2. Ниже по тексту.
Момент инерции арматуры I = 7.69•3.22 = 78.74 см4,
7,69 — площадь принятого сечения арматуры 14 мм, 5 стежней;
3.2 — что это за число? Очень похоже на а (расстояние от центра тяжести арматуры до низа сечения конструкции). Какая в данном случае формула для расчета момент инерции арматуры?
3. Ниже по тексту.
Для чего в выражении «fa = 5•9•4004 / 2•384•2000000•78,74 = 9.52 см.» в знаменателе число 2?
Не связано ли число 2 с темой «Расчет металлической перемычки для несущих стен», т.к. там рассчитывается прогиб перемычки, состоящей из двух профилей:
«…для 2 профилей это значение логично умножается на 2), тут главное, не ошибиться с осью.
Для перемычки из 2 уголков 110 х70 х 8 мм над проемом 1.5 м прогиб f = (5 x 3167 x 1.54) / (384 x 2 x 1010 х 2 x 171.54 х 10-8) = 0.003045 м или 0.3 см
Для перемычки из 2 швеллеров 8П над проемом 1.5 м прогиб f = (5 x 3167 x 1.54) / (384 x 2 x 1010 х 2 x 89.8 х 10-8) = 0.0058 м или 0.58 см».
4. Вопрос перекочевавший из темы «Расчет железобетонной балки» от 11.02.2013 г.
Если в данном примере (расчет по предельным состояниям второй группы) заменить стальную арматуру композитной (при всех равных других исходных данных), то можно оценить прогиб композитобетонной плиты.
Принимаем модуль упругости композитной арматуры Ек =550 000 кгс/см2, (0,55•10^5 МПа), то
fa = 5•9•4004 / 2•384•550000•78,74 = 34.64 см. В 13 раз боль допустимого. Или если мы хотим получить прогиб близкий к величине 9,52 мм, надо использовать 11 стержней композитной арматуры диаметром 18 мм. Данный расчет близок к правде?
К тому же, я прочитал, что для обеспечения адекватной работы композитной арматуры в бетоне, она (арматура) должна быть в преднапряженном состоянии. Так ли это?
Спасибо.

1. 13972.5 — действительно опечатка — исправил, спасибо за внимательность.
2. 3.2 — это расстояние от центра тяжести арматуры до центра тяжести приведенного сечения, равное ho — y.
3. Нет не связано. В данном случае 2 — в связи с тем, что мы рассчитывали момент сопротивления арматуры по формуле (2.5), т.е. на половину действующего момента или на половину от действующей нагрузки.
4. То, что Вы получили прогиб почти в 4 раза больше для композитной арматуры — логично, т.к. модуль упругости для композитной арматуры почти в 4 раза меньше, чем у стальной арматуры. Именно на это я указывал в предыдущем своем ответе, теперь, ознакомившись с расчетами, Вы понимаете почему.
Чтобы получить такой же прогиб нужно использовать или композитную арматуру сечением почти в 4 раза больше, при этом более рациональным будет увеличение сечения стержней, а не добавление стержней такого же диаметра, или увеличивать высоту балки или принимать для расчетов более прочный бетон.
Любая преднапряженная арматура улучшает характеристики конструкции.
И последнее, данный расчет все равно является приближенным, так сказать, оценочным. Более точный расчет следует производить по требованиям СНиП.

Спасибо, Доктор, все стало на свои места.
Получение преднапряженного состояния арматуры в частном домостроении достаточно непростая задача, я полагаю. А существуют какие-нибудь «народные» способы это сделать? И насколько преднапряженное состояние арматуры улучшает характеристики ЖБИ (если возможно в цифрах)?
Спасибо.

Вообще-то армабетонные конструкции с предварительным напряжением арматуры — тема для отдельной большой статьи, но попробую коротко.
Арматура, как мы уже видели, выдерживает гораздо большие деформации чем бетон, поэтому если при изготовлении конструкции арматуру предварительно растянуть, т.е. деформировать (для этого нужно специальное оборудование), а после достижения бетоном проектной прочности отпустить, то арматура постарается сжаться, а помешает ей сжаться до исходных размеров соответствующим образом выполненная анкеровка. При этом нижний слой конструкци, который под нагрузкой будет растягиваться, сожмется, а верхний слой растянется (поэтому в предварительно напряженных конструкциях необходим и верхний слой арматуры). Таким образом получится подобие арки. Под действием расчетной нагрузки конструкция прогнется до расчетных пределов, преодолев прямолинейное состояние и в окончательном виде напоминая перевернутую арку (когда мы вычисляли прогиб — это и была высота арки). Таким образом в результате преднапряженного состояния создается запас по прочности в 10-15% в зависимости от марки бетона.
Помимо дополнительных расчетов нужна еще и соответсвующая анкеровка преднапряженной арматуры, так что заваривать всю эту кашу ради изготовления двух-трех армокаменных конструкций в домашних условиях явно не стоит. Весь необходимый пакет расчетов может обойтись в несколько раз дороже, чем сами конструкции.
А вот сделать при бетонировании в домашних условиях нечто вроде очень пологой арки никто не мешает. Конечно арку также нужно рассчитывать, да и добавятся дополнительные горизонтальные нагрузки на стены, но все равно сделать это и рассчитать намного проще, чем возиться с преднапряжением арматуры. Конечно же эффект будет тем лучше, чем больше будет высота арки. Так за много тысячелетий до изобретения железобетона люди уже делали перекрытия из камней в виде арки, причем далеко не всегда это были заметные простым глазом арки. А возможно это потому, что в арке благодаря ее форме практически весь материал работает на сжатие и даже арматура по большому счету не нужна, да и прочность арки при должной высоте арки и одинаковой высоте с прямолинейной конструкцией увеличится примерно в два раза т.е. эффект может быть 80-120%.
Почему пологие арки практически не используются в частном домостроении — вопрос. Возможно, тут самым главным ограничителем является высота арки, для перемычек длиной 1-3 м это решающей роли не играет, а на общей высоте перекрытия длиной более 6 метров может сказаться значительно, но так уж устроен мир — ничего идеального в нем нет, во всяком случае с точки зрения человека. Но скорее всего люди просто не знают или не хотят знать о чудесных свойствах арочных конструкций. Когда есть деньги, гораздо проще, да и быстрее по времени купить готовые конструкции или заказать их изготовление специалистам.
(Все равно получилась маленькая статья).

Спасибо за развернутый ответ.

Считаю должным исправить ряд ошибок, в предыдущем тексте.
Естественно изогнутая(изогнутая до нагружения) конструкция называется вспарушенной балкой или оболочкой. В отличии от арки такая конструкция не воспринимает распор(как рессора авто).
Преднапряжение применяется для уменьшения прогибов и, в основном, повышения трещиностойкости конструкции. Ни каких запасов прочности преднапряжение не дает.

1. Текст, в котором вы считаете должным исправить ряд ошибок, адресован человеку, скорее всего слабо разбирающемуся в строительных терминах, а потому написан с максимальной степенью упрощения.
2. Термин «вспарушенный» как раз и означает, что рассматриваемая пластина (оболочка) может рассматриваться как арка в одной или в двух взаимно перпендикулярных плоскостях, а так как вспарушенные своды имеют достаточно сложную геометрическую форму и могут иметь всего 4 точечных опоры, при этом в двух перпендикулярных плоскостях сечение пластины представляет собой ту же арку, то такая конструкция в целом и напоминает парус.
3. Ваше утверждение о том, что вспарушенная конструкция не воспринимает распор, сформулировано некорректно, во-первых потому, что под действием вертикальной нагрузки вспарушенный свод создает (а не воспринимает) распор, т.е. возникают горизонтальные опорные реакции, а вот для восприятия этих горизонтальных реакций и уменьшения передачи горизонтальных нагрузок на опоры делаются кружала или армировочный пояс.
4. По поводу запаса прочности. Вы слишком придираетесь к словам, вырванным из контекста. По смыслу должно быть понятно, что конструкция с предварительно напряженной арматурой может выдержать нагрузку на 10-15% больше, чем такая же конструкция с той же арматурой, но без предварительного напряжения. Конечно, более правильно было бы охарактеризовать это, как «увеличение несущей способности конструкции при использовании предварительного напряжения», я назвал это «запасом прочности». Почему? Смотрите п.1.

Док, пересчитайте пож Пример расчета бетонного элемента прямоугольной формы на действие изгибающего момента, нагрузка 180 т/см от нагрузки 900 кг/м как-то многовато даже для небоскреба из урана.
у меня получились другие цифры, плюс ошибка в разрядах. Не могу понять разницу между погонной нагрузкой и на м2 (см2), а также перевод в Н/М2 (Н/см2). При распределенной нагрузке 400 кг/м2 можно считать погонную 400 кг/м?

К сожалению, ни чем не могу вам помочь. Изгибающий момент действительно будет 180 т·см при нагрузке 900 кг/м и при пролете шарнирно опертой плиты l = 4 м.
Ваша формулировка «нагрузка 180 т/см от нагрузки 900 кг/м» мне не совсем понятна, думаю, вы просто ошиблись.
По поводу линейно распределенной нагрузки и нагрузки, распределенной на некоторой площади, смотрите статьи «Виды нагрузок или в чем сила, сопромат?» и «Определение нагрузки на конструкции в вопросах и ответах».

Док, спасибо за лекарство!При моем электронном образовании жизнь заставила лезть в дебри сопромата:) Еще вопрос: почему при расчете жб плиты, например 4х4, берете 1м её ширины? С условием, что расчетные данные можно применить к остальным метрам? Ведь даже по эпюрам видно, что нагрузки изменятся. И если взять для расчета 10 см плиты или полную длину, то результат меняется в десяток раз?
В литературе встретил: при расчете жб плиты 6х3,3 соотношение сторон 1,8 метра, шарнирно опертой,опирание по контуру,нагрузка рассчитывается при опирании по коротким сторонам,М=q*L1^2*L2/8.Как оцениваете рецепт?

Попробуем отделить мух от котлет. Если плита (4х4 м)имеет две опоры, то она может рассматриваться как балка, т.е. конструкция, испытывающая линейное напряженное состояние. Для такой плиты ширина принципиального значения не имеет. Расчет можно производить как для всей ширины плиты (например 4 м), так и для сколь угодно малого участка ширины (например 10 см). Но как правило расчеты в таких случаях производятся для 1 м ширины плиты, просто потому, что это упрощает расчеты. Да и для перевода нагрузки, приложенной к некоторой площади — плоской нагрузки — в линейную нагрузку никаких особенных математических действий не требуется: плоская нагрузка (кг/м^2) умножается на ширину рассматриваемого участка и если принятая ширина — 1 м, то и значение плоской нагрузки при переводе в линейную (кг/м) не изменяется.
Далее, если плита имеет опирание по контуру, то это уже плоское напряженное состояние. Такая плита представляет собой пластину, а расчет пластин — дело сложное и неблагодарное. На сегодняшний день методов точного расчета пластин не существует, впрочем существует несколько методов приближенного расчета. Один из них описан в статье «Расчет плиты опертой по контуру».
Ваш рецепт обсуждать здесь не буду.

Док, спасибо за ответ. Еще вопрос: чем отличаются расчеты в Ваших статьях «Расчет железобетонной плиты перекрытия, опертой по контуру» и «Расчет железобетонной плиты перекрытия»? Разные методики? Мне, как неспециалисту, тяжело въехать.

Так я вроде уж пояснил, в статье «Расчет железобетонной плиты перекрытия» рассматривается расчет плиты-балки по методике, сформулированной в действующем СНиПе. В статье «Расчет железобетонной плиты перекрытия, опертой по контуру» рассматривается расчет плиты-пластины. Методика в обоих случаях приблизительно одинаковая, разнится только подход к напряженному состоянию конструкции.

Здраствуйте Я хочу вычислат W сопротивлени момента для С-образный профили

Посмотрите статью «Расчет прочности потолочного профиля для гипсокартона», там как раз проводится расчет для С-образного профиля.

Уважаемый Доктор столкнулся с проблемой расчета стальных профилей с трапециевидными гофрами ГОСТ 24045-94. Суть в следующем: есть профиль Н114-600-0,8. Высота профиля 114 мм. Момент инерции поперечного сечения согласно ГОСТ 320,9 см в 4-й. Момент сопротивления min при сжатых узких полках(см. табл. ГОСТ) 53,3 см в 3-й. То есть Ymax (расстояние до центра тяжести сечения) равно 320,9/53,3 = 6,02 см.
Момент сопротивления max сжатых узких полках (см. табл. ГОСТ) 59,7 см в 3-й. Соответственно Ymin = 320,9/59,7 = 5,38 см. Таким образом получаем 6,02 + 5,38 =11,4 см (114 мм) то есть высота профиля. Аналогично проделаем эти же операции но при сжатых широких полках.
Момент инерции поперечного сечения 320,9 см в 4-й. Момент сопротивления min при сжатых широких полках(см. табл. ГОСТ) 52,4 см в 3-й. То есть Ymax (расстояние до центра тяжести сечения) равно 320,9/52,4 = 6,12 см.
Момент сопротивления max сжатых широких полках (см. табл. ГОСТ) 55,8 см в 3-й. Соответственно Ymin = 320,9/55,8 = 5,75 см. Таким образом получаем 6,12 + 5,75 = 11,9 см (119 мм) то есть больше высоты профиля. Как такое могло получиться?
Искренне буду вам признателен если поможете разобраться с это проблемой.

Я в составлении данного ГОСТа участия не принимал, потому могу только высказать свое личное мнение по этому поводу.
Дело в том, что при расчете сжимаемых элементов важна не только прочность, но и устойчивость. И чем больше длина элемента, тем сильнее это влияет на устойчивость. Соответственно, когда в зоне сжатия оказываются широкие полки, то значение момента сопротивления конечно же никоим образом не изменяется, однако, чтобы не возиться с дополнительными и довольно громоздкими расчетами, в ГОСТе дается значение момента сопротивления с учетом значения коэффициента продольного изгиба для данных элементов.

Доктор, уточните пожалуйста формулу 2.4. Сижу над курсовиком по ЖБК, обложился методичками, книжками и Интернетом, и начинаю дико ненавидеть сопромат за очепятки и недоговорки.

Данная статья предназначена для ознакомления с физическими основами расчета ЖБК, а не для выполнения расчетов. Современные методики расчета строятся на несколько иных допусках и предположениях и в них больше эмпирических формул.
Тем не менее физический смысл указанной вами формулы следующий: момент сопротивления арматуры относительно нейтральной оси сечения элемента равен собственно моменту сопротивления арматуры (которым из-за малого значения можно пренебречь) и произведения площади арматуры на расстояние от центра тяжести арматуры до нейтральной оси сечения, обозначенного литерой «у». А из приведенных выше формул следует, что этот момент сопротивления также равен произведению изгибающего момента на расчетное сопротивление стали.

hello!,I like your writing very a lot! proportion we keep in touch more approximately your article on AOL? I require a specialist on this area to unravel my problem. May be that’s you! Looking forward to look you. fdeddbcdaeeeeefe

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Строительный клуб

b — ширина сечения в мм; h — высота сечения в мм; y, z — центральные оси сечения.

Введите ширину сечения b в мм:

Введите высоту сечения h в мм:

В результате момент сопротивления W_y относительно центральной оси y равен:

В результате момент сопротивления W_z относительно центральной оси z равен:

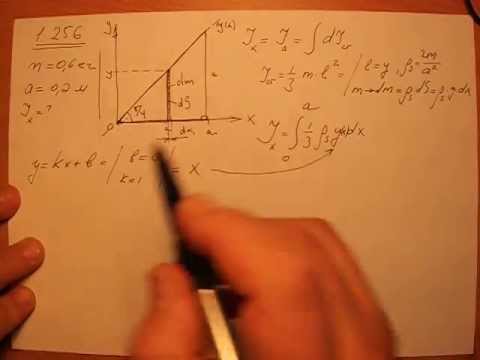
Как найти момент сопротивления прямоугольного сечения относительно его центральных осей?

Момент сопротивления сечения относительно осей z и y можно рассчитать по формулам:

W_y = b . h 2 /6,

W_z = h . b 2 /6,

W_y — момент сопротивления относительно центральной оси y в мм 3 ;

W_z — момент сопротивления относительно центральной оси z в мм 3 ;

b — ширина сечения в мм (см. на рисунке вверху статьи);

h — высота сечения в мм (см. на рисунке вверху статьи).

Момент сопротивления прямоугольного сечения

Онлайн-калькулятор позволит вычислить момент сопротивления прямоугольного сечения прилагая минимум усилий. Достаточно заполнить высоту и ширину искомого прямоугольника и вы тут же получите результат и расписанное решение.

Формула для определения осевого момента сопротивления прямоугольника

Для начала выясним что вообще обозначает эта величина.

Осевой момент сопротивления — это такая геометрическая характеристика сечения, которая выражается в виде отношения момента инерции к расстоянию до наиболее удаленной точки этого же сечения.

Формула для определения осевого момента сопротивления прямоугольного сечения выглядит так:

W_x = b * h 2 / 6 — момент сопротивления прямоугольника относительно оси X,

W_y = h * b 2 / 6 — момент сопротивления прямоугольника относительно оси Y, где

b — ширина прямоугольника,
h — высота прямоугольника.

Моменты сопротивления используются в инженерных расчетах на прочность и изгиб. Данный онлайн расчет пригодится студентам и инженерам-строителям.

💥 Видео