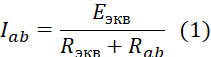Метод эквивалентного генератора треугольника (8 видео)

Метод эквивалентного генератора

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.

Алгоритм состоит из следующих шагов:

Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
Рассчитывается эквивалентная эдс генератора.
Определяется эквивалентное сопротивление генератора.
По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.

Содержание

Метод эквивалентного генератора: примеры решения
№9 Метод эквивалентного генератора.
Метод эквивалентного генератора треугольника
🔥 Видео

Метод эквивалентного генератора: примеры решения

Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).

Рис. 1. Метод эквивалентного генератора

Допустим, что необходимо рассчитать ток I_ab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.

Рис. 2. Эквивалентная электрическая схема

После преобразования ток через резистор R_ab (R4) определяется по формуле

Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).

Рис. 3. Режим холостого хода генератора

Для представленной схемы напряжение Еэкв будет равно

Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).

Рис. 4. Схема без источника эдс

Эквивалентное сопротивление полученной схемы определяется по формуле

Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).

Видео:Метод эквивалентного генератора МЭГ - Самое подробное объяснение задачиСкачать

№9 Метод эквивалентного генератора.

Этот метод основан на сформулированной выше теореме (См. предыдущую лекцию) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.

Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.

ЭДС ЕЭ эквивалентного генератора и его внутреннее сопротивление RЭ находятся из режимов холостого хода и короткого замыкания двухполюсника.

Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.

Пример 1.5. В цепи, показанной на рис. 9.1, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).

Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.

Рис. 9.1 — Схема решения задачи

а) Расчет режима холостого хода.

Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 9.2, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:

б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 9.2, б). Ток короткого замыкания: Ik=E1/R1=75 (A)

Внутреннее сопротивление эквивалентного генератора: Rэ=Ux/Ik=2 (Oм).

Рис. 9.2 — Режимы холостого хода (а) и короткого замыкания (б)

Величину Rэ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:

Ток в полученной неразветвленной цепи (рис. 9.1, б) определяется по закону Ома:

Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 9.3).

Рис. 9.3 — Зависимость тока от сопротивления

Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя Еэ и Rэ, а многократно используем лишь одну простую формулу (1.13).

Видео:Электротехника (ТОЭ). Лекция 9. Метод эквивалентного генератора | Решение задачСкачать

Метод эквивалентного генератора треугольника

Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.

Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Ход доказательства теоремы иллюстрируют схемы на рис. 1.

Пусть в схеме выделена некоторая ветвь с сопротивлением Z, а вся оставшаяся цепь обозначена как активный двухполюсник А (рис. 1,а). Разомкнем эту ветвь между точками 1 и 2 (рис. 1,б). На зажимах этой ветви имеет место напряжение . Если теперь между зажимами 1 и 2 включить источник ЭДС с направлением, указанным на рис. 1,в , то, как и в цепи на рис.1,б ток в ней будет равен нулю. Чтобы схему на рис. 1,в сделать эквивалентной цепи на рис. 1,а, в рассматриваемую ветвь нужно включить еще один источник ЭДС , компенсирующий действие первого (рис. 1,г). Будем теперь искать ток по принципу наложения, т.е. как сумму двух составляющих, одна из которых вызывается источниками, входящими в структуру активного двухполюсника, и источником ЭДС , расположенным между зажимами 1 и 2 слева, а другая – источником ЭДС , расположенным между зажимами 1 и 2 справа. Но первая из этих составляющих в соответствии с рис. 1,в равна нулю, а значит, ток определяется второй составляющей, т.е. по схеме на рис. 1,д, в которой активный двухполюсник А заменен пассивным двухполюсником П. Таким образом, теорема доказана.

Указанные в теореме ЭДС и сопротивление можно интерпретировать как соответствующие параметры некоторого эквивалентного исходному активному двухполюснику генератора, откуда и произошло название этого метода.

Таким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б.

Отсюда ток находится, как:

Метод эквивалентного генератора треугольника

(1)

где — напряжение на разомкнутых зажимах a-b.

Уравнение (1) представляет собой аналитическое выражение метода эквивалентного генератора.

Параметры эквивалентного генератора (активного двухполюсника) могут быть определены экспериментальным или теоретическим путями.

В первом случае, в частности на постоянном токе, в режиме холостого хода активного двухполюсника замеряют напряжение на его зажимах с помощью вольтметра, которое и равно . Затем закорачивают зажимы a и b активного двухполюсника с помощью амперметра, который показывает ток (см. рис. 2,б). Тогда на основании результатов измерений .

В принципе аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо определить комплексные значения и .

При теоретическом определении параметров эквивалентного генератора их расчет осуществляется в два этапа:

1. Любым из известных методов расчета линейных электрических цепей определяют напряжение на зажимах a-b активного двухполюсника при разомкнутой исследуемой ветви.

2. При разомкнутой исследуемой ветви определяется входное сопротивление активного двухполюсника, заменяемого при этом пассивным. Данная замена осуществляется путем устранения из структуры активного двухполюсника всех источников энергии, но при сохранении на их месте их собственных (внутренних) сопротивлений. В случае идеальных источников это соответствует закорачиванию всех источников ЭДС и размыканию всех ветвей с источниками тока.

Сказанное иллюстрируют схемы на рис. 3, где для расчета входного (эквивалентного) сопротивления активного двухполюсника на рис. 3,а последний преобразован в пассивный двухполюсник со структурой на рис. 3,б. Тогда согласно схеме на рис. 3,б

В качестве примера использования метода эквивалентного генератора для анализа определим зависимость показаний амперметра в схеме на рис. 4 при изменении сопротивления R переменного резистора в диагонали моста в пределах . Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60 Ом.

В соответствии с изложенной выше методикой определения параметров активного двухполюсника для нахождения значения перейдем к схеме на рис. 5, где напряжение на разомкнутых зажимах 1 и 2 определяет искомую ЭДС . В данной цепи

Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рис. 6.

Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно:

Таким образом, для показания амперметра в схеме на рис. 4 в соответствии с (1) можно записать

(2)

Задаваясь значениями R в пределах его изменения, на основании (2) получаем кривую на рис.7.

В качестве примера использования метода эквивалентного генератора для анализа цепи при синусоидальном питании определим, при каком значении нагрузочного сопротивления в цепи на рис. 8 в нем будет выделяться максимальная мощность, и чему она будет равна.

Параметры цепи: ; .

В соответствии с теоремой об активном двухполюснике обведенная пунктиром на рис. 8 часть схемы заменяется эквивалентным генератором с параметрами

В соответствии с (1) для тока через можно записать

откуда для модуля этого тока имеем

(3)

Анализ полученного выражения (3) показывает, что ток I, а следовательно, и мощность будут максимальны, если ; откуда , причем знак “-” показывает, что нагрузка имеет емкостный характер.

и .

Данные соотношения аналогичны соответствующим выражениям в цепи постоянного тока, для которой, как известно, максимальная мощность на нагрузке выделяется в режиме согласованной нагрузки, условие которого .

Таким образом, искомые значения и максимальной мощности: .

Теорема вариаций применяется в тех случаях, когда требуется рассчитать, насколько изменятся токи или напряжения в ветвях схемы, если в одной из ветвей этой схемы изменилось сопротивление.

Выделим на рис. 9,а некоторые ветви с токами и , а остальную часть схемы обозначим активным четырехполюсником А. При этом, полагаем что проводимости и известны.

Пусть сопротивление n-й ветви изменилось на . В результате этого токи в ветвях схемы будут соответственно равны и (рис. 9,б). На основании принципа компенсации заменим источником с ЭДС . Тогда в соответствии с принципом наложения можно считать, что приращения токов и вызваны в схеме на рис. 9,в, в которой активный четырехполюсник А заменен на пассивный П.

Для этой цепи можно записать

и .

Полученные соотношения позволяют определить изменения токов в m-й и n-й ветвях, вызванные изменением сопротивления в n-й ветви.

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

В каких случаях эффективно применение метода эквивалентного генератора?
Как можно экспериментально определить параметры эквивалентного генератора?
Как можно определить параметры активного двухполюсника расчетным путем?
Как необходимо преобразовать исходную схему активного двухполюсника для расчета его входного сопротивления?
В каких задачах используется теорема вариаций?
В цепи на рис. 4 источник ЭДС Е замене на источник тока J=10 А. Определить показание амперметра, если R=0.

Ответ: .

Для полученного значения в цепи на рис. 8 методом эквивалентного генератора определить ток в ветви с этим сопротивлением, если катушка индуктивности в структуре активного двухполюсника заменена на конденсатор с сопротивлением .