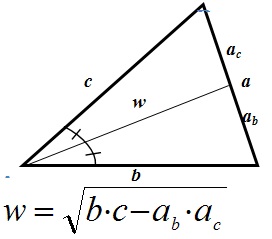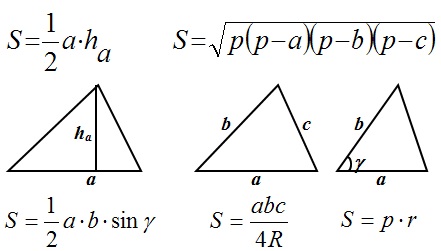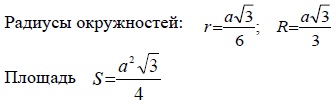Подготовка к ОГЭ по теме: «Треугольники»
Составители: учителя математики МОУ «Рамешковская СОШ» , .
Пояснительная записка: геометрическая часть экзаменационного теста чаще всего вызывает затруднение. Это происходит потому что геометрические задачи требуют иного подхода, чем любые другие. Тут необходимо применить нестандартное мышление и пространственное воображение, кроме того необходимо очень хорошо знать теоретический материал. Решение каждой задачи опирается на какое-либо правило, теорему или определение. Поэтому прежде всего нужно выучить теорию. В данном материале подобраны теория и задачи к ней.
Цель: 1. Систематизация знаний и способов деятельности обучающихся по математике по данному разделу за курс основной школы;
2. Подготовка обучающихся 9 класса к ОГЭ;
3. Успешное сдача ОГЭ.
Задачи: 1. Осуществить информационное, методическое обеспечение итоговой аттестации выпускников 9 классов;
2. Формирование «базы знаний» по геометрии, позволяющей беспрепятственно оперировать математическим материалом;
3. Формирование навыков определения типа задачи и оптимального способа ее решения;
4. Умение работать с геометрическими задачами.
Выбрать верные утверждения:
а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
б) Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны.
в)Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Два острых угла прямоугольного треугольника относятся как 11:79. Найдите больший острый угол. Ответ дайте в градусах. Один из острых углов прямоугольного треугольника равен 26◦. Найдите другой острый угол. Ответ дайте в градусах. Два острых угла прямоугольного треугольника относятся как 2:8. Найдите меньший острый угол. Ответ дайте в градусах. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.
В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 23◦. Найдите его другой острый угол. Ответ дайте в градусах. В треугольнике два угла равны 27◦ и 79◦. Найдите его третий угол. Ответ дайте в градусах. В треугольнике ABC известно, что AB=BC, ∠ABC = 146◦. Найдите ∠BCA. Ответ дайте в градусах. Какие из следующих утверждений верны:
а) Если угол острый, то смежный с ним угол также является острым.
б) Всегда один из двух смежных углов острый, а другой тупой.
в) Сумма углов треугольника равна 180◦.
г) Треугольника со сторонами 1, 2, 4 не существует.
д) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.
е) Сумма острых углов прямоугольного треугольника равна 90◦ .
ж) Смежные углы равны.
з) Один из углов треугольника всегда не превышает 60 градусов.
и) Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольник равны.
к) В тупоугольном треугольнике все углы тупые.
4. В треугольнике АВС стороны АС и ВС равны. Внешний угол при вершине В равен 116°. Найдите угол С. Ответ дайте в градусах.
Точка D на стороне АВ треугольника АВС выбрана так, что АD=АС. Известно, что ∠CАВ = 25◦. И ∠АСВ = 146◦. . Найдите ∠DCB. Ответ дайте в градусах.
В треугольнике АВС известно, что АС=ВС. Внешний угол при вершине В равен 107◦. Найдите угол С. Ответ дайте в градусах.
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите ∠МРN.
В треугольнике ABC известно, что ∠BCA= 60◦, AD биссектриса. Найдите ∠BAD. Ответ дайте в градусах. В треугольнике ABC известно, что AC= 58, BM-медианна, BM=37. Найдите AM. На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённую из вершины прямого угла.
В равностороннем треугольнике ABС биссектрисы СN и AM пересекаются в точке P. Найдите ∠МРN.
В треугольнике АВС известно, что АВ=ВС=25, АС=40. Найдите длину медианы ВМ. В треугольнике со сторонами 12 и 3 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 1. Чему равна высота, проведенная ко второй стороне?
Медиана ВМ и биссектриса АР треугольника АВС пересекаются в точке К, длина стороны АС относится к длине стороны АВ как 9:4. Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ. В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК:КМ=2:11. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника ВКР и площади треугольника АКМ. Медиана ВМ и биссектриса АР треугольника АВС пересекаются в точке К, длина стороны АС относится к длине стороны АВ как 11:6. Найдите отношение площади треугольника ВКР к площади треугольника АВК. Прямая параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите АС, если ВК:КА=2:3, КМ=4. Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Два катета прямоугольного треугольника равны 3 и 22. Найдите его площадь. Медиана равностороннего треугольника равна 12√3. Найдите его сторону. Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника. Стороны треугольника равны 12, 14 и 10. Найдите го площадь. Сторона треугольника равна 24, а высота, проведенная к этой стороне равна 19. Найдите площадь этого треугольника. В прямоугольном треугольнике катет и гипотенуза равны соответственно 12 и 20. Найдите другой катет этого треугольника. Бокова сторона равнобедренного треугольника равна 10, основание 12. Найдите его площадь. Найдите площадь равностороннего треугольника если его сторона равна 8. Стороны треугольна равны 10 и 6, угол между ними 30◦. Найдите его площадь. Сторона равностороннего треугольника равна 12√3. Найдите его биссектрису. В прямоугольном треугольнике меньший катет равен 6, а один из углов 30◦. Найдите площадь треугольника. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18. Стороны треугольника равны 16 и 9, угол между ними 60◦. Найдите его площадь. Высота треугольника, проведенная к гипотенузе делит ее на отрезки, равны 4 и 9. Найдите площадь треугольника. Гипотенуза равнобедренного треугольника равна 16. Найдите го площадь. Площадь треугольника равна 270 , сторона 5. Найдите высоту, проведенную к данной стороне. Один из катетов равен 12, другой составляет 0,6 первого. Найдите площадь этого треугольника. Гипотенуза треугольника равна 5, один из катетов равен 3. Найдите площадь этого треугольника. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√2. Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 36, а площадь равна 162√3. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Соотношения между сторонами и углами прямоугольного треугольника
В треугольнике ABC угол С равен 90◦, АС=4, cosA=0,5. Найдите АВ.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
В прямоугольном треугольнике ∠С=90◦, tgА=3,5. Найти АС, если ВС=2,8. В равнобедренном треугольнике АВС ВС=СА=15. Чему равна высота, опущенная на АВ, если sinA=0,9. Найдите tgA треугольника ABC, изображенного на рисунке.
Катеты прямоугольного треугольника равны √15 и 1. Найдите синус наименьшего угла этого треугольника.
В треугольнике АВС средняя линия MN параллельна стороне AC. Найдите периметр треугольника ABC, если периметр треугольника MBN равен 17 см. В треугольнике АВС DE – средняя линия. Площадь треугольника CDE равна 20. Найдите площадь треугольника АВС.
Периметр равностороннего треугольника АВС равен 24 см. Найдите длину средней линии этого треугольника. Точки M и N являются серединами сторон АВ и ВС треугольника АВС, АС=22. Найдите MN. Точки D и K являются серединами сторон АВ и ВС треугольника АВС, АС=88. Найдите DK. В треугольнике АВС известно, что DE – средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника АВС.
В треугольнике АВС отмечены середины М и N сторон ВС и АС соответственно. Площадь треугольника CNМ равна 38. Найдите площадь четырехугольника ABMN.
В треугольнике АВС АС = 35, ВС=5√15 угол С равен 90°. Найдите радиус описанной окружности этого треугольника. Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?
Сторона AC треугольника ABC содержит центр описанной около него окружности. Найдите ∠С, если ∠А=75◦. Ответ дайте в градусах.
В треугольнике АВС известны длины сторон АВ=48, АС=72, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD. Углы В и С треугольника АВС равны соответственно 71◦ и 79◦. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 8. В треугольнике АВС известно, что АС=15, ВС= 5√7, угол С равен 80◦. Найдите радиус описанной окружности этого треугольника. Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
- Комплект заданий для подготовки к ОГЭ по теме «Треугольники» (Часть 1) материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- Задание №16 ОГЭ по математике
- Треугольники, четырёхугольники, многоугольники и их элементы
- Теория к заданию №16
- Разбор типовых вариантов заданий №16 ОГЭ по математике
- Первый вариант задания
- Второй вариант задания
- Третий вариант задания
- Четвертый вариант задания
- Пятый вариант задания
- Шестой вариант задания
- Седьмой вариант задания
- Восьмой вариант задания
- Девятый вариант задания
- Десятый вариант задания
- Демонстрационный вариант ОГЭ 2019
- 🎬 Видео
Видео:Как находить медианы и высоты треугольника || ЕГЭ-2022 || ОГЭ - 2022Скачать

Комплект заданий для подготовки к ОГЭ по теме «Треугольники» (Часть 1)
материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему
В комплект входит файл с теорией, задания с кратким ответом, задания на распознавание ошибочных заключений, презентация к заданиям последнего вида.
Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| teoriya_dlya_pechati.doc | 408 КБ |
| zadachi_s_kratkim_otvetom.doc | 104 КБ |
| vernye_nevernye.doc | 53 КБ |
| vernye_i_nevernye.pptx | 184.96 КБ |
Видео:Медиана в ОГЭ #огэ #огэматематика #математикаСкачать

Предварительный просмотр:
Признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников
1. По двум катетам
3. По катету и острому углу
2. По катету и гипотенузе
4. По гипотенузе и острому углу
Теорема о сумме углов треугольника и следствия из неё.
1. Сумма внутренних углов треугольника равна .
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3. Внешний угол треугольника больше любого угла треугольника, не смежного с ним
Неравенство треугольника. Следствия из неравенства треугольника
1. Сумма двух сторон треугольника больше третьей стороны.
2. Против большего угла треугольника лежит большая сторона.
3. Против большей стороны треугольника лежит больший угол.
4. Гипотенуза прямоугольного треугольника больше катета.
Основные свойства и признаки равнобедренного треугольника.
Треугольник называется равнобедренным , если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием.
1. В равнобедренном треугольнике углы при основании равны.
2. Если в треугольнике два угла равны, то он равнобедренный.
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
4. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
Средняя линия треугольника.
Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
Теоремы о медианах треугольника.
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Свойство биссектрисы треугольника.
Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Квадрат биссектрисы треугольника равен произведению сторон, её заключающих, без произведения отрезков третьей стороны, на которые она разделена биссектрисой.
1. Теорема Пифагора . Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Теорема, обратная теореме Пифагора. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
3. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
4. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла.
5. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы.
6. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 0 .
7. ; , где — катеты, — гипотенуза, и — радиусы соответственно вписанной и описанной окружности.
8. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу,
9. Катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике.
1. Теорема косинусов . Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
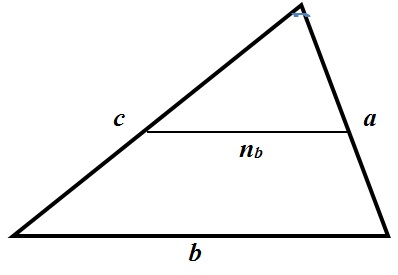
2. Формула для медианы треугольника . Если mс — медиана треугольника, проведенная к стороне c , то , где a и b — остальные стороны треугольника.
3. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
,
где R – радиус, описанной около треугольника окружности
4. Обобщенная теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника.
1. Площадь треугольника равна половине произведения основания на высоту.
2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
4. Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности.
3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
5. Формула Герона.
Элементы равностороннего треугольника.
Пусть h ,S, r, R — высота, площадь, радиусы описанной и вписанной окружности равностороннего треугольника со стороной a .
1. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
2. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны.
Отношение соответствующих линейных элементов подобных треугольников равно коэффициенту подобия.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Видео:как я сдавала огэ+реакция на результаты|физика&информатикаСкачать

Предварительный просмотр:
Задачи с кратким ответом
Вычисление углов и длин
В треугольнике АВС угол А равен , внешний угол при вершине В равен . Найдите градусную меру угла С .
В треугольнике АВС угол С равен , АС = ВС. Найдите градусную меру внешнего угла при вершине В .
Градусные меры углов треугольника относятся как
2 : 3 : 7. Найдите градусную меру меньшего из углов треугольника.
В треугольнике АВС угол С равен , АD – биссектриса угла А, угол ВAD равен . Найдите градусную меру угла ВDA .
В прямоугольном треугольнике один из острых углов в 5 раз больше другого. Найдите градусную меру большего острого угла данного треугольника.
Мальчик прошел от дома по направлению на запад 120 м. Затем повернул на север и прошел 50 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Группа туристов двигалась от станции на север 2ч со скоростью 4 км/ч, а затем на восток 3ч со скоростью 2 км/ч. На каком расстоянии (в километрах) от станции оказалась группа туристов?
На какой высоте будет находиться верхний конец лестницы, длиной 13 м, если нижний её конец находится на расстоянии 5 м от стены.
Два острых угла прямоугольного треугольника относятся как 11:34. Найдите больший острый угол. Ответ дайте в градусах.
Острые углы прямоугольного треугольника равны 29º и 61º. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла.
По данным рисунка найдите площадь треугольника.
По данным рисунка найдите площадь треугольника.
По данным рисунка найдите площадь треугольника.
По данным рисунка найдите площадь треугольника.
В треугольнике АВС проведена высота СН. Известно, что АВ = 3СН, СН = 3. Найдите площадь треугольника.
В прямоугольном треугольнике один из катетов равен 6, а угол, лежащий напротив него, равен . Найдите площадь треугольника.
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен . Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен . Найдите площадь треугольника.
Периметр треугольника равен 24 см, а радиус вписанной в него окружности — 3 см. Найдите площадь треугольника.
Видео:25 задание ОГЭ ✧ В ∆ABC биссектриса BE и медиана AD перпендикулярны и ... #огэ #егэ #геометрияСкачать
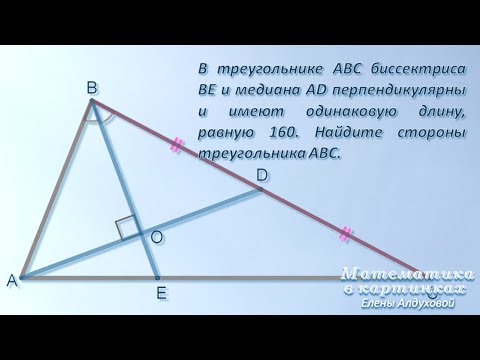
Предварительный просмотр:
Какие из следующих утверждений верны?
- Если медиана и высота, проведенные из одной вершины треугольника, не совпадают, то этот треугольник не является равнобедренным.
- Если биссектриса треугольника делит противоположную сторону на равные отрезки, то этот треугольник равнобедренный.
- Если треугольник равносторонний, то длина любой его высоты равна длине любой его биссектрисы.
- Если треугольник равнобедренный, то наименьшей из сторон является его основание.
- Каждая сторона треугольника меньше разности двух других сторон.
- В равнобедренном треугольнике имеется не более двух равных углов.
- Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
- В треугольнике АВС, для которого АВ = 3, ВС = 4, АС = 5 угол наименьший.
- В треугольнике против меньшего угла лежит большая сторона.
- Если один угол треугольника больше 120 0 , то оба других его угла меньше 30 0 .
- Если все стороны треугольника меньше 1, то и все его высоты меньше 1.
- Сумма острых углов прямоугольного треугольника не превосходит .
- В треугольнике , для которого , , , сторона — наименьшая.
- В треугольнике , для которого ,
, , угол — наибольший.
- Внешний угол треугольника больше каждого внутреннего угла.
- Треугольник со сторонами 1, 2, 3 не существует.
- Около всякого треугольника можно описать не более одной окружности.
- В любой треугольник можно вписать не менее одной окружности.
- Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
- Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Выберите неверные утверждения
- Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.
- Любые два равнобедренных треугольника подобны.
- Любые два прямоугольных треугольника подобны.
- Треугольник ABC , у которого , , , является тупоугольным.
- Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.
- Любые два равносторонних треугольника подобны.
- Треугольник ABC , у которого ,
, , является прямоугольным.
- В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов катетов.
- Стороны треугольника пропорциональны синусам прилежащих углов.
- Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны.
- Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними.
- Любые два прямоугольных и равнобедренных треугольника подобны.
- Если в треугольнике два угла равны, то он равнобедренный.
- В равнобедренном треугольнике отрезок, соединяющий любую точку основания, отличную от вершины, с противоположной вершиной, меньше боковой стороны.
- В треугольнике против меньшей стороны лежит больший угол.
- Если в треугольнике два угла по 70°, то он тупоугольный.
- Каждая сторона треугольника меньше суммы двух других сторон.
- Существует треугольник со сторонами 2, 4, 7.
- Площадь треугольника меньше произведения двух его сторон.
- Площадь треугольника равна произведению его периметра на радиус вписанной окружности.
Предварительный просмотр:
Видео:Геометрия Задача многоходовка про медиану и биссектрису № 26 ОГЭ 2020Скачать

Подписи к слайдам:
1.Какие из следующих утверждений верны ? 1) Если медиана и высота, проведенные из одной вершины треугольника, не совпадают, то этот треугольник не является равнобедренным. 2) Если биссектриса треугольника делит противоположную сторону на равные отрезки, то этот треугольник равнобедренный. 3) Если треугольник равносторонний, то длина любой его высоты равна длине любой его биссектрисы . 4) Если треугольник равнобедренный, то наименьшей из сторон является его основание . 05.10.2012 2
2.Какие из следующих утверждений верны? 1) Каждая сторона треугольника меньше разности двух других сторон. 2) В равнобедренном треугольнике медиана является биссектрисой и высотой. 3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны. 4) В треугольнике АВС, для которого АВ = 3, ВС = 4, АС = 5 угол С наименьший. 05.10.2012 3
3. Какие из следующих утверждений верны? 1) В треугольнике против меньшего угла лежит большая сторона. 2) Если один угол треугольника больше 120 0 , то оба других его угла меньше 30 0 . 3) Если все стороны треугольника меньше 1, то и все его высоты меньше 1. 4) Сумма острых углов прямоугольного треугольника не превосходит 90 0 . 05.10.2012 4
4.Какие из следующих утверждений верны? 1) В треугольнике , для которого , , , сторона ВС — наименьшая. 2) В треугольнике, для которого АВ = 4, ВС =5, АС= 6, угол В — наибольший. 3) Внешний угол треугольника больше каждого внутреннего угла. 4) Треугольник со сторонами 1, 2, 3 не существует. 05.10.2012 5
5.Какие из следующих утверждений верны? 1) Около всякого треугольника можно описать не более одной окружности. 2) В любой треугольник можно вписать не более одной окружности. 3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис. 4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам. 05.10.2012 6
6. Выберите неверные утверждения 1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. 2) Любые два равнобедренных треугольника подобны. 3) Любые два прямоугольных треугольника подобны. 4) Треугольник ABC , у которого АВ = 3, ВС = 4, АС = 5 , является тупоугольным. 05.10.2012 7
7. Выберите неверные утверждения 1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними. 2) Любые два равносторонних треугольника подобны. 3) Треугольник ABC , у которого АВ = 4, ВС=5, АС = 6, является прямоугольным. 4) В прямоугольном треугольнике квадрат гипотенузы не превосходит суммы квадратов катетов. 05.10.2012 8
8. Выберите неверные утверждения 1) Стороны треугольника пропорциональны синусам противолежащих углов. 2) Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны. 3) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними. 4) Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. 05.10.2012 9
9 . Выберите неверные утверждения 1) Если в треугольнике два угла равны, то он равнобедренный. 2) В равнобедренном треугольнике отрезок, соединяющий любую точку основания, отличную от вершины, с противоположной вершиной, меньше боковой стороны. 3) В треугольнике против меньшей стороны лежит больший угол. 4) Если в треугольнике два угла по 70°, то он тупоугольный. 05.10.2012 10
10 . Выберите неверные утверждения 1) Каждая сторона треугольника меньше суммы двух других сторон. 2) Существует треугольник со сторонами 2, 4, 7. 3) Площадь треугольника меньше произведения двух его сторон. 4) Площадь треугольника равна произведению его периметра на радиус вписанной окружности. 05.10.2012 11
Видео:Вся геометрия 7–9 класс с нуля | ОГЭ МАТЕМАТИКА 2023Скачать

Задание №16 ОГЭ по математике
Видео:Все типы 15 задания ОГЭ 2022 математика | Геометрия на ОГЭСкачать

Треугольники, четырёхугольники, многоугольники и их элементы
Перейдем к разбору модуля «Геометрия». В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №16
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
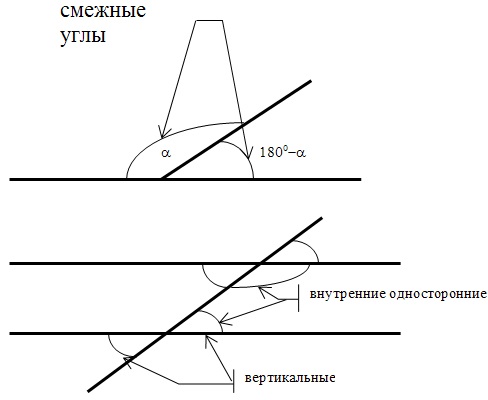
Вначале предлагаю рассмотреть углы на плоскости:
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
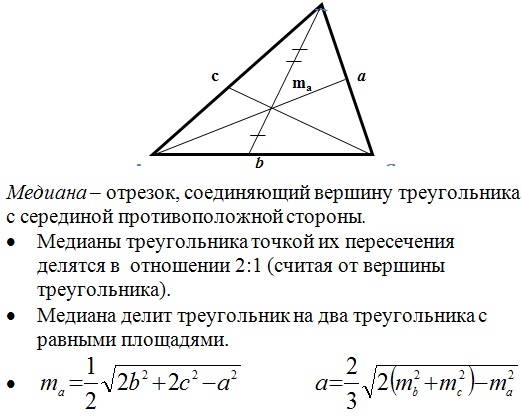
Медиана:
Теперь вспомним основные формулы нахождения площади треугольника:
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
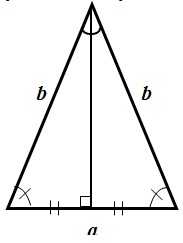
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник — треугольник, у которого две стороны равны.
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
Прямоугольный треугольник:
Разбор типовых вариантов заданий №16 ОГЭ по математике
Первый вариант задания
В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Второй вариант задания
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Решение:
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Третий вариант задания
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Решение:
Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
Так как углы при основании равны, значит угол BCA равен углу BAC:
58° = ∠BCA + ∠BAC = 2 ∠BCA
Четвертый вариант задания
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Решение:
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Пятый вариант задания
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Решение:
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
Шестой вариант задания
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Решение:
Для решения необходимо вспомнить определение медианы.
Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Седьмой вариант задания
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение:
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
Восьмой вариант задания
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Решение:
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Девятый вариант задания
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Решение:
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
Десятый вариант задания
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
Решение:
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
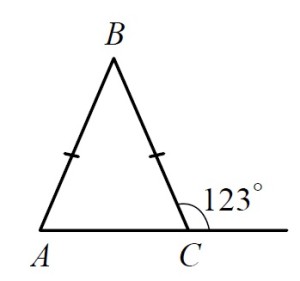
Демонстрационный вариант ОГЭ 2019
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
Решение:
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
🎬 Видео
Шины ОГЭ 2023. Задания 1-5 ОГЭ по математикеСкачать

Разбор ОГЭ по информатике на 5 за 25 минутСкачать

Медиана прямоугольного треугольника— Геометрия ОГЭСкачать
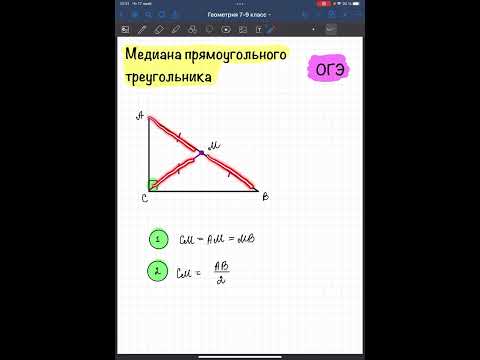
Высота, биссектриса, медиана. 7 класс.Скачать

Геометрия Задача № 25 ОГЭ 2021Скачать

ОГЭ Задание 24 Свойство медиан треугольникаСкачать

Задание 16 ОГЭ 2022 математика | Точка пересечения медиан треугольникаСкачать

8. Медиана треугольника и её свойства.Скачать

Медиана в прямоугольном треугольнике на ЕГЭ и ОГЭ по профильной математикеСкачать

Задача за секунду. ОГЭ геметрия. Медиана прямоугольного треугольникаСкачать
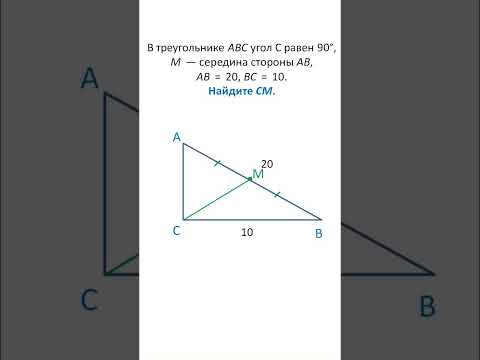
15 задание ОГЭ 2023 Медиана треугольника Short #shortsСкачать

Задание 25 из реального ОГЭ по математике 2023 | УмскулСкачать