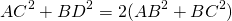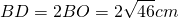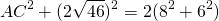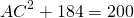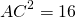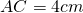Медиана треугольника как найти сторону

Знание — сила. Познавательная информация

Видео:Длина медианы треугольникаСкачать

По сторонам и медиане найти сторону треугольника

Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.

По двум сторонам и медиане найти третью сторону треугольника — задача, обратная нахождению медианы треугольника по трем его сторонам .

Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.

Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.

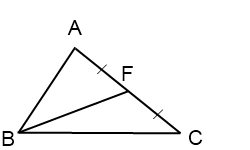
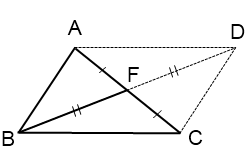
На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.

Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.

Переходим к решению конкретной задачи.

По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.

Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.

Видео:Задача найти сторону равностороннего треугольника по медианеСкачать

Найти сторону треугольника через медиану и стороны

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

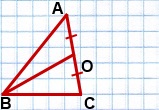
BO — медиана, BO=√46 см.

1) На луче BO отложим отрезок OD,

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Определение и свойства медианы равностороннего треугольника

В данной статье мы рассмотрим определение и свойства медианы равностороннего треугольника, а также разберем примеры решения задач для закрепления изложенного материала.

Видео:Уравнения стороны треугольника и медианыСкачать

Определение медианы

Медиана – это отрезок, соединяющий вершину треугольника и середину противоположной стороны.

Треугольник называется равносторонним, если все его стороны равны (AB = BC = AC).

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

Свойства медианы равностороннего треугольника

Свойство 1

Любая медиана в равностороннем треугольнике одновременно является и высотой, и серединным перпендикуляром, и биссектрисой угла, из которого проведена.

BD – медиана, высота и серединный перпендикуляр к стороне AC, а также биссектриса угла ABC;

Свойство 2

Все три медианы в равностороннем треугольнике равны между собой. Т.е. AF = BD = CE.

Свойство 3

Медианы в равностороннем треугольнике пресекаются в одной точке, которая делит их в отношении 2:1.

Свойство 4

Любая медиана равностороннего треугольника делит его на два равных по площади (равновеликих) прямоугольных треугольника. Т.е. S₁ = S₂.

Свойство 5

Равносторонний треугольник делится тремя медианами на шесть равновеликих прямоугольных треугольников. Т.е. S₁ = S₂ = S₃ = S₄ = S₅ = S₆.

Свойство 6

Точка пересечения медиан в равностороннем треугольнике является центром описанной вокруг и вписанной окружностей.

• r – радиус вписанной окружности;
• R – радиус описанной окружности;
• R = 2r (следует из Свойства 3).

Свойство 7

Длину медианы равностороннего треугольника можно вычислить по формуле:

a – сторона треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Примеры задач

Задача 1
Вычислите длину медианы равностороннего треугольника, если известно, что его сторона равна 6 см.

Решение
Для нахождения требуемого значения применим формулу выше:

Задача 2
Самая большая сторона одного из треугольников, образованных в результате пересечения трех медиан в равностороннем треугольнике, равняется 8 см. Найдите длину стороны данного треугольника.

Решение
Нарисуем чертеж согласно условиям задачи.

Из Свойства 5 мы знаем, что в результате пересечения всех медиан образуются 6 прямоугольных треугольников.

• BG = 8 см (самая большая сторона, является гипотенузой △BFG);
• FG = 4 см (катет △BFG, в 2 раза меньше гипотенузы BG – следует из Свойства 3).

Применяем теорему Пифагора, чтобы найти длину второго катета BF:
BF 2 = BG 2 – FG 2 = 8 2 – 4 2 = 48 см 2 .
Следовательно, BF ≈ 6,93 см.

BF равняется половине стороны BC (т.к. медиана делит сторону треугольника пополам), следовательно, BC ≈ 13,86 см.

🎬 Видео

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

8. Медиана треугольника и её свойства.Скачать

Как найти медиану треугольника по его сторонамСкачать

Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

Как найти медиану, зная стороны треугольника? Удвоение медианы.Скачать

№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

ЗАДАЧА ДЛЯ ОТЛИЧНИКОВ | Как найти медиану треугольника через стороныСкачать

Формулы для медианы треугольникаСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задание 9 ОГЭ от ФИПИСкачать

Построение медианы в треугольникеСкачать

Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Треугольник с перпендикулярными медианами. Как найти третью сторону по известным двум?Скачать