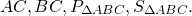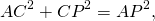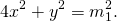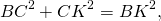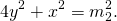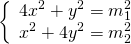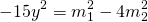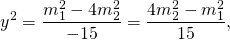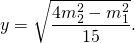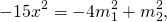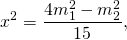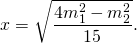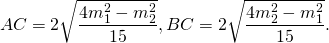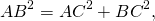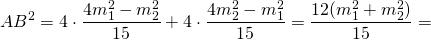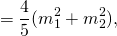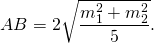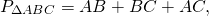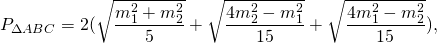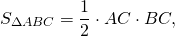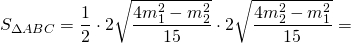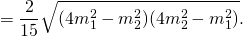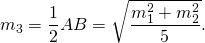В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.
Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Определение медианы прямоугольного треугольника
Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника
Свойство 1
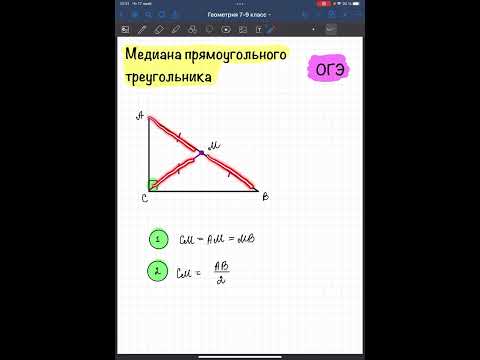
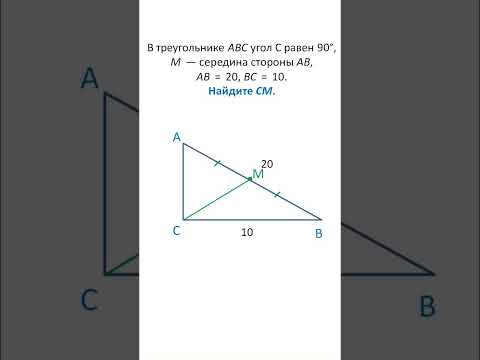
Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.
- BC = 2AD
- AD = BD = DC
Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.
Свойство 2
Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.
Для нашего треугольника (см. рисунок выше):
Это следует из теоремы Пифагора и Свойства 1.
Свойство 3
Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.
Т.е. BO – это одновременно и медиана, и радиус.
Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Пример задачи
Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.
Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.
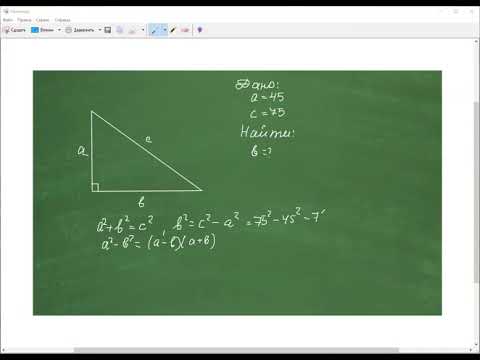
Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.
Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P△ = 12 см + 16 см + 20 см = 48 см.
Видео:Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Медианы, проведенные к катетам
Что можно сказать о прямоугольном треугольнике, в котором известны медианы, проведенные к катетам?
Медиана, проведённая к катету, разбивает исходный треугольник на два треугольника, один из которых также прямоугольный. Эти треугольники имеют равные площади.
В точке пересечения медианы делятся в отношении 2:1, считая от вершины. Если провести третью медиану, исходный треугольник разбивается на 6 равновеликих треугольников.
Из двух медиан больше та, которая проведена к наименьшей стороне. Таким образом, медиана, проведённая к гипотенузе — наименьшая.
По известным длинам проведённых к катетам медиан можно найти остальные стороны прямоугольного треугольника.
В прямоугольном треугольнике медианы, проведенные к катетам, равны m1 и m2. Найти катеты, периметр и площадь этого треугольника.
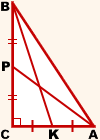
AP, CF — медианы, AP=m1, BK=m2
Для определенности, возьмём BC>AC, следовательно, m1
Аналогично, из треугольника BCK
Умножим второе уравнение системы на -4 и сложим с первым:
Аналогично, умножив первое уравнение на -4 и сложив со вторым, получаем
Из треугольника ABC по теореме Пифагора
Периметр треугольника ABC равен
Поскольку медиана, проведённая к гипотенузе, равна её половине, можно найти третью медиану как
Запоминать эти формулы не нужно, при решении конкретной задачи достаточно повторить эти рассуждения.
Видео:Медиана в прямоугольном треугольникеСкачать

Все формулы медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.
Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).
M — медиана
R — радиус описанной окружности
O — центр описанной окружности
с — гипотенуза
a, b — катеты
α — острый угол CAB
Медиана равна радиусу и половине гипотенузы, ( M ):
Формула длины через катеты, ( M ):
Формула длины через катет и острый угол, ( M ):
🎬 Видео
ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Медиана в прямоугольном треугольникеСкачать

8. Медиана треугольника и её свойства.Скачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Медиана прямоугольного треугольника— Геометрия ОГЭСкачать
Урок 22. Свойство катета прямоугольного треугольника, лежащего против угла в 30° (7 класс)Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Теорема Пифагора для чайников)))Скачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Лайфхак нахождения катета в прямоугольном треугольникеСкачать
Задача за секунду. ОГЭ геметрия. Медиана прямоугольного треугольникаСкачать
Катеты и гипотенузаСкачать

Свойство медианы в прямоугольном треугольнике. Практическая часть. 8 класс.Скачать