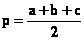Линейный алгоритм вычисления площади треугольника (7 видео)

Линейный алгоритм вычисления площади треугольника

6.2. ОСНОВНЫЕ ТИПЫ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ

Наиболее простым видом алгоритма является линейный алгоритм, при котором действия выполняются последовательно, одно за другим, без разветвлений и возвратов.

Пример . Вычисление площади треугольника по трем сторонам a , b , c по формуле Герона:

, где

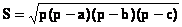
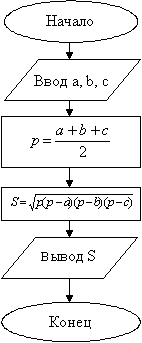
Блок-схема алгоритма имеет вид:

В процессе решения многих задач часто возникает необходимость в зависимости от исходных данных или получающихся промежуточных результатов проводить вычисления либо по одним, либо по другим формулам, т.е. по разным направлениям – ветвям. Такой вычислительный алгоритм называется разветвляющимся.

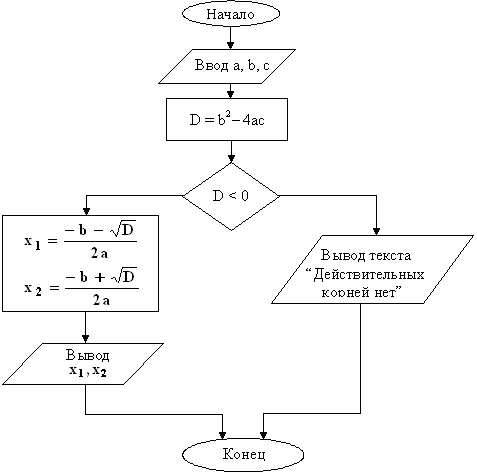
Пример. Нахождение действительных корней квадратного уравнения

Блок-схема алгоритма имеет вид:

При решении большинства практических задач возникает необходимость неоднократного повторения однотипных действий при различных значениях параметров, определяющих эти действия. Такие алгоритмы называются циклическими, а повторяемые участки вычислений – циклами.

Пример . Вычисление факториала натурального числа

Содержание

Линейный алгоритм вычисления площади треугольника
Линейный алгоритм в Паскале
При координатах: х1=10 у1=15 х2=15 у2=20 х3=25 у3=30
При координатах: х1=10 у1=15 х2=15 у2=20 х3=25 у3=30
Дистанционное обучение как современный формат преподавания
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
📹 Видео

Видео:Вычисление площади треугольника через основание и высоту в программе на языке ПаскальСкачать

Линейный алгоритм вычисления площади треугольника

3. Можно ли подобрать такое значение a, b,c, чтобы значение S содержало нули в дробной части?

Пример 3. Вычислите расстояние d между двумя точками с координатами х1,у1,х2,у2 (расстояние ).

Этапы выполнения задания.

I. Определение исходных данных: переменные х1,у1,х2,у2 (координаты двух точек).

II. Определение результатов: переменная d (расстояние между точками).

III. Алгоритм решения задачи.

1. Ввод исходных данных

2. Вычисление значения расстояния по формуле

3. Вывод результата.

IV. Описание переменных:

Все переменные, определенные для решения задачи, имеют тип real .

Write(‘введите координаты х1,у1,х2,у2:’);

d :=SQRT( sqr ( x1-x2)+sqr(y1-y2) );

Можешь загрузить! Пример 3

1. Запустите программу и введите значения

х1 =1 ,у1 =2 ,х2 =3 ,у2 =4

Проверьте, результат должен быть следующим:

Проверить правильность вычислений можно на калькуляторе.

2. Заполните таблицу

678

2.15.87.3

0.236-2.36-5.61

3. Можно ли подобрать такие значения х1,у1,х2,у2, чтобы значение d содержало нули в дробной части?

Проверка знаний Тест: Вычисление по формулам

Задачи для самостоятельного решения

Даны стороны a и b прямоугольника. Вычислите периметр, длину диагонали и площадь прямоугольника.

Формулы: р=2*( a+b), s=a*b ,

Дана сторона a равностороннего треугольника. Вычислите периметр и площадь треугольника.

Дана длина ребра куба a . Вычислите диагональ куба, объем куба и площадь его боковой поверхности.

Формулы: V =a 3 , S _бок=6*а 2 ,

Треугольник задан координатами своих вершин х1,у1,х2,у2,х3,у3. Вычислите площадь треугольника.

Задана температура в градусах по шкале Цельсия. Используя формулу перевода температуры из градусов по шкале Цельсия в градусы по шкале Фаренгейта F = 1.8 С + 32 получите температуру по Фаренгейту.

Видео:Найти площадь прямоугольника, треугольника или круга. Решение задачи на PythonСкачать

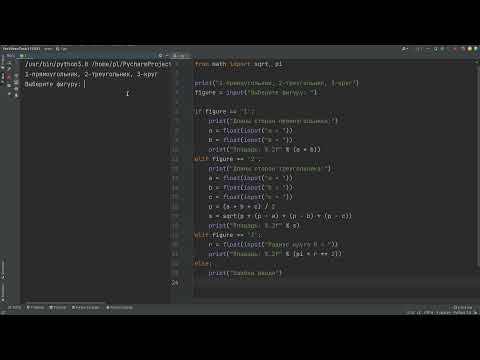
Линейный алгоритм в Паскале

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Лабораторная работа 1

По теме: «Программирование алгоритмов линейной структуры».

Цель : овладение практическими навыками разработки и программирования линейных вычислительных процессов и навыками по отладке и тестированию программ.

Задания для самостоятельной подготовки:

Запись констант, переменных, стандартных функций;

Правила записи арифметических выражений;

Организацию ввода/вывода данных.

Составьте алгоритм, программу и выполните её на ЭВМ. На печать выведите значения вводимых данных и результаты вычислений, сопровождая их наименованиями переменных и комментариями.

Модифицируйте программу так, чтобы ввод значений с клавиатуры осуществлялся в соответствии с подсказкой, значения каких переменных надо вводить.

Пример выполнения работы:

Пример 1. Треугольник задан координатами своих вершин Х1,У1,Х2,У2,Х3,У3.

Составьте программу вычисления площади треугольника по формуле Герона при х1=10;у1=15; х2=15;у2=20;х3=25;у3=30.

Х1,У1,Х2,У2,Х3,У3 – координаты вершин треугольника;

a, b, c – длины сторон треугольника;

p – полупериметр треугольника;

s – площадь треугольника.

s = √р*(р – а)*(р – b )*(р – с),

Так как значения Х1,У1,Х2,У2,Х3,У3 известны, то их можно ввести в раздел оконстант.

a, b, c, p, s – опишем в разделе переменных как real.

Алгоритм решения задачи:

c:= √(x3-x1) 2 + (y3-y1) 2 ;

Программа решение задачи будет иметь вид:

x1=10;y1=15; (* координаты первой вершины треугольника *)

x2=15; y2=20; (* координаты второй вершины треугольника *)

x3=25; y3=30; (* координаты третьей вершины треугольника *)

a, b, c: real ; (* длина сторон треугольника *)

p: real; (* полупериметр треугольника *)

s: real ; (* площадь треугольника *)

a:= sqrt(sqr(x2-x1)+sqr(y2-y1)); (* вычисление длины стороны треугольника а *)

b:= sqrt(sqr(x3-x2)+sqr(y3-y2)); (* вычисление длины стороны треугольника b *)

c:= sqrt(sqr(x3-x1)+sqr(y3-y1)); (* вычисление длины стороны треугольника c *)

p:= (a + b + c )/2; (* вычисление полупериметра треугольника *)

s : = sqrt(p*(р-а)*(р-b)*(p-c)); (* вычисление площади треугольника *)

write (‘ При координатах : x1=’,x1:2,’ ‘:3,’y1=’,y1:2,’ ‘:3,’x2=’,x2:2,’ ‘:3,’y2=’,y2:2,’ ‘:3,’x3=’,x3:2,’ ‘:3,’y3=’,y3:2);

writeln (‘ вычисление площади треугольника ’);

Первый оператор вывода WRITELN печатает текст на экране с первой позиции строки. Выводит значения координат по формату 2:0 через три пробела. Второй оператор выводит на экран текст и готовит вывод информации с новой строки. Третий оператор печатает обозначение сторон треугольника, полупериметра по формату 4:2, а площади – 6:3, выводит их значения на экран, отделяя их друг от друга тремя пробелами.

В результате на экране получим сообщение:

Видео:Уроки программирования на языке Pascal. Вычисление площади треугольника по координатам вершинСкачать

При координатах: х1=10 у1=15 х2=15 у2=20 х3=25 у3=30

Вычисление площади треугольника

x1,y1,x2,y2,x3,y3: real; (* координаты вершин треугольника *)

a, b, c: real ; (* длина сторон треугольника *)

p: real; (* полупериметр треугольника *)

s: real ; (* площадь треугольника *)

Writeln ( ‘ Введите координаты вершин треугольника ’);

Writeln (‘ x1=10,y1=15,x2=15,y2=20, x3=25,y3=30’);

a:= sqrt(sqr(x2-x1)+sqr(y2-y1)); (* вычисление длины стороны треугольника а *)

b:= sqrt(sqr(x3-x2)+sqr(y3-y2)); (* вычисление длины стороны треугольника b *)

c:= sqrt(sqr(x3-x1)+sqr(y3-y1)); (* вычисление длины стороны треугольника c *)

p:= (a + b + c )/2; (* вычисление полупериметра треугольника *)

s : = sqrt(p*(р-а)*(р-b)*(p-c)); (* вычисление площади треугольника *)

write (‘ При координатах : x1=’,x1:2,’ ‘:3,’y1=’,y1:2,’ ‘:3,’x2=’,x2:2,’ ‘:3,’y2=’,y2:2,’ ‘:3,’x3=’,x3:2,’ ‘:3,’y3=’,y3:2);

writeln (‘ вычисление площади треугольника ’);

В результате на экране получим сообщение:

Введите координаты вершин треугольника

Видео:Решение простых задач на python | Площадь и периметр прямоугольного треугольникаСкачать

При координатах: х1=10 у1=15 х2=15 у2=20 х3=25 у3=30

Вычисление площади треугольника

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Курс добавлен 23.11.2021
Сейчас обучается 49 человек из 30 регионов

Курс повышения квалификации

Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam

Курс добавлен 31.01.2022
Сейчас обучается 32 человека из 18 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Нахождение площади треугольника в С++Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 554 574 материала в базе

Другие материалы

10.05.2016
921
6

10.05.2016
28269
271

10.05.2016
609
0

10.05.2016
1090
1

10.05.2016
1422
1

10.05.2016
3152
18

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

10.05.2016 1023
DOCX 121 кбайт
0 скачиваний
Оцените материал:

Настоящий материал опубликован пользователем Анкушева Ирина Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 6 лет и 4 месяца
Подписчики: 0
Всего просмотров: 28757
Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Программа для вычисления площади треугольника на языке C#Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.