Концентрационный треугольник pb bi sn (6 видео)

Микроструктура сплавов системы Bi – Pb – Sn

Лабораторная работа № 4

СТРУКТУРА ТРЕХКОМПОНЕНТНЫХ СПЛАВОВ СИСТЕМЫ

Bi – Pb – Sn

Современная техника не ограничивается использованием чистых металлов и двойных сплавов. В большинстве случаев для обеспечения требуемого комплекса свойств применяют многокомпонентные сплавы. Поэтому возникает необходимость изучения диаграмм состояния тройных и более сложных систем.

Диаграммы состояния трехкомпонентных систем можно представить в виде в виде треугольной призмы. Для изучения фазовых превращений в подобных системах строят политермические и изотермические разрезы, а также проекции поверхностей ликвидуса на плоскость концентрационного треугольника.

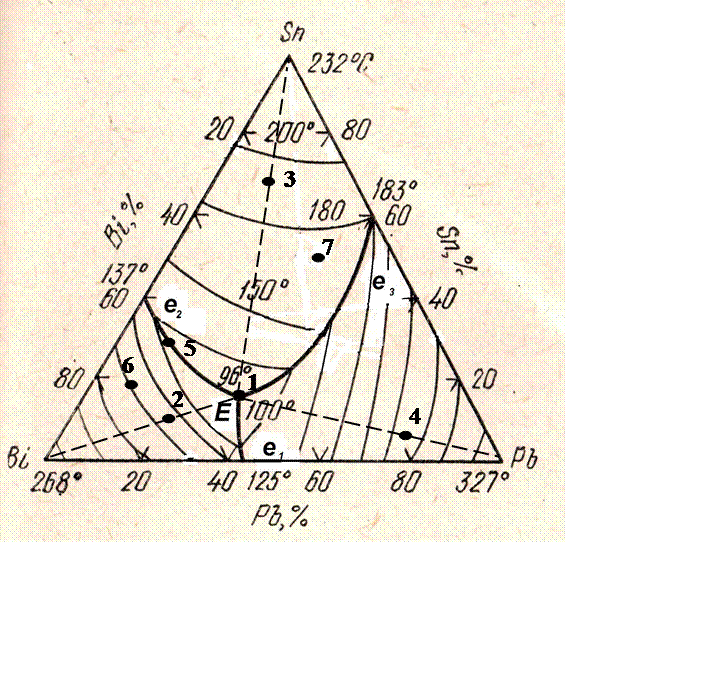
Рисунок 1.- Проекции поверхностей ликвидуса на плоскость концентрационного треугольника.

В качестве примера рассмотрим систему Bi – Sn –Pb, в структуре сплавов которой присутствует тройная эвтектика (рисунок 1). Обычно сплавы, содержащие эвтектику с температурой плавления ниже олова, называются легкоплавкими. Легкоплавкие компоненты подбирают в сочетаниях, обеспечивающих образование многофазной эвтектики. Примером является данная система.

Температуры плавления Sn, Bi и Pb равны соответственно 232, 268 и 327 о С. Температуры плавления двойных эвтектик равны: е₁ (46% Bi + 54%Рb) – 125 о С; е₂ (34%Вi + 66%Sn) – 137 о С; е₃ (38%Рb + 62%Sn) – 183 о С. Температура плавления сплава состава тройной эвтектики (32%Pb + 16%Sn, ост. Bi) – 96 о С. В четверной системе при добавке кадмия эвтектика плавится уже при 68 о С, а в пятикомпонентной системе с добавкой индия – при 47 о С (сплав Вуда).

Сплавы с эвтектикой применяют в качестве легкоплавких припоев, предохранительных пробок и вставок, материалов для анатомических слепков, заливки металлографических шлифов и т.п.

При изучении шлифов следует обратить внимание на то, что избыточные первичные фазы Sn, Bi и Pb, выделявшиеся при кристаллизации, отличаются между собой формой кристаллов и степенью травимости (рисунки 3-5). Наиболее мягкая фаза (свинец) имеет округлую форму кристаллов и выявляется в виде темной структурной составляющей, в то время как олово и висмут – ограненные кристаллы. Двойные эвтектики отличаются своим строением (морфологией) и выглядят по сравнению с тройной эвтектикой более светлыми (рисунки 5-9).

Задание. 1. Изучить структуры трехкомпонентных сплавов системыBi – Pb – Sn с помощью микроскопа и зарисовать их; указать фазовые и структурные составляющие.

2. Построить кривые охлаждения и зарисовать схему кристаллизации рассмотренных сплавов.

3. Выполнить сравнительный анализ структур избыточных фаз, двойных и тройных эвтектик, объяснить причины различного их строения.

Микроструктура сплавов системы Bi – Pb – Sn

Видео:Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Диаграммы состояния тройных систем

В системе, состоящей из трех компонентов, в отличие от двухкомпонентных, прибавляется еще одна независимая переменная – концентрация третьего компонента, поэтому диаграмма состояния должна строиться в трех координатах, т.е. в пространстве. Здесь обычно значения процентных содержаний (концентрации компонентов) наносятся на горизонтальные плоскости, а значения температур – по вертикали. Основанием такой пространственной фигуры является обычно равносторонний (правильный) треугольник, по которому определяют значения концентраций всех трех компонентов в любом сплаве системы. Такой треугольник – основание диаграммы состояний тройной системы – называется концентрационным (рис. 23).

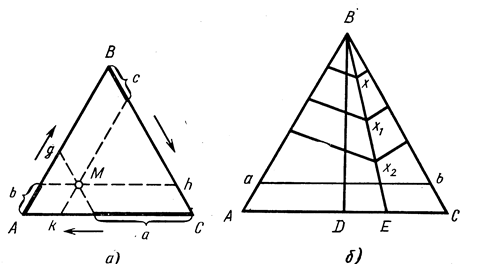
Рисунок 23 – Концентрационные треугольники тройной системы А-В-С

Метод отсчета состава сплава по концентрационному треугольнику заключается в следующем.

1 Через данную точку М внутри треугольника А-В-С проводят прямые, параллельные его сторонам. Отрезки на сторонах треугольника, заключенные между вершиной и точкой пересечения прямой, проведенной параллельно стороне треугольника, определяют количество того компонента, вершина которого противоположна стороне, параллельно которой проведена прямая. При таком методе отсчета необходимо следить, чтобы концентрация компонентов откладывалась в одном направлении (например, против часовой стрелки – см. рис. 23, а).

2 Другой способ. Вершины треугольника отвечают соответствующим чистым компонентам А, В и С. На сторонах треугольника будут находиться соответствующие двойные системы А – В, В – С и С – А, а все тройные сплавы (состоящие из трех компонентов) будут заключаться внутри треугольника, т.е. каждая точка в нем будет отвечать тройному сплаву определенного состава, и этот состав, т.е. концентрация компонентов в сплаве, определится по длине перпендикуляров, опущенных на стороны треугольника из точки, соответствующей составу взятого сплава. Основание: в равностороннем треугольнике сумма всех перпендикуляров, опущенных из любой точки на стороны треугольника, равна его высоте. Таким образом, если высоту треугольника разделить на 100 частей соответственно 100 % каждого компонента, а длины каждого из перпендикуляров в тех же единицах считать пропорциональными процентному содержанию компонентов в сплаве, то эти длины и будут определять концентрацию каждого из компонентов в сплаве, т.е. дадут его полный состав. Какой перпендикуляр какому компоненту соответствует, можно определить по фигуре: ведь каждая высота треугольника представляет перпендикуляр, определяющий 100 % компонента, расположенного в соответствующей вершине; поэтому все перпендикуляры, параллельные данной высоте, являются как бы частью этой высоты и определяют процент того самого компонента, 100 % которого определяются соответствующей высотой треугольника.

Следовательно, состав сплава, отвечающего любой точке треугольника, определяется длиной перпендикуляров, опущенных из этой точки на стороны треугольника, и каждый перпендикуляр соответствует процентному содержанию того компонента, который определяется высотой, параллельной данному перпендикуляру (см. рис. 23, б).

Тройные диаграммы строятся экспериментальным путем. Для этого, так же, как и в случае двойных сплавов, определяют критические температуры построением кривых охлаждения или нагрева и наносят на линию данного сплава, т.е. на перпендикуляр к плоскости в точке данного сплава. При соединении точек ликвидус получается поверхность ликвидус, а при соединении точек солидус получится поверхность солидус. Вид тройной диаграммы состояния зависит от того, какие фазы образуются в результате взаимодействия элементов в сплаве. Изучение их сложно. Рассмотрим наиболее простые случаи (рис. 24, 25).

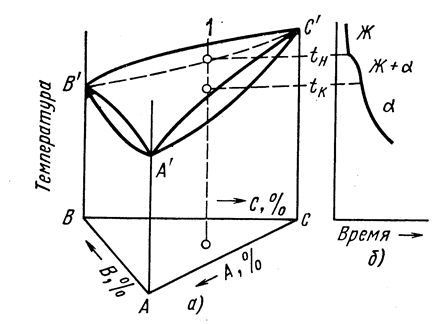
Рисунок 24 – Диаграмма состояния тройных сплавов с неограниченной

растворимостью компонентов в жидком и твердом состояниях (а)

и кривая охлаждения сплава 1 (б)

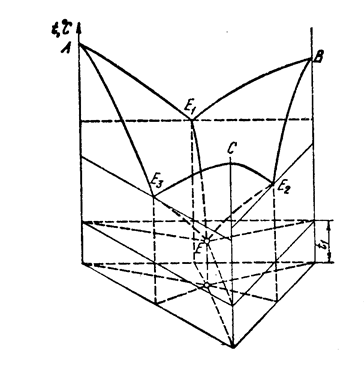
Рисунок 25 – Диаграмма состояния трехкомпонентной системы.

Компоненты не растворимы в твердом состоянии

и образуют тройную эвтектику (пространственное изображение)

Поверхность А / В / С / – поверхность ликвидус,вогнутая – поверхность солидус.

Для изучения таких диаграмм пользуются проекциями изотермических сечений, которые указывают для любого сплава температуру плавления, или развертками диаграмм (рис. 26).

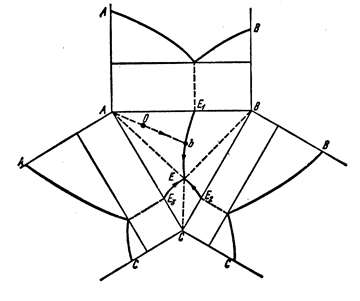
Рисунок 26 – Диаграмма состояния трехкомпонентной системы.

Компоненты не растворимы в твердом состоянии

и образуют тройную эвтектику (развертка)

Видео:Power BI для начинающих 25 - Закладки, Ленточная диаграммаСкачать

Рис. 9. (Продолжение) Занятие 4 ТРОЙНЫЕ СИСТЕМЫ СПЛАВОВ. СВОЙСТВА КОНЦЕНТРАЦИОННОГО ТРЕУГОЛЬНИКА Равновесная диаграмма сплавов из трех компонентов и

Ярослав Спечинский 5 лет назад Просмотров:

1 Рис. 9. (Продолжение) Занятие 4 ТРОЙНЫЕ СИСТЕМЫ СПЛАВОВ. СВОЙСТВА КОНЦЕНТРАЦИОННОГО ТРЕУГОЛЬНИКА Равновесная диаграмма сплавов из трех компонентов и одного внешнего параметра (температуры) требует для описания трехмерного графика и обычно имеет вид трехгранной призмы, в основании которой лежит концентрационный треугольник (рис. 10).

2 Рис. 10. Концентрационный треугольник Для выполнения заданий необходимо изучить свойства концентрационного треугольника и особенности применения правила отрезков в тройной диаграмме. Составы тройных сплавов из компонентов А, В и С указываются в плоскости равностороннего треугольника, на сторонах которого изображаются концентрации двойных сплавов, в вершинах располагаются компоненты (рис. 10). Свойства концентрационного треугольника 1. Сумма трех перпендикуляров Xa 1 + Xb 1 + Xc 1, опущенных из любой точки X внутри треугольника на его стороны, есть величина постоянная и равна высоте треугольника Вh. Если высоту Bh треугольника принять за 100 % сплава, то величины перпендикуляров будут определять содержание того компонента, к вершине которого направлено продолжение перпендикуляра. Например, величина перпендикуляра Xа 1 будет определять содержание в процентах компонента А. 2. Сумма отрезков Ab + Bc + Ca, отсекаемых на сторонах треугольника прямыми, проходящими через любую точку X внутри треугольника параллельно его сторонам, есть также величина постоянная, равная стороне треугольника. Если принять длину стороны треугольника за 100 % сплава, то состав тройного сплава выразится величинами отрезков Ca (% компонента A), Ab (% компонента В) и Bc (% компонента С). Из этого следуют некоторые свойства линий на концентрационном треугольнике: все сплавы, точки состава которых лежат на линии параллельной одной из его сторон, имеют постоянную концентрацию компонента на противоположной вершине (Пример на рис. 10 на линии aa’ лежат точки сплавов, которые содержат 33 % A, на bb’ 41 % B, на cc’ 26 % С); все сплавы, точки которых лежат на секущей, выходящей из вершины треугольника, содержат постоянное отношение концентраций компонентов, вершины которых лежат по обе стороны от этой линии (Пример на рис. 10 на линии Bf лежат точки сплавов, в которых % C % A Af = fc = 66 34, а на линии Bh % C : % A = 50 : 50. Так, если в точке на линии Bh в сплаве будет 60 % B, то содержание компонентов A и С будет поровну по 20 %). Исключением являются вершины, в которых всегда 100 % одного из компонентов. Так как в тройной системе % A + % B + % С = 100 %, то для нахождения положения точки сплава с известным химическим составом достаточно отложить на двух сторонах содержание двух компонентов (примерно, 41 % B и 26 % С на рис. 10). Провести через эти точки соответствующие параллели сторонам треугольника (линии bb’ и cc’). На пересечении этих линий лежит искомая точка сплава X. Правило отрезков Принцип применения правила отрезков в тройных сплавах такой же, как и в двойных сплавах (рис. 11). Рис. 11. Правило рычага Пусть заданы концентрации двух тройных сплавов Х и Y (рис. 11). Надо найти состав нового сплава K, который получится после сплавления 2 кг сплава X и 4 кг сплава Y. В соответствии с правилом отрезков, положение нового сплава К изобразится точкой, которая разделит отрезок XY на части KХ и KY обратно пропорцио-

3 нально весовым количествам сплавляемых сплавов: KX KY 4 = 2 (т.е. точка сплава будет лежать ближе к тому сплаву, которого добавляется больше по массе). Таким же образом можно найти концентрацию материала, получаемого из трех и более сплавов, путем последовательного парного расчета сплавления. Такие промежуточные материалы называют лигатурами. Индивидуальные задания к занятию Нанести на концентрационный треугольник три сплава (табл. 2). 4.2 Указать химический состав любого трехкомпонентного сплава X, который можно выплавить из этих сплавов (1, 2, 3 из табл. 2), и который из них нельзя изготовить (сплав Y). 2. Химический состав сплавов, % Вари-ант Сплав 1 Сплав 2 Сплав 3 Рb Bi Cd Pb Bi Cd Рb Bi Cd Определить расчетно-графическим способом химический состав материала Z, полученного смешиванием сплавов 1, 2, 3 (табл. 2) в количествах, указанных в табл При охлаждении 1 кг расплава (табл. 4) от температуры Т 1 до Т 2 из жидкой фазы выделились кристаллы чистого металла в количестве m грамм. Определить химический состав оставшейся жидкости. 3. Весовые соотношения сплавов Вариант Масса сплавов, кг Сплав 1 Сплав 2 Сплав

4 Расчет кристаллизации сплава Вари-ант Состав расплава, % m, кг Pb Bi Cd Sn Pb Bi Cd Sn , , , , , , ,2 Продолжение табл. 4 Вари-ант Состав расплава, % Pb Bi Cd Sn Pb Bi Cd Sn , , , , , , , , ,5 Занятие 5 m, кг ИЗОБРАЖЕНИЕ И АНАЛИЗ ДИАГРАММ СОСТОЯНИЯ ТРОЙНЫХ СПЛАВОВ Тройные диаграммы состояния изображаются несколькими способами: в пространстве (аксонометрия), в проекции на плоскость концентрационного треугольника или в виде политермических и изотермических разрезов. Пространственное изображение используется очень редко (в учебных целях). Для решения заданий по этой теме необходимо изучить диаграммы равновесия сплавов с неограниченной растворимостью компонентов в твердом состоянии, диаграммы состояния с тройной эвтектикой при отсутствии растворимости и с ограниченной растворимостью компонентов в твердом состоянии. В качестве примера рассмотрим диаграмму равновесия с тройной эвтектикой и отсутствием растворимости компонентов в твердом состоянии (рис.12). Боковые грани ее представляют двойные диаграммы между компонентами с двойными эвтектиками e AB, e AC и e BC, каждая из которых имеет свою температуру кристаллизации. Ликвидус диаграммы изображается тремя поверхностями начала затвердевания компонентов (A’ e AB e ABC e AC A’, B’ e BC e ABC e AB B’ и C’ e AC e ABC e BC C’). Эти поверхности пересекаются по тем кривым кристаллизации двойных эвтектик (e AB e ABC, e BC e ABC и e AC e ABC ). На «лепесток» B’ e BC e ABC e AB B’ начала кристаллизации компонента B нанесены изотермы (рис. 12).

5 Рис. 12. Пространственная диаграмма состояния с тройной эвтектикой Под «лепестками» расположены три двухфазные области (L + A, L + B, L + C), показанные на рис. 13, а. Сбоку они ограничены соответствующими двухфазными областями двойных диаграмм. Снизу двумя криволинейными линейчатыми (состоят из прямых отрезков изотерм, не лежащих в одной плоскости) поверхностями, которые смыкаются по линии a’ e ABC, лежащей в плоскости тройной эвтектики. Кристаллизация двойных эвтектик в тройной системе идет в диапазоне температур (трехфазные области L + A + B, L + B + C и L + A + C на рис. 13, б). Сбоку границами этих областей являются линии соответствующих двойных эвтектик (a» e AB b» на рис. 13, б) и описанные выше линейчатые поверхности. Снизу границей является плоскость тройной эвтектики a’b’c’. а) б)

6 в) Рис. 13. Схемы фазовых областей тройной диаграммы, когда компоненты не растворимы друг в друге в твердом состоянии: а L + А; б L + A + B; в A + B + C Поверхностью солидус диаграммы является изотермическая плоскость тройной эвтектики a’b’c’, где L Aтв + Bтв + Cтв. Кроме этого в солидус входят точки кристаллизации чистых компонентов A’, B’ и C’ и линии двойных эвтектик a» e AB b», b»’ e BC c» и c»’ e AC a»’. Ниже плоскости тройной эвтектики a’b’c’ расположена трехфазная область (A + B + C), представленная на рис. 13, в. На рис. 14 показана проекция системы Bi Pb Sn на плоскость концентрационного треугольника, заполненная структурами после полного охлаждения сплавов. На плоскость концентрационного треугольника этой системы спроектировались все поверхности кристаллизации различных фаз: три поверхности начала кристаллизации чистых компонентов: А е ] Е е 3 А начало выделения кристаллов Bi; B e 1 E e 2 B начало выпадения кристаллов Pb (на рис. 14, а закрашена); С е 3 Е е 2 С начало роста кристаллов Sn. три поверхности (в проекции три малых треугольника) начала кристаллизации двойных эвтектик: А Е В (эвтектика Bi + Pb); С Е В (эвтектика Sn + Pb); А Е С (эвтектика Bi + Sn); проекция плоскости начала и окончания кристаллизации тройной эвтектики (Pb + Sn + Bi) совпадает с концентрационным треугольником ABC. Структурные треугольники позволяют качественно и количественно описать формирование структуры любого тройного сплава. Рассмотрим это на примере сплава К (рис. 14, б). Температуру начала кристаллизации сплава можно определить по положению его точки К относительно проекций линий изотерм поверхности ликвидус (t L1, t L2 и др. на рис. 13, а). На рис. 14, а они показаны условно. При пересечении поверхности ликвидуса B e 1 E e 2 B (рис. 14, б) в процессе охлаждения из жидкой фазы состава точки К выделяются кристаллы Pb. При этом состав жидкой фазы изменяется от точки К в направлении точки b. Выделение первичных кристаллов Pb заканчивается при достижении поверхности двойных эвтектик С Е В, когда концентрация жидкой фазы достигает точки b. С началом кристаллизации двойной эвтектики Ж Sn + Pb состав жидкой фазы изменяется по линии E e 2 в направлении точки Е. В момент, когда сплав достигнет температуры кристаллизации тройной эвтектики, состав жидкой фазы определится точкой Е.

7 а) б) Рис. 14. Структурные области концентрационного треугольника тройной диаграммы Bi Pb Sn: а линейные; б плоские Рис. 15. Кристаллизация сплава К Жидкость такого состава затвердевает по уравнению тройной эвтектики Ж Sn + Pb + Bi при постоянной температуре, так как по правилу фаз Гиббса вариантность системы С = k f + 1 = = 0. К началу кристаллизации двойной эвтектики количественное соотношение фаз (Q ж + Q Pb ) выразится как Q Ж = Q Pb KB Kb

8 (на рис. 14, б это соотношение будет 80 % фазы Ж и 20 % фазы Pb). При кристаллизации двойной эвтектики Ж Sn + Pb количество каждой фазы будет определяться вершинами конодного треугольника C d 1 B (положение точки d 1 с понижением температуры будет меняться от точки b до точки E). Количественное соотношение фаз определится по правилу отрезков для конодного треугольника: Kd2 Kb1 Kc1 Q Ж = (отрезок d 1 d 2 проводят через точку d 1 параллельно стороне АВ); Q Pb = и Q Sn =. d1d2 Bb1 Cc1 Общее количество затвердевшей части сплава к этому моменту можно выразить как KE Q тв = = QPb + QSn. Ed 3 Kd3 При достижении сплавом температуры точки Е жидкой фазы по количеству останется Q ж =, и имен- Ed но она превратится в тройную эвтектику Ж Sn + Pb + Bi при постоянной температуре. Кривая охлаждения и структура сплава К показана на рис. 15. В практике для описания фазового состава и структуры тройных сплавов чаще применяют изотермические и политермические разрезы пространственной диаграммы состояния. Рассмотрим построение политермических разрезов на примере сечения тройной диаграммы Pb + Bi + Sn вертикальной плоскостью, которая проходит в концентрационном треугольнике по линии (рис. 16). Построение линии ликвидус. На рис. 16, а разрез пересекает плоскость тройной эвтектики по линии 1′-2′-3′ (нижняя часть диаграммы область Pb тв + Bi тв + Sn тв для простоты не показана). Пересечение боковых граней дает по две критические точки 1»’ и 3»’ начало кристаллизации Bi I на двойных диаграммах и точки 1» и 3», соответствующие температуре двойных эвтектик e AC и e AB. Температуры точек 1»’ и 3»’ оценивают по их положению на концентрационном треугольнике относительно проекций изотерм ликвидуса (на рис. 14, а, б сплав в точке К начинает кристаллизоваться, примерно, при температуре t L3 ). 3 а) б) Рис. 16. Построение политермического разреза тройной диаграммы Так как участки ликвидуса на двойных диаграммах выпуклые, имеем основание соединить точки 1»’ и 3»’ выпуклой кривой это будет линия ликвидуса в данном разрезе. Линией солидус в этом сечении будет 1» 1′ 2′ 3′ 3» (крайние точки это конец кристаллизации на двойной диаграмме). Линейчатые поверхности a»’ e AC e ABC a’ и a» e AB e ABC a’ режутся секущей плоскостью по линиям 1» 2′ и 3» 2′, соответственно. Таким образом, они выходят из одной точки 2′ на плоскости тройной эвтектики и расходятся каждая к своей двойной эвтектике, показывая начало ее кристаллизации. Полученный политермический разрез на рис. 16, б заполнен структурными составляющими. Следует отметить, что в сплаве 2, лежащем на пунктирной линии a’ t ABC, после выпадения первичных кристаллов висмута сразу кристаллизуется тройная эвтектика (это свойство таких сплавов). При построении более сложных сечений обычно пользуются не объемной диаграммой, а ее проекцией на концентрационный тре-угольник. Рассмотрим построение политермического разреза параллельного боковой грани тройной диаграммы (рис. 17). Пусть он задан условием 25 % Sn = const. Порядок выполнения: 1. Провести линию 25 % Sn = const на концентрационном треугольнике (см. занятие 4).

9 2. Обозначить все точки пересечения разреза с фазовыми линиями Спроектировать все эти точки на график в координатах температура ( С в масштабе) концентрация (на рис. 17 % Bi и % Pb). 4. Построение линии ликвидус. Плоскость разреза пересекает поверхность ликвидус по линии 1»’ 2» 4» 5»’. Сначала находим температуру этих точек (по положению точек 1, 2, 4 и 5 относительно проекций изотерм ликвидуса). Затем наносим их положение на графике и соединяем. 5. Построение линии солидус. Все тройные сплавы рассматриваемой системы должны заканчивать кристаллизацию образованием тройной эвтектики при постоянной температуре, поэтому линия солидус в сечении изобразится прямой линией 1′ 2′ 3′ 4′ 5′, проведенной параллельно плоскости концентрационного треугольника. Кроме этого на этом солидусе лежат точки 1» и 5», соответствующие концу кристаллизации на соответствующих двойных диаграммах. 6. Нахождение линий начала кристаллизации двойных эвтектик в разрезе. Рис. 17. Построение политермического разреза параллельного боковой грани тройной диаграммы Линейчатая поверхность начала кристаллизации двойной эвтектики (Bi + Sn) пересекается секущей по линии 1» 2» 3′. Линией начала кристаллизации двойной эвтектики (Pb + Sn) является 5» 4» 3′. Так как разрез не пересекает на концентрационном треугольнике область ABE, двойной эвтектики (Bi + Pb) в нем не будет. Следует отметить, что в сплаве 3, лежащем на пунктирной линии С Е, после выпадения первичных кристаллов олова сразу кристаллизуется тройная эвтектика. В сплавах 2 и 4 кристаллизуются только двойные и тройная эвтектики. Еще один пример с диагональным политермическим разрезом AP, который задается условием 25 % Sn : 75 % Pb = const, представлен на рис. 18.

10 Рис. 18. Построение диагонального политермического разреза тройной диаграммы

11 Порядок построения линий политермического разреза здесь аналогичен выше описанному: линия ликвидус A»’ 1» P»’, линия солидус A»’ A’ 2′ P’ P», линия начала кристаллизации двойных эвтектик A» 1» 2′ P». Примечательным фактом этого разреза является то, что несмотря на обилие критических точек на вертикали A»’ A» A’, затвердевание чистого висмута описывает лишь одна A»’ начало и конец кристаллизации. Индивидуальные задания к занятию Для сплава заданной концентрации определить температуру начала и окончания затвердевания, описать превращения, происходящие при кристаллизации, изобразить кривую охлаждения сплава, рассчитать количественное соотношение фаз и структурных составляющих (рис. 19, табл. 5). Вариант Рис. 19. Диаграмма состояния системы Sn Bi Pb 5. Состав тройного сплава, % вес Компоненты Pb Sn Bi Вариант Компоненты Pb Sn Bi Построить политермические разрезы (табл. 6) тройной диаграммы (рис. 19, 20) и заполнить области фазами и структурными составляющими.

12 Рис. 20. Диаграмма состояния системы Cd Pb Sn 6. Политермические разрезы, % вес Вариант Химсостав разреза Вариант Химсостав разреза Система Sn Bi Pb 1 10 % Sn = const 8 50 % Pb : 50 % Sn = const 2 18 % Sn = const 9 50 % Pb : 50 % Bi = const 3 30 % Sn = const % Bi : 50 % Sn = const 4 20 % Pb = const % Pb : 60 % Sn = const 5 40 % Pb = const % Pb : 70 % Bi = const 6 30 % Bi = const % Pb : 68 % Sn = const 7 52 % Bi = const % Bi : 25 % Sn = const Система Cd Pb Sn % Pb = const % Pb : 60 % Sn = const % Pb = const % Pb : 70 % Sn = const % Pb = const % Pb : 40 % Sn = const % Cd = const % Pb : 60 % Cd = const % Cd = const % Pb : 40 % Cd = const % Sn = const % Cd : 50 % Sn = const % Sn = const % Cd : 80 % Sn = const