- Онлайн калькулятор
- Периметр разностороннего треугольника
- Теория
- Периметр равнобедренного треугольника
- Теория
- Периметр равностороннего треугольника
- Расчёт периметра равнобедренного треугольника по основанию и высоте
- Определение равнобедренного треугольника
- Определение высоты треугольника
- Равнобедренный треугольник. Онлайн калькулятор
- Определение равнобедренного треугольника
- Теорема о равнобедренном треугольнике
- Свойства равнобедренного треугольника
- Признаки равнобедренного треугольника
- 1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
- 2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
- 3. Признак равенства равнобедренных треугольников по основанию и углу при основании
- Задачи и решения
- 🌟 Видео
Видео:Периметр равнобедренного треугольникаСкачать

Онлайн калькулятор
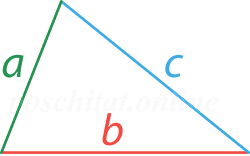
Периметр разностороннего треугольника
Чтобы вычислить чему равен периметр разностороннего треугольника вам нужно знать следующие параметры:
Введите их в соответствующие поля и узнаете чему равен периметр треугольника (Р).
Теория
Чему равен периметр разностороннего треугольника (P)?
Формула
Пример
К примеру, определим периметр разностороннего треугольника, у которого сторона a = 2 см, сторона b = 3 см, а сторона c = 4 см:
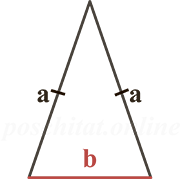
Периметр равнобедренного треугольника
Чтобы вычислить чему равен периметр равнобедренного треугольника вам нужно знать следующие параметры:
- длину двух равных сторон (a)
- длину основания (b)
Теория
Чему равен периметр равнобедренного треугольника (P)?
Формула
Пример
К примеру, определим периметр равнобедренного треугольника, у которого стороны a = 2 см, а сторона b = 3 см:
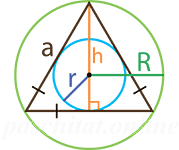
Периметр равностороннего треугольника
Чтобы вычислить чему равен периметр равностороннего треугольника вам нужно знать следующие параметры (либо-либо):
- длину трёх равных сторон (a)
- радиус описанной окружности (R)
- радиус вписанной окружности (r)
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

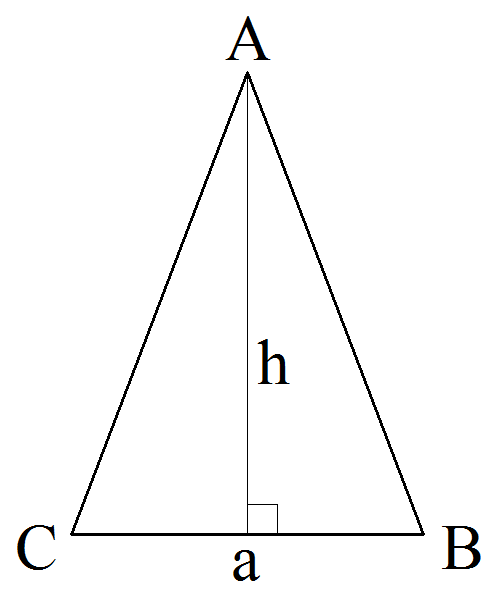
Расчёт периметра равнобедренного треугольника по основанию и высоте
Калькулятор рассчитывает периметр равнобедренного треугольника по основанию и высоте.
Периметром треугольника называется сумма всех длин его сторон.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Определение равнобедренного треугольника
Треугольник называется равнобедренным если две его стороны равны. Равные стороны называются боковыми, а третья основанием.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Определение высоты треугольника
Высотой треугольника называется перпендикуляляр опущенные с вершины треугольника к прямой содержащей противоположную сторону.
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Периметр равнобедренного треугольникаСкачать

Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
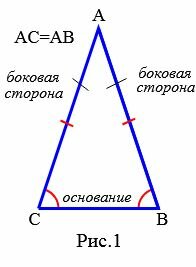
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Видео:№108. Периметр равнобедренного треугольника ABC с основанием ВС равен 40 см, а периметрСкачать

Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
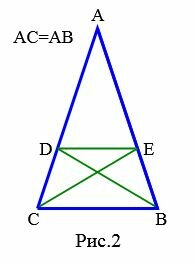 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| ( small CE=BD,) | (1) |
| ( small angle ACE=angle ABD.) | (2) |
Из ( small AB=AC) и ( small AD=AE ) следует:
| ( small CD=BE.) | (3) |
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что
| ( small angle ECB= angle DBC. ) | (4) |
Из (2) и (4) следует, что ( small angle B= angle C. )
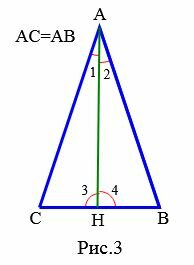 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )
Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Видео:САМАЯ ПОЛЕЗНАЯ,НУЖНАЯ В ЖИЗНИ ФОРМУЛА ВЫЧИСЛЕНИЯ БОКОВОЙ СТОРОНЫ ТРЕУГОЛЬНИКА РАВНОБЕДРЕННОГОСкачать

Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
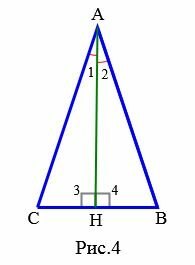
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
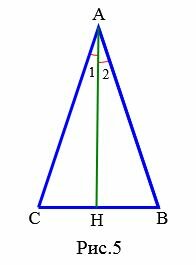
Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда
| ( small angle 1=angle2, ) ( small CH=HB. ) | (5) |
Применим теорему синусов для треугольника ( small AHC ):
| ( small frac = frac . ) | (6) |
Применим теорему синусов для треугольника ( small AHB ):
| ( small frac = frac . ) | (7) |
тогда, из (5), (6), (7) получим:
| ( small frac = frac . ) | (8) |
Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° — angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )
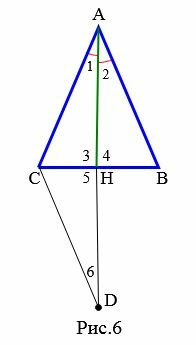 |
Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.
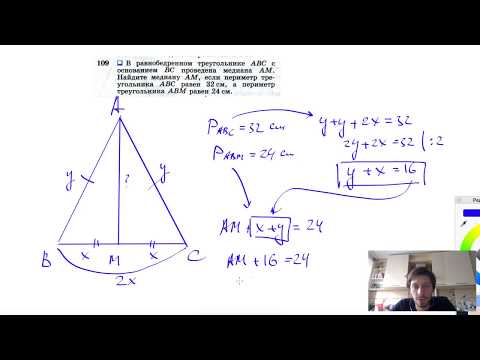
Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
Видео:Формулы равностороннего треугольника #shortsСкачать

3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Видео:Урок. Как найти периметр равностороннего треугольника. Математика 2 класс. #учусьсамСкачать

Задачи и решения
Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
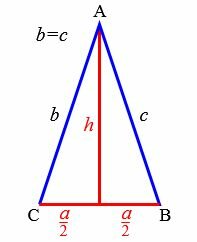 |
Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
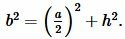 |
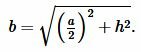 | (9) |
Подставляя значения ( small a ) и ( small h ) в (9), получим:
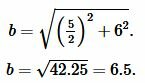 |
Боковая сторона ( small c ) равнобедренного треугольника равна:
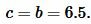 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
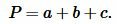 | (10) |
Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:
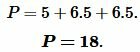 |
Найдем угол ( small B ) равнобедренного треугольника:
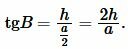 | (11) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:
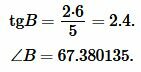 |
Тогда угол ( small C ) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
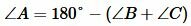 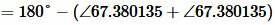 , , |
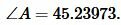 |
Площадь треугольника можно вычислить из формулы:
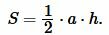 | (12) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:
🌟 Видео
Задачи на периметр труегольника. Геометрия 7 класс. Две задачи.Скачать

Хитрый периметрСкачать

ЕГЭ Математика Задание 6#27935Скачать

КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Равнобедренный треугольникСкачать