На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
- По формуле Герона
- Через основание и высоту
- Через две стороны и угол
- Через сторону и два прилежащих угла
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника через стороны
- Площадь равнобедренного треугольника через основание и угол
- Площадь равностороннего треугольника через стороны
- Площадь равностороннего треугольника через высоту
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь треугольника через радиус описанной окружности и три стороны
- Площадь треугольника через радиус вписанной окружности и три стороны
- Онлайн калькулятор. Площадь треугольника
- Найти площадь треугольника
- Ввод данных в калькулятор для вычисления площади треугольника
- Дополнительные возможности калькулятора вычисления площади треугольника
- Вы можете найти площадь треугольника если знаете следующие параметры:
- Теория. Площадь треугольника
- Формули площади треугольника
- Формула Герона
- Площадь треугольника онлайн
- Площадь треугольника по основанию и высоте
- Площадь треугольника по двум сторонам и углу между ними
- Площадь треугольника по стороне и прилежащим двум углам
- Площадь треугольника по трем сторонам. Формула Герона
- Площадь треугольника по трем сторонам и радусу описанной окружности
- 💥 Видео
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

Онлайн калькулятор. Площадь треугольника
Используя этот онлайн калькулятор, вы сможете найти площадь треугольника в зависимости от имеющихся у вас данных.
Воспользовавшись онлайн калькулятором для вычисления площади треугольника, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Найти площадь треугольника
Ввод данных в калькулятор для вычисления площади треугольника
В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.
Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади треугольника
- Между полями для ввода можно перемещаться нажимая клавиши и на клавиатуре.
Вы можете найти площадь треугольника если знаете следующие параметры:
- Длины трех сторон (используя формулу Герона)
- Длины двух сторон и значение угла между ними
- Длины стороны и опущенной на нее высоты
- Длины трех сторон и радиус описанной окружности
- Длины трех сторон и радиус вписанной окружности
- Длина полупериметра и радиус вписанной окружности
- Длина двух сторон и одного угла треугольника
- Длина одной стороны и двух углов треугольника
- Радиус описанной окружности и два угла треугольника
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Теория. Площадь треугольника
Формули площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 1 a · h 2 - Формула площади треугольника по трем сторонам
Формула Герона
S = √ p ( p — a )( p — b )( p — c )
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
| S = | 1 | a · b · sin γ |
| 2 |
| S = | a · b · с |
| 4R |
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b ,
r — радиус вписанной окружности,
R — радиус описанной окружности,
p — полупериметр треугольника.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Видео:№1020. Найдите площадь треугольника ABC, если: а) АВ = = 6√8 см, АС=4 см, ∠А=60°;Скачать
Площадь треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Площадь треугольника по основанию и высоте
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):
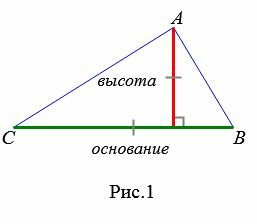 |
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
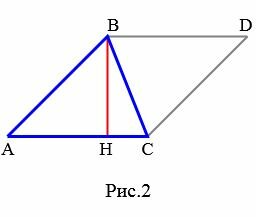 |
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
| ( small S= frac cdot AC cdot BH. ) |
Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:
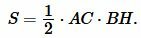  |
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
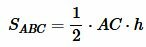 , , |
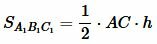 , , |
Обозначим через k отношение
| ( small k= frac . ) |
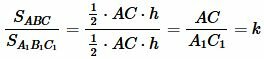 . . |
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
Видео:Как найти площадь треугольника без формулы?Скачать

Площадь треугольника по двум сторонам и углу между ними
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
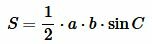 . . |
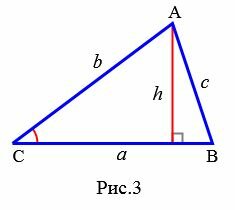 |
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
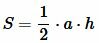 , , | (1) |
где h − высота треугольника.
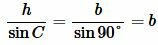 , , |
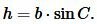 | (2) |
Подставляя (2) в (1), получим:
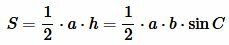 |
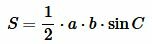  | (3) |
Видео:Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Площадь треугольника по стороне и прилежащим двум углам
Пусть известна сторона треугольника и две прилежащие углы (Рис.4).
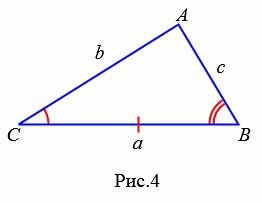 |
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
 | (4) |
Найдем сторону b используя теорему синусов:
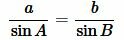 , , |
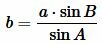 . . | (5) |
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
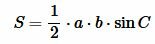 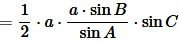 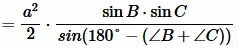 . . |
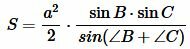 . . | (6) |
Видео:Как найти площадь треугольника, зная координаты его вершины.Скачать

Площадь треугольника по трем сторонам. Формула Герона
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
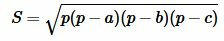 , , | (7) |
где a, b, c − стороны треугольника, а p − полупериод треугольника:
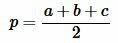 . . |
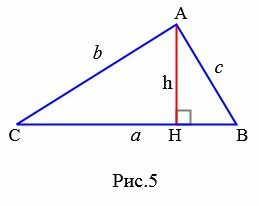 |
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
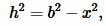 | (8) |
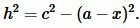 | (9) |
Из (8) и (9) следует:
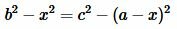 |
Откуда находим x:
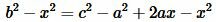 , , |
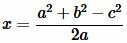 | (10) |
Подставляя (10) в (8) найдем h:
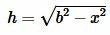 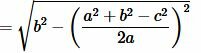 | (11) |
Тогда площадь треугольника равна:
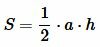 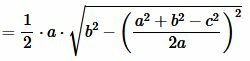 | (12) |
Преобразовав (12) получим формулу (7):
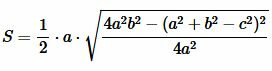 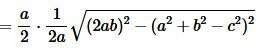 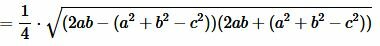 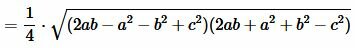 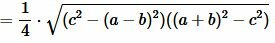 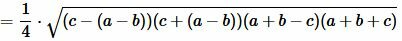 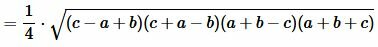 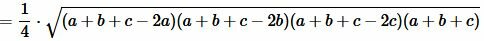 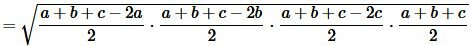 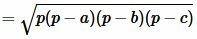 . . |
Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Площадь треугольника по трем сторонам и радусу описанной окружности
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac. )
💥 Видео
Задача 6 №27591 ЕГЭ по математике. Урок 59Скачать

Площади треугольникаСкачать
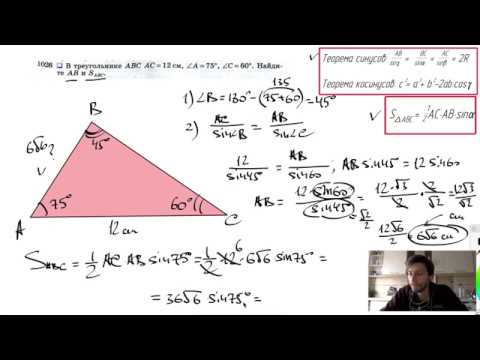
№1026. В треугольнике ABC АС = 12 см, ∠A= 75°, ∠C=60°. Найдите АВ и SABCСкачать
Решаем геометрию ОГЭ по математике 2024! Задание №15.Скачать

8 класс, 14 урок, Площадь треугольникаСкачать

Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

найти площадь треугольника. Формула Герона. Известны 3 стороны.Скачать

Самый простой способ нахождения площадиСкачать














