Какой угол треугольника наибольший

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Фигура	Рисунок	Формулировка
Треугольник
Большая сторона треугольника		Против большей стороны треугольника лежит больший угол
Больший угол треугольника		Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника		Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника		Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
		Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Сумма углов треугольника равна 180°

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

,

Треугольник
Большая сторона треугольника
	Против большей стороны треугольника лежит больший угол
Больший угол треугольника
	Против большего угла треугольника лежит большая сторона
Меньшая сторона треугольника
	Против меньшей стороны треугольника лежит меньший угол
Меньший угол треугольника
	Против меньшего угла треугольника лежит меньшая сторона
Длины сторон треугольника
	Углы треугольника
Внешний угол треугольника
Больший угол треугольника
Меньший угол треугольника
Теорема косинусов
Теорема синусов

Треугольник

Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.

Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Большая сторона треугольника

Свойство большей стороны треугольника:

Против большей стороны треугольника лежит больший угол

Больший угол треугольника

Свойство большего угла треугольника:

Против большего угла треугольника лежит большая сторона

Меньшая сторона треугольника

Свойство меньшей стороны треугольника:

Против меньшей стороны треугольника лежит меньший угол

Меньший угол треугольника

Свойство меньшего угла треугольника:

Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.

a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Углы треугольника

Свойство углов треугольника:

Сумма углов треугольника равна 180°

Внешний угол треугольника

Свойство внешнего угла треугольника:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Больший угол треугольника

Свойство большего угла треугольника:

Величина большего угла треугольника не может быть меньшей, чем 60°.

,

где α – больший угол треугольника.

Меньший угол треугольника

Свойство меньшего угла треугольника:

Величина меньшего угла треугольника не может быть большей, чем 60°.

,

где β – меньший угол треугольника.

Теорема косинусов

Теорема синусов

Свойство меньшего угла треугольника:

,

Какие значения может принимать: а) наибольший угол треугольника; б) наименьший угол треугольника; в) средний по величине угол треугольника?

Ваш ответ

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Вопрос: Как определить наибольший угол треугольника?

Как найти наибольший угол в треугольнике?

сначала используйте Закон косинусов, чтобы вычислить наибольший угол. затем используйте Закон синусов, чтобы найти другой угол. и, наконец, добавьте углы треугольника к 180 °, чтобы найти последний угол.

Как узнать, какой угол больше?

Сможете определить, какой угол самый большой? Как вы могли догадаться, наибольший угол будет противоположным 18, потому что это самая длинная сторона. Точно так же наименьший угол будет противоположен самой короткой стороне, 7. Следовательно, размер угла в середине будет противоположным 13.

Какой угол у треугольника самый большой?

Наибольший угол в 5 раз меньше наименьшего, поэтому наибольший угол равен 5 градусам. Таким образом, наименьший угол составляет 24 градуса.
.

слова	проверка
Наибольший угол треугольника в 5 раз больше наименьшего.	120 в пять раз больше 24? Да!

Как найти угол треугольника от наименьшего к наибольшему?

В любом треугольнике наименьший угол всегда поперек самой короткой стороны, а наибольший угол всегда поперек самой длинной стороны. В приведенном выше треугольнике ABC, поскольку угол A является наименьшим углом, сторона BC должна быть самой короткой стороной.

Как найти угол треугольника с двумя сторонами?

1. Шаг 1 Две известные нам стороны — Противоположная (300) и Соседняя (400).
2. Шаг 2 SOHCAHTOA сообщает нам, что мы должны использовать Tangent.
3. Шаг 3 Вычислить напротив / рядом = 300/400 = 0.75.
4. Шаг 4 Найдите угол на калькуляторе с помощью tan-1.

Какая сторона в прямоугольном треугольнике самая короткая?

В любом треугольнике самая длинная сторона противоположна наибольшему углу, а самая короткая сторона противоположна наименьшему углу. Таким образом, в прямоугольном треугольнике гипотенуза всегда является самой длинной стороной.

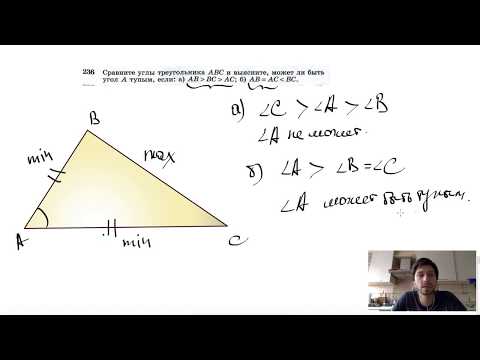
Какое правило поиска недостающей стороны треугольника?

Найти недостающую сторону прямоугольного треугольника довольно просто, если известны две стороны. Одна из наиболее известных математических формул — a2 + b2 = c2 a 2 + b 2 = c 2, известная как теорема Пифагора.

Какой угол противоположен самой длинной стороне?

Концепции. Самая длинная сторона треугольника противоположна наибольшему углу, а самая короткая сторона противоположна наименьшему углу. Неравенство треугольника: В любом треугольнике сумма длин любых двух сторон больше, чем длина третьей стороны. Теорема Пифагора: в прямоугольном треугольнике с гипотенузой c, a2 + b2 = c2.

Становится ли угол больше, если его линии длиннее?

Острые углы часто переоцениваются, что объясняется латеральными тормозными механизмами. … Однако в экспериментах 1 и 2 было обнаружено, что углы с более длинными плечами считаются большими.

Все ли треугольники равны 180 градусам?

Ответ положительный! Чтобы математически доказать, что сумма углов треугольника всегда равна 180 градусам, нам нужно установить некоторые основные факты об углах. Первый факт, который нам нужно рассмотреть, — это определение прямого угла: прямой угол — это просто прямая линия, отсюда и название.

Какое наибольшее количество тупых углов может содержать треугольник?

Джонсон З. Треугольник может иметь максимум 1 тупой угол.

Какая сторона треугольника самая длинная?

В прямоугольном треугольнике гипотенуза — это самая длинная сторона, «противоположная» сторона — это сторона, лежащая напротив заданного угла, а «смежная» сторона находится рядом с заданным углом.

Как определить угол?

Лучший способ измерить угол — использовать транспортир. Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.

Возможен ли треугольник со следующими углами и сторонами?

Нет, невозможно, чтобы сумма угла треугольника составляла 180 градусов.

🔥 Видео