Задача:
Построить треугольник по двум сторонам и углу между ними с помощью циркуля и линейки (без масштабных делений).
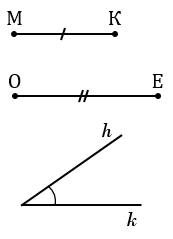
Дано: отрезки МК и ОЕ, 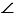
Построить 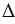
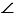
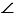
Решение:
С помощью линейки проводим прямую 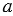
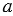
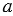
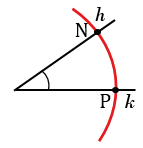
Далее строим угол ВАF равный углу hk. Для этого строим с помощью циркуля окружность радиуса МК с центром в вершине угла hk (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла hk обозначаем N и Р.
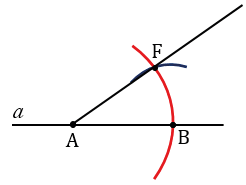
С помощью циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения данной окружности с окружностью радиуса МК с центром в точке А обозначаем F.
Далее, проводим луч АF с помощью линейки.
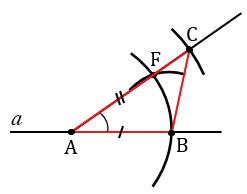
Затем, с помощью циркуля измеряем отрезок ОЕ и строим окружность радиуса ОЕ с центром в точку А (всю окружность строить необязательно, смотри, выделенное зеленым цветом). Точку пересечения данной окружности с лучом АF обозначаем С.
Теперь с помощью линейки соединяем точки В и С. Получаем треугольник АВС, в котором по построению АВ = МК, АС = ОЕ, 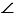
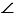
При любых данных отрезках МК, ОЕ и данном неразвернутом угле hk искомый треугольник построить можно. Прямую 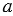
Поделись с друзьями в социальных сетях:
- Задачи на построение. 7-й класс, геометрия
- Построение треугольника по трем элементам
- Задачи на построение
- Изображение треугольника, если задана одна сторона и два прилегающих к ней угла
- Изображение треугольника, если заданы три стороны
- Изображение треугольника, если заданы две стороны и угол между ними
- 🎦 Видео
Видео:Построение угла с помощью транспортираСкачать

Задачи на построение. 7-й класс, геометрия
Разделы: Математика
Класс: 7
Цели урока:
- максимально донести до учащихся изучаемый материал;
- развивать мышление, память, умение свободно пользоваться циркулем;
- попытаться повысить активность и самостоятельность учащихся при выполнении заданий.
Оборудование:
- школьный циркуль
- транспортир,
- линейка,
- карточки для самостоятельной работы.
Тема урока: «Задачи на построение».
Сегодня мы будем учиться строить треугольники по трем заданным элементам с помощью циркуля и линейки.
Чтобы построить треугольник, нужно сначала уметь строить отрезок, равный заданному, и угол, равный заданному. Конечно, можно это сделать с помощью линейки с делениями и транспортира, но в математике требуется еще и уметь выполнять построения с помощью циркуля и линейки без делений.
Любая задача на построение включает в себя четыре основных этапа:
- анализ;
- построение;
- доказательство;
- исследование.
Анализ и исследование задачи необходимы так же, как и само построение. Необходимо посмотреть, в каких случаях задача имеет решение, а в каких – решения нет.
1. Построение отрезка, равного заданному.
2. Строим угол, равный заданному, с помощью циркуля и линейки.
А вот теперь перейдем к построению треугольников по трем элементам.
3. Построение треугольника по двум сторонам и углу между ними.
| Дано | Требуется построить | Построение |
 |  |  |
| 1. Построить угол А, равный заданному углу. 2. На одной стороне угла отметить точку С так, чтобы отрезок АС был равен заданному отрезку b. 3. На другой стороне угла отметить точку В так, чтобы отрезок АВ был равен заданному отрезку с. 4. Соединить с помощью линейки точки В и С. | ||
Построен треугольник АСВ по двум сторонам и углу между ними.


Самостоятельная работа к схеме 3.
Построить треугольник ВСН, если ВС = 3 см, СН = 4 см, 
Построить треугольник СДЕ, у которого ДС = 4 см, ДЕ = 5 см, 
Подсказка. Перед построением треугольника необходимо сделать «от руки» чертеж треугольника, где показаны все заданные элементы.
4. Построение треугольника по стороне и прилежащим к ней углам.
Дано
Требуется построить
Построение
2. Построить угол А, равный заданному.
3. Построить угол В, равный заданному.
Точка пересечения двух сторон углов А и В – вершина треугольника С.
Построили треугольник АСВ по стороне и двум заданным углам.


Самостоятельная работа к схеме 4.
Построить треугольник КМО, если КО = 6 см, К = 130є, О = 20є.
Построить треугольник ВСР, если С = 15є, Д = 50є, СД = 3 см.
5. Построение треугольника по трем сторонам.
Дано
Требуется построить
Построение
2. Из точки А провести часть окружности, радиус которой
равен заданному отрезку b.
3. Из точки В провести часть окружности, радиус которой
равен заданному отрезку a, обе окружности пересекаются в точке С.
Построили треугольник АСВ по трем сторонам.


Самостоятельная работа к схеме 5.
Построить треугольник ОДЕ, если ОД = 4 см, ДЕ = 2 см, ЕО = 3 см.
Построить треугольник МНО, если МН = 1 см, НО = 4 см, ОМ = 3 см.
После построения любого треугольника, самостоятельно провести доказательство того, что получившийся треугольник – искомый, и по возможности провести исследование.
Видео:Построение угла с помощью транспортира. 5 клСкачать

Построение треугольника по трем элементам
Видео:Построение углов заданной градусной мерыСкачать

Задачи на построение
Широкое распространение в геометрии получили задачи на построение. Суть этих задач состоит в следующем: при заданных начальных условиях нужно построить тот или иной геометрический объект при помощи линейки и циркуля. Разберем общие принципы решения данных задач:
Анализирование задачи. На этом этапе необходимо установить взаимосвязь между заданными условиями и объектом, который нужно изобразить. Результатом выполнения этого этапа является план решения задачи.
Построение. Согласно разработанного плана выполняется построение объекта.
Доказательство. На этом этапе необходимо доказать, что изображенная фигура полностью соответствует заданным условиям.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Изучение. На этом этапе выполняется анализ начальных условий и определение, при каких условиях задача решается одним способом, при каких двумя, а при каких – вовсе не решаема.
Разберем задачи на построение треугольника по трем различным начальным условиям.
Видео:№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать
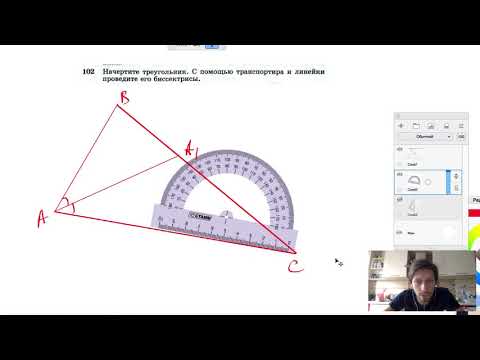
Изображение треугольника, если задана одна сторона и два прилегающих к ней угла
Задана одна сторон треугольника (BC) и прилежащие к ней углы (∝) и (β) , необходимо построить треугольник.
1. Анализируем условия. Необходимо построить треугольник (ABC) , имея одну сторону (BC) и углы (∠K= ∝ и ∠M= β) к ней прилежащие. Разработаем план решения задачи:
- Начертим прямую a, а на ней отмерим отрезок (BC) ;
- Изображаем угол (∠K= ∝) с центром в вершине (B) на стороне (BC) ;
- Изображаем угол (∠M= β) с центром в вершине (C) на стороне (BC) ;
- На пересечении лучей построенных углов получим точку (A) , соединяем ее с точками (C) и (B) , получаем отрезки (AC) и (AB) .
2. Строим треугольник
3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.
4. Изучение. Заданные углы могут быть построены и в противоположную сторону, соответственно мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма всех углов треугольника должна равняться 180 0 , если сумма углов (∝) и (β) будет равна или больше 180 0 , решения задача не будет иметь.
Видео:Построить угол 60°Скачать

Изображение треугольника, если заданы три стороны
Заданы три стороны треугольника (AB) , (AC) и (BC) , нужно построить треугольник.
1. Анализируем условия. Необходимо построить треугольник (ABC) , имея три стороны (AB) , (AC) и BC. Разработаем план решения задачи:
- Начертим прямую (a) , а на ней отмерим отрезок (AB) ;
- Чертим с помощью циркуля две окружности. Одна окружность будет с центром в точке (A) с радиусом (AC) , а вторая с центром в точке (B) с радиусом (BC) ;
- На пересечении окружностей мы получим точку (C) , соединяем ее с точками (A) и (B) , получаем отрезки (AC) и (BC) .
2. Строим треугольник:
3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.
Не нашли что искали?
Просто напиши и мы поможем
4. Изучение. Построенные окружности имеют две точки пересечения, поэтому мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма двух сторон треугольника всегда больше, чем третья его сторона, можно сделать вывод, если это условие не будет выполнено для заданных сторон, то задача не будет иметь решение.
Видео:Измерение угла с помощью транспортираСкачать

Изображение треугольника, если заданы две стороны и угол между ними
Заданы две стороны треугольника (AB) и (AC) , а также угол ∝ между ними, необходимо построить треугольник.
1. Анализируем условия. Необходимо построить треугольник (ABC) , имея стороны (AB) и (AC) , а также угол (CAB) , равный (∝) . Разработаем план решения задачи:
- начертим прямую (a) , а на ней отмерим отрезок (AB) ;
- отмеряем угол (MAB) , равный (∝) ;
- откладываем отрезок (AC) на прямой (AM) ;
- чертим третью сторону треугольника (CB) , соединяя точки (B) и (C) .
2. Строим треугольник:
3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.
4.Изучение. Прямая a бесконечна, поэтому таких треугольников можно изобразить очень много, но учитывая тот факт, что они все одинаковые, будем считать, что задача имеет одно решение. При условии, если угол (∝) будет равен или больше 180 0 , решения задача не будет иметь, так как сумма всех углов треугольника должна равняться 180 0 .
🎦 Видео
КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Построить угол 30°Скачать

Построение угла 120 градусов с помощью циркуля и линейки.Скачать

Построение треугольника, равного данномуСкачать
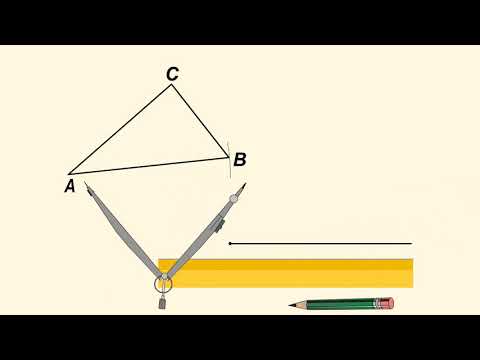
как пользоваться транспортиром?Скачать
Строим треугольник по трем сторонам (Задача 5).Скачать

Классный способ для разметки любого угла без транспортира.Скачать

Построить повернуть отрезок, линию под определенным нужным углом в Автокаде (AutoCad)Скачать

Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Угол. Градусная мера угла. 5 класс.Скачать

Транспортир. Измерение и построение углов. 5 класс.Скачать