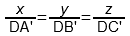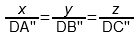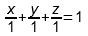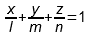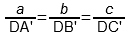На третьем курсе на занятиях по физической химии мы изучали различные диаграммы состояния. Особо запомнились своим довольно необычным видом такие диаграммы при постоянных температуре и давлении для систем, состоящих из трёх веществ, так как изображались они в виде равностороннего треугольника (т. н. «треугольник Гиббса-Розебома»), где каждая его точка соответствовала смеси какого-либо определённого состава (рис. 1, 2), а концентрации выражались как доли компонентов.
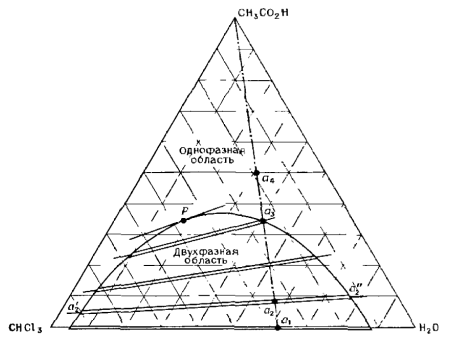
Рис. 1. Трёхкомпонентная система уксусная кислота – хлороформ – вода при комнатной температуре [1, с. 338].
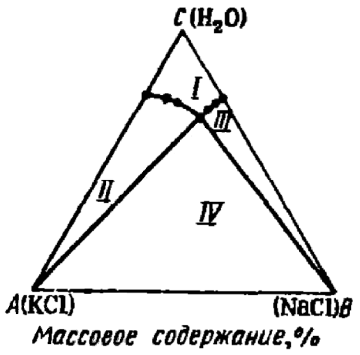
Рис. 2. Диаграмма растворимости KCl и NaCl в воде при 298 К [2, с. 485].
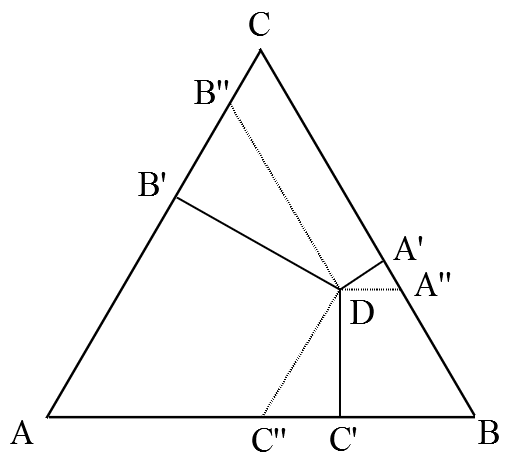
Также на лекциях нам рассказывали про два правила, по одному из которых каждой точке треугольника-диаграммы ставился в соответствие состав трёхкомпонентной смеси. Опишу кратко эти правила [3, с. 229] на примере системы из веществ A, B и C, мольные доли которых составляют x , y и z соответственно. Рассмотрим точку D внутри равностороннего треугольника △ABC (рис. 3). Какому соотношению x : y : z она соответствует?
Рис. 3. Определение состава смеси по правилам Гиббса и Розебома.
1) По правилу Гиббса высота треугольника принимается за единицу (или за 100%) и используется тот факт, что сумма длин перпендикуляров, опущенных из точки D на стороны треугольника равна его высоте. В этом случае концентрации (доли) компонентов пропорциональны длинам этих перпендикуляров:
x : y : z = DA’ : DB’ : DC’
2) По правилу Розебома за единицу (за 100%) принимается длина стороны треугольника, при этом из точки D проводятся отрезки, параллельные каждой из его сторон (на рис. 3 это DA», DB», DC»). Сумма их длин равна стороне треугольника и выполняется следующее соотношение:
x : y : z = DA» : DB» : DC»
или в иной записи
Легко видеть, что правила Гиббса и Розебома нисколько не противоречат друг другу:
x : y : z = DA’ : DB’ : DC’ = DA» : DB» : DC»
Это обусловлено тем, что △DA’A», △DB’B» и △DC’C» являются подобными (как треугольники с равными углами: ∠DA’A» = ∠DB’B» = ∠DC’C» = 90°; а ∠DA»A’ = ∠DB»B’ = ∠DC»C’ = 60°, поскольку DA» || AB, DB» || BC, DC» || AC).
Простого запоминания описанных правил вполне хватило для подготовки к сдаче экзамена, тем более дальнейшая жизнь сложилась так, что за все последующие годы с диаграммами состояния мне иметь дело особо-то и не доводилось. Тем не менее в те времена появилось ощущение, что что-то в этих правилах определения состава системы меня смущает и спустя год я понял, что же именно. Дело было в следующем. Очевидно, что доли компонентов системы связаны между собой соотношением
однако из такого равенства неизбежно следует, что для графического изображения множества точек, координаты которых удовлетворяют такому равенству, необходимо использовать трёхмерное пространство, потому что переменных в уравнении три, но при этом треугольник Гиббса-Розебома – это именно треугольник, то есть плоская (двумерная) фигура. Почему так? В итоге до меня дошла очень простая вещь: если переписать (3) как
то получается известное из аналитической геометрии «уравнение плоскости в отрезках», которое в общем виде записывается так:
где l , m и n – точки, в которых данная плоскость пересекает оси абсцисс, ординат и аппликат соответственно. Отсюда получается, что треугольник Гиббса-Розебома располагается именно в плоскости, описываемой уравнением (4). Можно сказать иначе: поскольку каждая из величин x , y , z принимает значения от 0 до 1 (потому что это доли компонентов в смеси), то треугольник Гиббса-Розебома является расположенным в первом октанте графиком функции
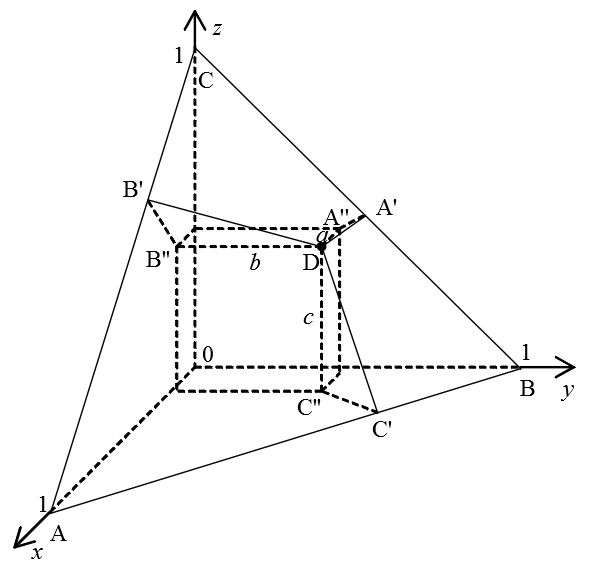
Из этого факта как раз и следует, что для построения диаграммы состояния трёхкомпонентной системы вполне достаточно плоского изображения. А ещё любопытно здесь другое. Взгляните на рис. 4 – на нём изображён треугольник Гиббса-Розебома в «трёхмерном» представлении.
Рис. 4. Треугольник Гиббса-Розебома, представленный как график функции z = 1 – x – y .
В △ABC выбрана точка D, от которой к сторонам этого треугольника проведены перпендикуляры DA’, DB’, DC’. Сама точка D имеет координаты ( a , b , c ), численные значения которых являются концентрациями входящих в состав смеси компонентов. Вершины △ABC с точкой начала координат образуют тетраэдр и из симметрии данного геометрического тела следует, что двугранные углы, образованные плоскостью △ABC и координатными плоскостями, равны. При этом в соответствии с теоремой, обратной теореме о трёх перпендикулярах , получается, что A’A» ⊥ BC, B’B» ⊥ AC, C’C» ⊥ AB, следовательно ∠DA’A», ∠DB’B» и ∠DC’C» являются линейными углами соответствующих двугранных углов, и значит они равны между собой. Отсюда вытекает, что △DA’A», △DB’B» и △DC’C» – подобные, из чего напрямую получается соотношение для правила Гиббса, аналогичное (1):
В связи с этим мне в голову уже давно закралась следующая мысль: а может создатели диаграмм состояния, когда разрабатывали способы наглядного преставления характеристик трёхкомпонентых систем, руководствовались схожими соображениями – про уравнение плоскости «в отрезках», про получающиеся при этом подобные треугольники и т. д.? Не удивлюсь, если такое действительно было опубликовано тем же самым Дж.У. Гиббсом в своих научных работах, а теперь, спустя более века и став классикой, успело подзабыться. В учебниках по физической химии, на которые я выше ссылался, и в ряде других [5, с. 422; ; 7, с. 401], сведений, подтверждающих приведённые догадки, нет – такую информацию нужно искать специально, но сначала необходимо суметь заставить себя заняться подобными поисками.
Кстати, схожая ситуация наблюдается и в отношении «правила креста» – очень легко отыскать литературу и сайты, где подробно рассказывается как решать задачи на смешение растворов с использованием этого правила, а вот материала, в котором описано откуда именно это правило берётся (то есть его математическое обоснование), мне обнаружить не удалось – пришлось восполнять этот пробел самостоятельно написанием соответствующей заметки.
- Эткинс П. Физическая химия. Том 1. М.: Мир, 1980. – 586 с.
- Физическая химия. В 2 кн. Кн. 1. Строение вещества. Термодинамика. Учеб. для вузов / Под ред. К.С. Краснова – 3-е изд., испр. – М.: Высшая школа, 2001. – 512 с.
- Карякин Н.В. Основы химической термодинамики: Учеб. пособие для вузов. Нижний Новгород: Издательство ННГУ им. Н.И. Лобачевского; М.: Издательский центр «Академия», 2003. – 464 с.
- Геометрия: Учеб. для 10-11 кл. сред. шк. / Л.С. Аганасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1992. – 207 с.
- Курс физической химии, том 1 / Под ред. Я.И. Герасимова. М.: Химия. 1964. – 624 с.
- Карапетьянц М.Х. Химическая термодинамика: Учебное пособие. Изд. 4-е. М.: Книжный дом «ЛИБРОКОМ», 2013. – 584 с.
- Киреев В.А. Курс физической химии. Изд. 3-е, перераб. и доп. М.: Химия, 1976. – 775 с.
Видео:Треугольник Гиббса. 2 часть. Задача. Метод РозебомаСкачать

Правило фаз Гиббса
Содержание:
Правило фаз (или правило фаз Гиббса) — соотношение, связывающее число компонентов, фаз и термодинамических степеней свободы в равновесной термодинамической системе. Роль правила фаз особенно велика при рассмотрении гетерогенных равновесий в многофазных многокомпонентных системах.
На странице -> решение задач по химии собраны решения задач и заданий с решёнными примерами по всем темам химии.
Видео:Метод РозебомаСкачать

Правило фаз Гиббса
Правило фаз Гиббса утверждает, что число степеней свободы С равновесной термодинамической системы равно разности между числом компонентов К и числом фаз Ф, плюс число факторов п, влияющих на равновесие.
Независимые компоненты и степени свободы системы
Представления о гомогенных и гетерогенных системах и фазах, изложенных в предыдущей главе, следует дополнить понятиями о компонентах и степенях свободы. Компонентами называют индивидуальные вещества системы, концентрации которых определяют состав всех ее фаз, т. е. веществ в системе может быть больше, чем требуется для описания состава всех ее фаз. Например, при установлении равновесия
система состоит из трех веществ, но для описания состава всех трех фаз достаточно знать любые два, их называют независимыми компонентами; состав третьей фазы легко определить, используя уравнение вещественного баланса. Из приведенного примера следует: число независимых компонентов равновесной системы равно общему числу индивидуальных веществ минус число связывающих их уравнений. При наличии химических реакций число независимых компонентов системы меньше числа индивидуальных веществ. Если же между веществами нет химического взаимодействия, то числа независимых компонентов и индивидуальных веществ совпадают (например, воздух состоит из такого же числа независимых компонентов, сколько сортов молекул входит в его состав).
Степенями свободы (С) равновесной системы называют те параметры, которые можно произвольно изменять, не меняя числа и природы фаз системы. Степенями свободы могут являться концентрации реагирующих веществ в фазах переменного состава (растворах), давление, температура.
Число степеней свободы определяют разностью между общим числом независимых переменных системы и числом уравнений, их связывающих. В приведенном выше примере общее число переменных равно двум (температура и давление С02 или его концентрация), уравнение одно, следовательно, число степеней свободы С данной системы равно: 2—1 = 1.
Количественное соотношение между числами степени свободы (С), фаз (Ф) и независимых компонентов (К), получившее название правила фаз, выведено В. Гиббсом (1876), оно имеет вид
Здесь 2 — число переменных параметров системы (давление и температура). Использование этого правила помогает при изучении химических реакций и равновесных систем.
Рассмотрим некоторые конкретные примеры.
Пример 1. Система представлена равновесием
Число независимых компонентов К равно разности числа индивидуальных веществ и числа уравнений, их связывающих, следовательно,

Связь 

Пример 2. Пусть система представлена равновесием 
Число независимых компонентов в ней равно

Это легко понять, если записать выражение температурной зависимости константы равновесия:

Следовательно, чтобы определить значение любой из переменных, нужно задать значения остальных трех.
Пример 3. Пусть система представлена ненасыщенным водным раствором хлористого натрия NaCl. В растворе, помимо молекул воды 

Эта однофазная система представлена тремя индивидуальными фермами соединений и одним уравнением, отсюда число независимых компонентов в этой однофазной системе равно
Поскольку газовая фаза (пар над раствором) не входит в рассматриваемую систему (по условию), то в выражении правила фаз Гиббса число параметров должно стать на единицу меньше, т. е. 
Однокомпонентные системы
Наиболее просты системы, состоящие из одного компонента. Каждая однокомпонентная система представлена единственным веществом, находящимся в различных агрегатных состояниях. Так, например, вода может существовать в парообразном, жидком и кристаллическом состояниях, каждое из которых устойчиво в определенных интервалах температуры и давления.
Переменными параметрами . однокомпонентных систем могут служить только давление и температура, поскольку состав фаз по условию постоянен. Поэтому состояние однокомпонентных систем может быть представлено в виде зависимости давления от температуры:

Графическое изображение такой зависимости получило название диаграммы состояния или фазовой диаграммы
состояния, поскольку состав фаз в однокомпонентной системе одинаков и при изменении условий не меняется.
Давление пара в процессах па рообра зова ни я уста на вл ивается и над твердыми, и над жидкими веществами:

Характер этой функциональной зависимости приведен на графике рис. 7.1. Точка плавления кристаллической фазы находится .совместным решением приведенных выше уравнений; исходя из условия равенства жидкой и кристаллической фаз должно выполняться условие 
При переходе из кристаллического состояния в пар (сублимация) степень разупорядоченности движения частиц больше, чем при испарении (в жидкости беспорядочность движения частиц больше, чем в кристаллах), поэтому величина 
Поскольку температура может принимать только значения Т > 0, величина 
Точно так же обстоит дело с полиморфными превращениями, если они есть.
Зависимость температуры плавления чистых веществ от давления p = fT можно определить уравнением Клаузиуса— Клайперона (приближенная форма):
В этом уравнении 


На рис. 7.2, а, б показано, что каждому из условий соответствует определенный наклон линии р = f(Т). Крутой ход кривых в равновесии между двумя конденсированными фазами объясняют незначительной разностью
Рассмотрим в качестве примера однокомпонентную систему вода—лед—пар. С точки зрения правила фаз Гиббса для такой системы 
Равновесие двух фаз (испарение, сублимация) характеризуется одной степенью свободы (произвольны давление или температура). Двухфазные превращения описываются следующими уравнениями:


При использовании этих данных на рис. 7.3 построен график зависимости р =f(Т), получивший название диаграммы’; состояния воды. Линии (а), (b) и (с) отвечают равновесиям двух фаз: твердое вещество— пар; твердое вещество— жидкость; жидкость— пар соответственно. Точка пересечения трех кривых носит название тройной точки, она отвечает равновесию всех трех фаз, а участки диаграммы I, II и III отвечают однофазному равновесию с тремя степенями свободы. Линия (b) имеет отрицательный наклон, соответствующий отрицательному значению 
Двухкомпонентные системы
Перейдем к характеристике более сложных, двухкомпонентных систем. С точки зрения правила фаз число степеней свободы в системах с К = 2 может максимально быть равным 3, если Ф= 1. Это означает, что кроме таких переменных параметров системы, как давление и температура, появляется третий— концентрация раствора. Примером однофазных систем переменного состава, образованных двумя и более независимыми компонентами, служат растворы. Растворы образуются во всех агрегатных состояниях. Они могут быть газообразными, жидкими и твердыми.
Все газы в любых соотношениях между собой неограниченно растворимы. Только при низких температурах и очень высоких давлениях в некоторых газовых смесях наблюдается расслоение. В жидком состоянии ограничение растворимости наблюдают довольно часто. Однако с повышением температуры растворимость обычно возрастает, так что многие жидкие смеси, расслоенные на две фазы, с повышением температуры становятся однофазными. Наиболее важные группы жидких растворов следующие:
1) водные, неводные и органические растворы;
2) солевые расплавы галогенидных, кислородных и сульфидных соединений (при высоких температурах);
3) расплавы металлов (при высоких температурах).
В твердом состоянии ограничение в растворимости также имеет место. Известны три типа твердых растворов: замещения, внедрения и вычитания. Твердые растворы замещения обычно образуются двумя или несколькими различными элементами, так что в кристаллической структуре места атомов одного элемента неупорядоченно замещаются атомами второго элемента. В результате распределение каждого из элементов оказывается хаотическим, а соотношение между количествами атомов того и другого сорта — произвольным. Примерами твердых растворов замещения служат сплавы меди и никеля или смешанные кристаллы хлористого и бромистого натрия. Твердые растворы внедрения получают чаще всего при растворении небольших по размеру атомов неметаллов в металлической решетке, например раствор углерода в железе. В этом случае атомы неметаллов (Н, В, С, О и др.) хаотически и в произвольных соотношениях располагаются в промежутках между атомами металла.
Твердые растворы вычитания, или дефектные структуры, характеризуются наличием пустот, которые размещаются хаотически и создают беспорядок в расположении мест, занятых атомами элементов. Примером таких структур служит сульфидный минерал пирротин, монотонно изменяющий свой состав в пределах
Общая характеристика растворов
Процесс растворения— сложный физико-химический акт, а не простое распределение частиц одного вещества между частицами другого, которое в какой-то степени применимо для описания разреженных газовых смесей. В жидких и твердых растворах частицы растворителя и растворенного вещества непосредственно взаимодействуют между собой и находятся на таких коротких расстояниях, как и в химических соединениях. Взаимодействие молекул растворителя с растворяемым веществом зависит от сил разнообразной природы, за счет которых в растворе образуются устойчивые комплексные и полимерные соединения, способные существовать вне раствора,— сольваты, а в случае водных растворов—гидраты.
Одна из важнейших количественных характеристик растворов, связанная через закон действующих масс с энергетикой процессов растворения,— концентрация раствора. Поэтому целесообразно вспомнить некоторые наиболее используемые способы выражения концентраций, кроме уже упомянутых молярности и молярной доли следует знать массовую и объемную доли, моляльную концентрацию (моляль-ность), титр.
Поскольку процессы растворения имеют сложную химическую природу, законы, определяющие растворение и отражающие природу растворов, сложны. Для упрощения введено понятие идеального раствора, простейшими примерами которого могут служить разреженные газы. В реальных газах соотношение между объемом, давлением и температурой описывается уравнением Ван-дер-Ваальса
В этом уравнении слагаемые 

Составляя смеси таких газов, можно убедиться в том, что для их взаимодействия справедливо условие 
Газовые растворы, которые образуются из составляющих их частей с нулевым тепловым эффектом, а объем их смеси в точности равен сумме объемов частей, получили название идеальных.
Для жидких и твердых растворов также существует понятие идеальности, в общем виде оно может быть сформулировано следующим образом: идеальными называют растворы, которые образуются из составных частей при выполнении условий
Примерами идеальных растворов могут служить газовые смеси изотопов, а также все разбавленные растворы. И действительно, добавление к растворителю небольшого количества растворяемого вещества мало изменяет свойства растворителя и раствора, и условие идеальности (7.2) справедливо. Но свойства растворяемого вещества в таком растворе далеки от идеальных.
Концентрированные растворы но свойствам не близки к идеальным, однако для получения грубой качественной картины их можно описывать с помощью модели идеальных растворов. Для строгого решения производственных и научных задач требуется обязательное введение поправок на реальность.
Услуги по химии:
Лекции по химии:
Лекции по неорганической химии:
Лекции по органической химии:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Треугольник Гиббса. Изучение взаимной растворимости в жидкой трехкомпонентной системе.Скачать

Содержание (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Для определения состава трехкомпонентной системы пользуются следующими свойствами прямых, проведенных в треугольнике Гиббса-Розебома:
1. Все точки, лежащие на прямой, параллельной стороне треугольника, отвечают растворам с одинаковым содержанием компонента, расположенного в противоположной вершине, и с изменяющимся количеством двух других.
Например, на линии fde’g (рис. 1.За) концентрация вещества А постоянна и равна 30%;
2. На прямой, проходящей через вершину треугольника, например на линии Ае (рис. 1.За),отношение концентраций компонентов В и С одинаково и равно в данном случае отношению отрезков Се: Be = 7:3.
Для нахождения состава раствора, отвечающего точке d на диаграмме, достаточно через данную точку провести линии, параллельные сторонам треугольника. Отрезки, отсеченные этими линиями на сторонах треугольника, укажут содержание соответствующих компонентов. Отрезок, gВ (или fC) соответствует 30% вещества А. Отрезок Аb, отсекаемый на стороне АС, линией, параллельной стороне АВ, отвечает 50% вещества С. Концентрация вещества В равна 20%.
Рис.1.3 а) Изображение состава трехкомпонентной системы с помощью треугольника Гиббса-Розебома. б) Диаграмма растворимости трех жидкостей, две из которых (В и С) взаимно нерастворимы, а третья (А) неограниченно растворима в первых двух.
На рис. 1.3.б представлен вид диаграммы — изотермы растворимости трёх жидкостей для случая, когда система состоит из двух (С и В) взаимно нерастворимых компонентов и третьего (А), неограниченно растворимого в каждом из первых двух.
Внутри треугольной диаграммы состояния имеются две области — однофазная и двухфазная, а линия, разделяющая эти две области, характеризует составы равновесных насыщенных растворов. Любая фигуративная точка внутри двухфазной области описывает суммарный состав системы, которая распадается на две фазы, различающиеся по составу. Их состав можно определить, проведя ноду kxqo. Например, в точке х в равновесии находятся насыщенные растворы, соответствующие на диаграмме точкам k и q. Все продолжения нод для такой системы сходятся в одной точке вне треугольника, как показано на рис. 1.3.б (правило Тарасенкова)
Число степеней свободы для трехкомпонентной системы при постоянных температуре и давлении рассчитывается по формуле:
Работа 3. Изучение взаимной растворимости трехкомпонентной системы
Цель работы: Определение составов насыщенных растворов из трех компонентов и построение диаграммы — изотермы растворимости.
1. Получить у лаборанта 3 бюретки, 10 сухих пробирок, склянки с тремя жидкостями одного из указанных в табл. 1.3 наборов, стакан для слива и бланк с треугольником Гиббса-Розебома.
2. Закрепить бюретки на штативе, подписав их названиями веществ. Налить соответствующие вещества в бюретки и установить их уровни на нуле.
3. Для веществ В и С, которыми будет производиться титрование для определения начала расслаивания системы, определить объем одной капли. Для этого налить в стакан из бюретки 20 капель вещества и определить их суммарный объем по делениям на бюретке. Разделив этот объем на число капель, рассчитать объем одной капли.
Таблица 1.3
📽️ Видео
Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

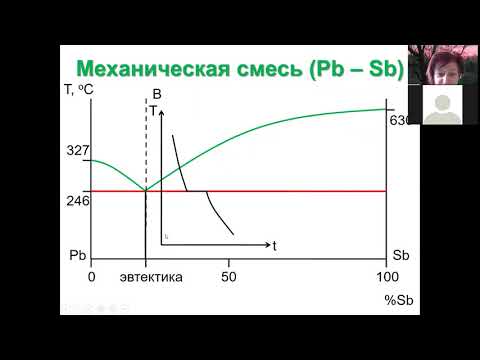
09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
Свободная энергия Гиббса. 10 класс.Скачать

Треугольник ПаскаляСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Бином Ньютона. 10 класс.Скачать

Математические секреты треугольника ПаскаляСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Угольник Свенсона. 7 функций в домашних условиях.Скачать

Зачем нужен треугольник Паскаля (спойлер: для формул сокращённого умножения)Скачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

09 Фазовые диаграммы 2 правило фазСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Фазовые диаграммыСкачать

Треугольник ПаскаляСкачать

7. Правило фазСкачать

Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать