Как найти высоту треугольника параллелограмма

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Видео:Задача на нахождение высоты параллелограммаСкачать

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Видео:Геометрия 8 класс (Урок№9 - Площадь параллелограмма.)Скачать

Параллелограмм

Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.

Все параллелограммы обладают следующими свойствами:

противоположные стороны равны:

противолежащие углы равны:

сумма углов, прилежащих к одной стороне, равна 180°:

в точке пересечения диагонали делятся пополам:

каждая диагональ делит параллелограмм на два равных треугольника:

точка пересечения диагоналей — это центр симметрии параллелограмма:

Точка O — это центр симметрии.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Высота

Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, — высотой.

AD — это основание параллелограмма, h — высота.

Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.

Видео:Как найти высоту треугольникаСкачать

Площадь

Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:

Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ΔABE и ΔDCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.

Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:

Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.

Общая формула площади параллелограмма:

где S — это площадь параллелограмма, a — основание, h — высота.

Видео:как найти диагональ.Скачать

Найти высоты параллелограмма и угол между ними

Высота — перпендикуляр исходящий из вершины угла на противоположенную сторону

a , b — стороны параллелограмма

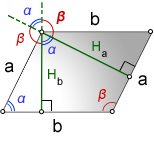
H _b — высота на сторону b

H a — высота на сторону a

α , β — углы параллелограмма

Формулы длины высоты параллелограмма, через сторону и угол, ( H _b , H a ):

Острый угол пересечения высот, равен острому углу параллелограмма.

Тупой угол пересечения высот, равен тупому углу параллелограмма.

📸 Видео

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Опорная задача о подобных треугольниках при пересечении высот | Планиметрия 84 | mathus.ru #егэ2024Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

✅ Площадь параллелограмма. Решаем задачу из ЕГЭСкачать

Вычисляем высоту через координаты вершин 1Скачать

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

8 класс. Площадь параллелограмма. Геометрия.Скачать

Площадь параллелограмма, треугольника, трапецииСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

8 класс, 14 урок, Площадь треугольникаСкачать

Геометрия 8 класс. Площадь параллелограммаСкачать