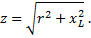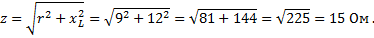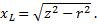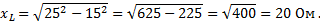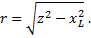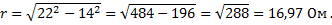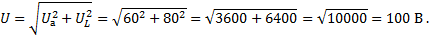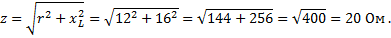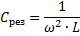В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Видео:R, L, C в цепи переменного тока/Треугольник сопротивлений/Сдвиг по фазеСкачать

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) — схема цепи; б) — сдвиг фаз тока и напряжения; в) — треугольник напряжений; д) — треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z 2 ) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

Извлекая квадратный корень из обеих частей этого равенства, получим,

Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) — схема цепи; б) — треугольник сопротивлений .
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) — схема цепи; б) — треугольник сопротивлений .
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.


Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Видео:Откуда взялась формула полного сопротивления цепи? Треугольник напряжений, треугольник сопротивленийСкачать
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C .
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

Приводя к общему знаменателю подкоренное выражение, получим:


Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:

Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

При соблюдении этого условия полное сопротивление колебательного контура будет равно:

где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Треугольник сопротивлений
Автор: Евгений Живоглядов.
Дата публикации: 01 апреля 2015 .
Категория: Статьи.
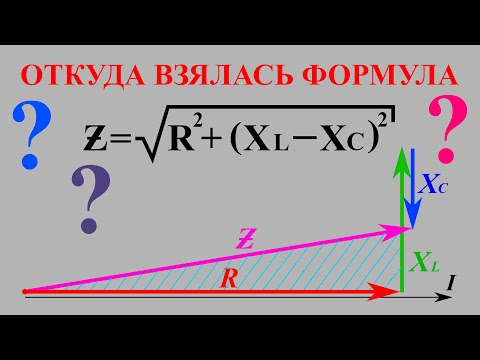
Если стороны треугольника напряжений (рисунок 1, а) разделить на ток I (рисунок 1, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому – треугольник сопротивлений (рисунок 1, в).
Рисунок 1. Получение треугольника сопротивлений
В треугольнике сопротивления, показанном отдельно на рисунке 2, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.
Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного xL сопротивлений.
Применяя теорему Пифагора к треугольнику сопротивлений, получаем:
Если одно из сопротивлений цепи (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко можно убедиться непосредственным расчетом.
Пример 1. Определить полное сопротивление цепи, в которой r = 9 Ом и xL = 12 Ом.
Было бы совершенно неправильно, если бы для определенного полного сопротивления были арифметически сложены оба сопротивления r и xL, так как
Результат, как мы видим, в этом случае получается неверный.
Пример 2. Полное сопротивление обмотки электромагнита z = 25 Ом. Активное сопротивление обмотки r = 15 Ом. Определить индуктивное сопротивление.
Пример 3. Индуктивное сопротивление обмотки электродвигателя переменного тока равно 14 Ом. Полное сопротивление ее равно 22 Ом. Найти активное сопротивление.
Пример 4. В цепи, изображенной на рисунке 3, определить показание вольтметра.
Рисунок 3. К примеру 4
Определим общее сопротивление:
Если умножить z на ток I, получим:
то есть тот же результат, что и выше.
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
Видео:Соединение обмоток треугольникомСкачать

Треугольник сопротивлений
Активное сопротивление
В цепи действия напряжения и тока, создает противодействие, снижения напряжения на активном сопротивлении. Падение напряжения, созданное током и оказывающее противодействие ему, равно активному сопротивлению. При протекании тока по компонентам с активным сопротивлением, снижение мощности становится необратимым. Отличительным признаком элементов цепи, которые обладают только активной составляющей сопротивления, является совпадение напряжения и тока по фазе. Это сопротивление вычисляется по формуле:
R = U/I, где R – сопротивление элемента, U – напряжение на нем, I – сила тока, протекающего через элемент цепи.
На активное сопротивление влияют свойства и параметры проводника: температура, поперечное сечение, материал, длина.
Реактивное сопротивление
Тип сопротивления, определяющий соотношение напряжения и тока на емкостной и индуктивной нагрузке, не обусловленное количеством израсходованной электроэнергии, называется реактивным сопротивлением. Оно имеет место только при переменном токе, и может иметь отрицательное и положительное значение, в зависимости от направления сдвига фаз тока и напряжения. При отставании тока от напряжения величина реактивной составляющей сопротивления имеет положительное значение, а если отстает напряжение от тока, то реактивное сопротивление имеет знак минус.
Треугольник сопротивлений
Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.
Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.
По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.
7. Активное сопротивление расходует потребляемую мощность практически только на нагрев самого себя, ток через него совпадает по фазе с напряжением, приложенным к нему. Реактивное сопротивление может запасать энергию, ток через него в зависимости от характера (емкостное или индуктивное) будет или опережать или отставать по фазе от приложенного напряжения.
8. Сопротивление, оказываемое переменному току ЭДС самоиндукции, носит название индуктивного сопротивления.
Индуктивное сопротивление будет тем больше, чем больше индуктивность потребителя (цепи) и выше частота переменного тока. Это сопротивление выражается формулой xl = ωL, где xl — индуктивное сопротивление в омах; L — индуктивность в генри (гн); ω — угловая частота где f — частота тока).
Кроме индуктивного сопротивления существует емкостное сопротивление, обусловливаемое как наличием емкости в проводниках и обмотках, так и включением в отдельных случаях в цепь переменного тока конденсаторов. При увеличении емкости С потребителя (цепи) и угловой частоты тока емкостное сопротивление уменьшается.
Емкостное сопротивление равно xс = 1/ωС, где хс — емкостное сопротивление в омах, ω — угловая частота, С — емкость потребителя в фарадах.
9. Цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
10. Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.
Действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
📸 Видео
Звезда,треугольник соединение сопротивленийСкачать
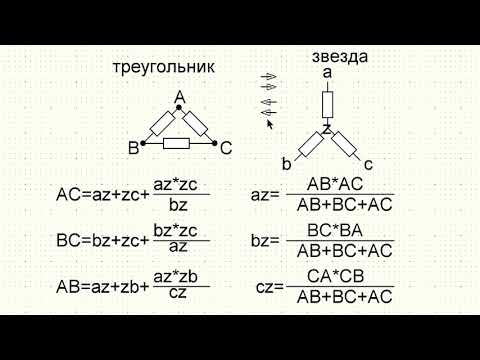
Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Соединение треугольникомСкачать

Что такое звезда и треугольник в трансформаторе?Скачать

Лекция 24. Преобразование треугольника в звезду.Скачать

Что такое ИМПЕДАНС | РЕАКТИВНОЕ СОПРОТИВЛЕНИЕСкачать
Трехфазные электрические цепи │Теория ч. 1Скачать

Треугольник в звезду и наоборот.Скачать
Мощность трехфазного напряжении при подключении нагрузки звездой и треугольникомСкачать

Лекция 25. Преобразование звезды в треугольник.Скачать

Принцип работы трансформатораСкачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Лекция по электротехнике 4.1 - Двухполюсник. Треугольники сопротивлений и проводимостейСкачать