| Название | Лабораторные и практические работы по методике преподавания математики |
| Анкор | Е.И. Лященко ЛАБ и ПРАКТ РАБОТЫ ПО МПМ.doc |
| Дата | 02.02.2017 |
| Размер | 3.28 Mb. |
| Формат файла |  |
| Имя файла | Е.И. Лященко ЛАБ и ПРАКТ РАБОТЫ ПО МПМ.doc |
| Тип | Документы #1765 |
| страница | 6 из 18 |
| Подборка по базе: формы и методы поиска работы памятка для студентов.docx, Научные и практические достижения медицинской микробиологии.docx, ЭиТОПС. Лабораторная работа №1. Порядок работы.rtf, Задание для работы в Word.pdf, Титульный лист для практической работы (1).docx, ЛАБОРАТОРНЫЕ РАБОТЫ.docx, Пример курсовой работы.docx, Титульный лист для практической работы.docx, Лабораторные работы CS3202 Цифровая схемотехника_каз (1).docx, Информатика, Практические задания.docx Разъяснительная часть: «n — любое натуральное число». Утверждение сформулировано в импликативной форме. Отмечается, что так как в утверждении одно условие и одно заключение, то утверждение простое. Используя логические символы, утверждение можно записать так:
Результат анализа можно оформить в виде таблицы (табл. 5). Таблица 5 (кодопозитив)
Задание 2. Выполните логико-математический анализ утверждения Вертикальные углы равны, ответив на вопросы:
Задание 3. Выполните логико-математический анализ теоремы 3.6 [113]. Краткая запись теоремы может быть такой: Теорема сформулирована в импликативной форме. Разъяснительная часть: теорема рассматривается на множестве любых пар треугольников АВС и Условие: Сколько условий? (Три.) Какая связь между условиями? (Соединены союзом «и».) Заключение: Сколько заключений? (Одно.) Так как в теореме три условия, то теорема сложная. Задание 4. Заполните таблицу (см. табл. 6) логико-математического анализа теоремы 3.5 [113]. Теорема сформулирована в категорической форме. Таблица 6 (кодопозитив)
Примечание. Союз «и» в формулировке теоремы употребляется в соединительном смысле. 3адание 5. Может ли сложная теорема иметь одновременно несколько условий и несколько заключений? Из школьного учебника геометрии приведите пример такой теоремы. Задание 6. Сформулируйте утверждение, обратное данному. (Надо оставить без изменения разъяснительную часть, а условие и заключение поменять местами.) Например, для утверждения
обратным будет утверждение
Сформулируйте утверждение, обратное следующему: Вертикальные углы равны. Будет ли сформулированное утверждение теоремой? Почему? 3адание 7. Как получить утверждение, противоположное данному? (Если оставить без изменения разъяснительную часть, а условие и заключение утверждения заменить их отрицаниями, то получим утверждение, противоположное данному.) противоположным будет утверждение Вертикальные углы равны. Будет ли это утверждение теоремой? Сформулируйте утверждения, противоположные теоремам 3.5 и 3.6 [113]. Являются ли эти утверждения теоремами? 3адание 8. Какое получим утверждение: обратное противоположному или противоположное обратному, если оставить без изменения разъяснительную часть и поменять местами условие и заключение утверждения, противоположного данному?
будет обратным противоположному или противоположным обратному? Сформулируйте для утверждения Вертикальные углы равны утверждение, обратное противоположному. Является ли сформулированное утверждение теоремой? Почему? Сформулируйте утверждения, обратные противоположным для теорем 3.5 и 3.6 [113]. Будут ли они теоремами? 3адание 9. На основании рассмотренных примеров сделайте вывод о взаимосвязи между прямым, обратным, противоположным и обратным противоположному утверждениями. Какие из них одновременно являются теоремами? Общие приемы работы с теоремой. При индуктивном введении теоремы можно условно выделить следующие этапы ее изучения:
Для мотивировки необходимости изучения теорем можно предложить такие приемы: Прием 1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык. Мотивировать необходимость изучения свойства Две различные прямые либо не пересекаются, либо пересекаются только в одной точке можно, предложив предварительно учащимся решить дома следующие задачи: а) На плане местности четыре населенных пункта отмечены точками А, В,С, К. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта К в пункт В (рис. 2, пути считаем прямолинейными). Если пересекутся, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересечься в двух точках? В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо не имеют ни одной. Отметив, что пути движения в данных задачах были отрезками, предлагается подумать над вопросом: изменится ли вывод, если вместо двух отрезков взять две прямые? Ответы могут быть разными. Если ответы разные, то сразу можно предложить выяснить, могут ли две прямые иметь две общие точки, и тем самым перейти к доказательству теоремы, мотив изучения которой стал очевидным. Если же ответ один, т. е. две различные прямые пересекаются в одной точке, то учитель говорит, что в этой задаче это действительно так. При решении других задач может быть по-другому: ведь мы не можем рассмотреть все конкретные жизненные ситуации и прорешать все задачи! Как быть?
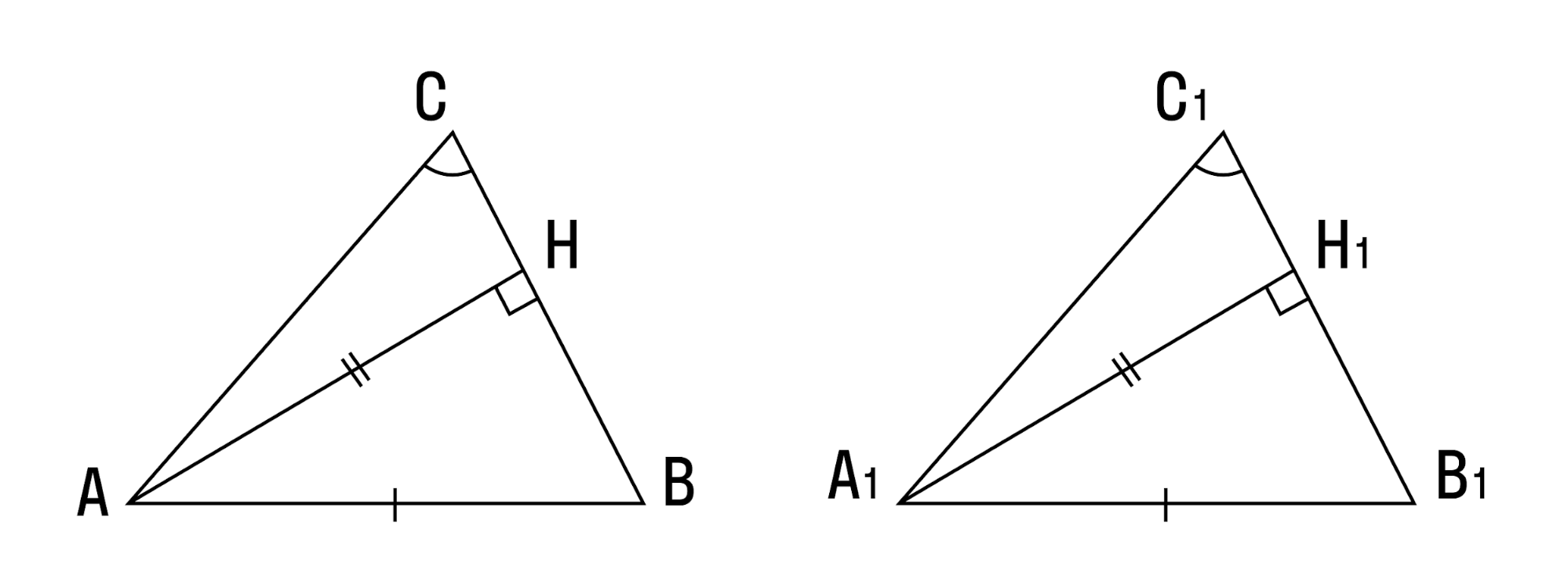
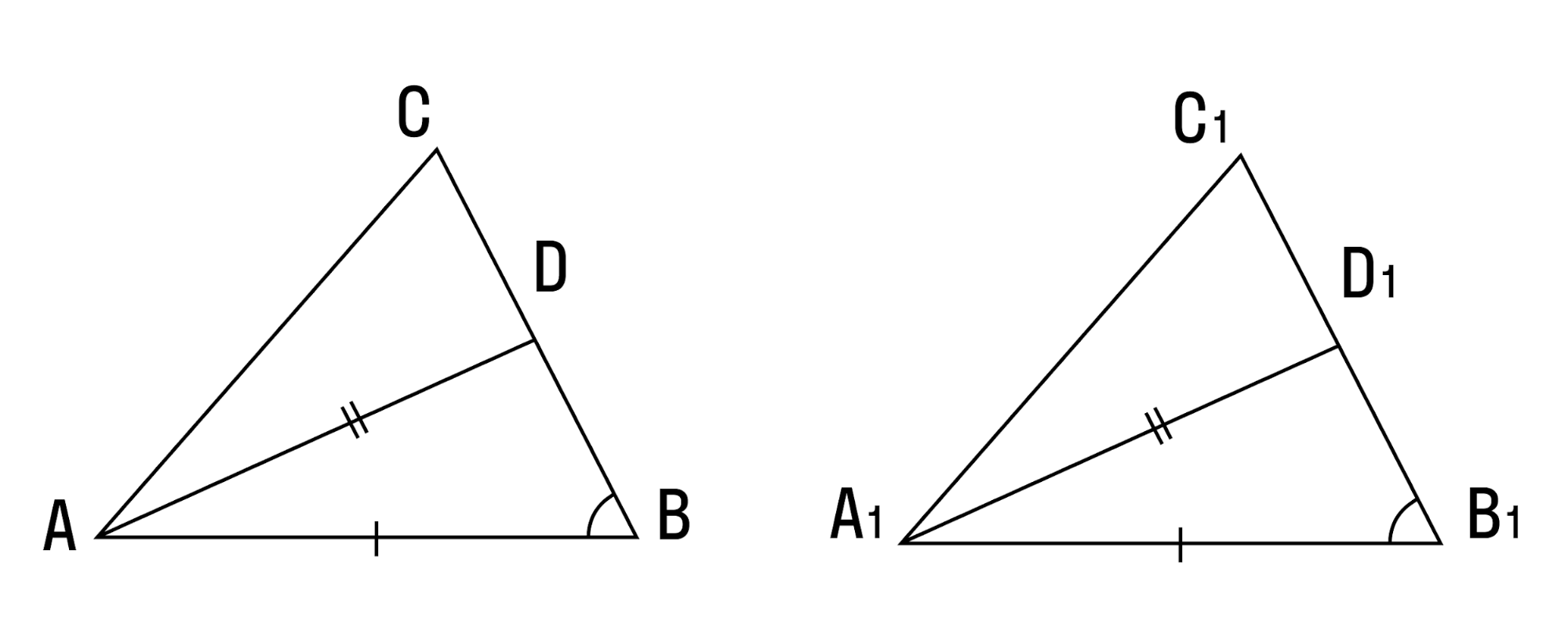
Этот прием можно использовать при изучении многих теорем. 3адание 10. Подберите или составьте задачи, с помощью которых можно мотивировать изучение теорем 1.2, 2.3, 4.4 [113]. Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач. Для мотивации изучения теоремы Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны можно использовать следующую задачу: К Картографы считают, что расстояние DM равно расстоянию АВ (в соответствующем масштабе). Правы ли картографы?
Мотив изучения и необходимость доказательства теоремы показаны. Задание 11. Подберите подходящую практическую задачу для мотивации изучения теоремы. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем. Например, перед доказательством теоремы 3.3 [113] учащимся предлагается решить задачу: В равнобедренном треугольнике АВС (АВ=BС)вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников? Так как третьего признака равенства треугольников по трем сторонам (теорема 3.6) у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем 3.3, 3.5, 3.6 [113]. Задание 12. Покажите, как, осуществляя поиск решения сформулированной выше задачи, можно мотивировать изучение теорем 3.3, 3.5, 3.6. (Задание выполняется группами по 3-5 человек.) Прием 4. Показ, как решалась данная проблема в истории науки. Задание 13. Подберите пример. где бы использовался этот прием мотивации изучения теорем. Очевидно, что перечисленные выше приемы для мотивации изучения теорем служат одновременно и раскрытию содержания теоремы. Из других приемов раскрытия содержания теорем можно назвать:
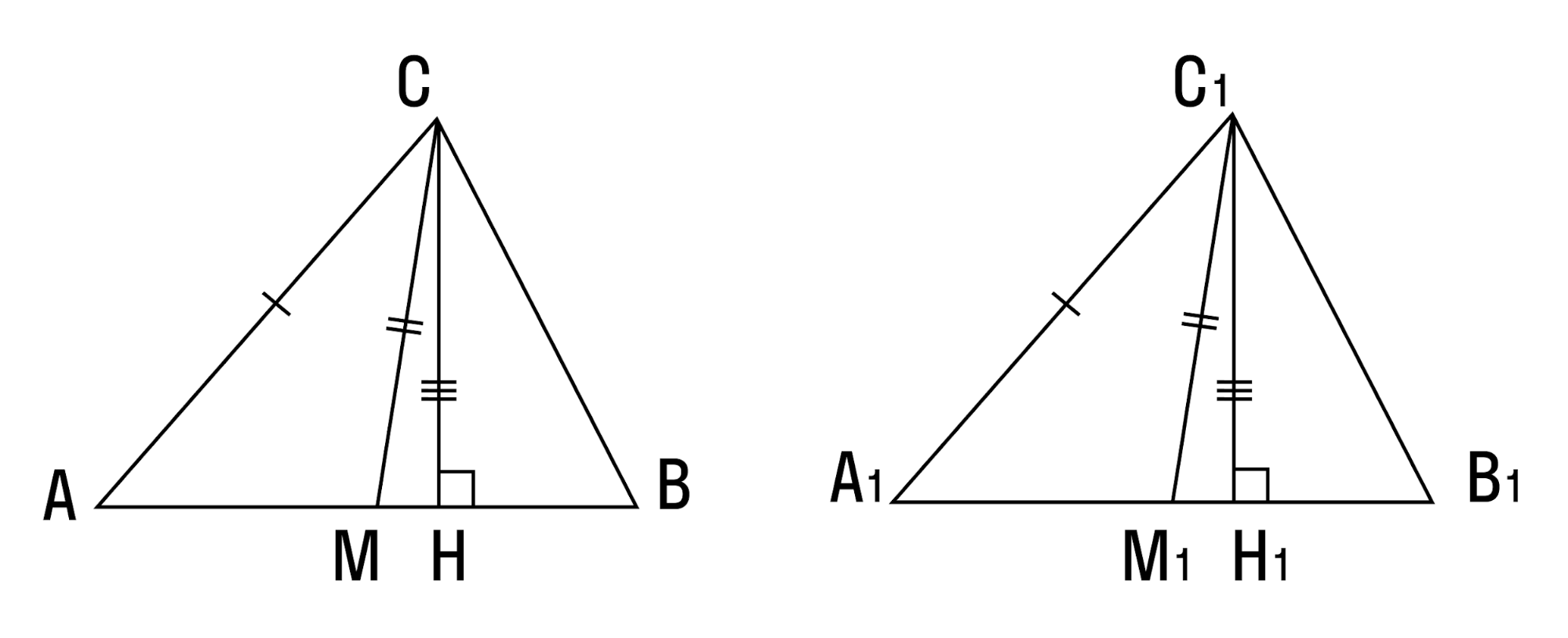
Приводятся примеры. Пример 1. Чтобы раскрыть содержание теоремы 2.4, учащимся предлагается в тетрадях (чтобы потом можно было использовать чертеж и для дальнейшей работы) начертить полупрямую а,отложить от полупрямой а в одну полуплоскость Несмотря на то что все брали разные углы (но у всех Пример 2. Для раскрытия содержания теоремы Фалеса (теорема 6.6) можно использовать следующий прием: начертить в тетрадях угол (произвольный) (на доске это делает учитель); отложить на одной стороне угла последовательно несколько равных отрезков; через концы отрезков провести параллельные прямые до пересечения со второй стороной угла; измерить отрезки, получившиеся на второй стороне угла, и сравнить их между собой. После этой работы высказывается предположение (формулируется теорема), которое затем доказывается. Пример 3. Раскрыть содержание теоремы 6.4 можно, решив с учащимися устно несколько задач вида «Вычислите диагонали прямоугольника АВСК,если его стороны равны: а) 3 и 4 см; б) 6 и 8 дм; в) 12 и 9 м». Какой вывод можно сделать из решения этих задач? Задание 14. Покажите возможные приемы раскрытия содержания теорем 4.4, 4.5, 6.1. Образец записи доказательства теоремы на примере теоремы 3.5 (табл. 7): Т BK — медиана, проведенная к основанию. 1. BK — биссектриса, Можно составить структурную схему доказательства. Приведем такую схему для случая (1) (кодопозитив): О С Чтобы теорема была усвоена, необходима работа с ней и после ее доказательства. Этому способствуют задания следующих видов:
При этом предлагаются задачи на применение только что изученной теоремы: задачи на распознавание фигур или взаимного положения элементов фигур на чертежах, к которым можно применить теорему, причем решение задачи в этом случае до конца можно и не доводить; задачи, для решения которых используется изученная теорема наряду с другими, ранее изученными. Само собой разумеется, что эта работа проводится не только на одном-двух уроках, когда изучается та или иная теорема, а по мере возможности проводится и при изучении других вопросов. Проследим все этапы работы над теоремой на примере теоремы: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. I этап. Один из приемов мотивации изучения этой теоремы — знание теоремы для решения задач. Можно использовать другой. прием, показав конструкцию строительной фермы (рис. 4), где АС=СВ, AD=DB, DM=MB;простейшую конструкцию стропил (рис. 5) АВ=ВС и АК=КС, т.е. наблюдение жизненных фактов. С целью мотивации изучения этой теоремы можно использовать решение практической задачи. Ч Можно использовать решение учебно-практической задачи: Чтобы разделить угол Р пополам с помощью только масштабной линейки, поступают так: 1) откладывают на сторонах угла Р (рис. 7) равные отрезки РМ и РК; 2) соединяют точки М и К отрезком; 3) делят отрезок МК пополам, получают точку В; 4) проводят луч РВ. РВ — искомая биссектриса, разделившая угол пополам. Почему? II этап. Чтобы учащиеся «открыли» сами содержание теоремы и сформулировали ее, проводится такая практическая работа. Перед уроком дается на дом задание: начертить три равнобедренных треугольника (остроугольный разносторонний, прямоугольный и тупоугольный) и в этих треугольниках построить медианы и высоты к боковым сторонам (с помощью масштабной линейки и угольника), биссектрисы углов при основании (с помощью транспортира). А на уроке предлагается по вариантам выполнить другую практическую работу: начертить в тетрадях равнобедренный треугольник и построить медиану и высоту к основанию и биссектрису угла при вершине, противолежащей основанию. Трое учащихся (по одному от каждого варианта) выполняют эту работу на доске. Учитель тем временем может построить разносторонний треугольник и провести в нем медианы, высоты и биссектрисы (этот рисунок можно заготовить заранее). После выполнения практической работы обсуждаются ее результаты. У учащихся в каждом из данных случаев медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой. Ставятся вопросы: обладает ли этим свойством медиана, проведенная из вершин двух других углов равнобедренного треугольника к противолежащей стороне) Нет. Это видно из рисунков, выполненных в домашней практической работе. Обладают ли этим свойством медианы, проведенные в разностороннем треугольнике? Нет. Учитель демонстрирует свой рисунок. Итак, практическим путем установлен новый факт. Какой? Учащиеся формулируют теорему. Если есть необходимость, учитель уточняет их ответы. III этап. Мотивируется необходимость доказательства теоремы. Перед учащимися ставится вопрос: во всех ли равнобедренных треугольниках медиана, проведенная к основанию, является биссектрисой и высотой? — Неизвестно. В тех, которые рассматривались, да. А в других — неизвестно. Как быть? Делается вывод о том, что необходимо доказать справедливость теоремы для любого равнобедренного треугольника. IV этап. Проводится работа над структурой теоремы: выделяется условие, заключение, еще раз уточняется, что теорема сформулирована для равнобедренного треугольника. На доске и в тетрадях выполняется чертеж, записывается, что дано и что требуется доказать (см. табл. 7). V этап. Поиск доказательства осуществляется движением от заключения к условию, т.е. аналитически (см. с. 194-200). Записывается доказательство (см. табл. 7). Работа по закреплению теоремы VI этап. Усвоение формулировки теоремы. 1) Верно ли сформулирована теорема: «Медиана, проведенная к основанию, является биссектрисой и высотой»? Почему? 2) Вставьте пропущенные слова: «В . треугольнике медиана, проведенная . является . и . ». Текст проецируется через кодоскоп. 3) Сформулируйте теорему со словами: «Если . , то . ». VII этап. Усвоение доказательства теоремы.
VIII этап. Решение задач на применение теоремы. 1) Точка M принадлежит высоте равнобедренного треугольника, проведенной к основанию. Принадлежит ли эта точка: а) биссектрисе угла при вершине? б) медиане, проведенной к основанию? Почему? 2) Точка Р принадлежит биссектрисе угла треугольника. Принадлежит ли эта точка высоте треугольника? Почему? 3) Можно ли с помощью только масштабной линейки построить биссектрису угла при вершине равнобедренного треугольника? Высоту? Дайте обоснование ответа. 4) Длина медианы равнобедренного треугольника, проведенной к основанию, равна 10 см. Чему равны длины биссектрисы и высоты, проведенных из той же вершины? 5) Докажите, что в равностороннем треугольнике биссектриса каждого из углов является медианой и высотой, проведенными из вершины угла к противоположной стороне. Будут ли равны все биссектрисы, медианы и высоты между собой? Предлагается решить более сложные задачи, например № 23, 27, 29 и др. [113]. 1. Выполните логико-математический анализ теоремы: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны». 2. Для этой теоремы сформулируйте утверждения: обратное, противоположное и противоположное обратному. 3. Выделите основные этапы работы с данной теоремой в классе. Литература: [125], [93], [32], [52], [l6], [17], [18], [44], [45], [46]. Содержание
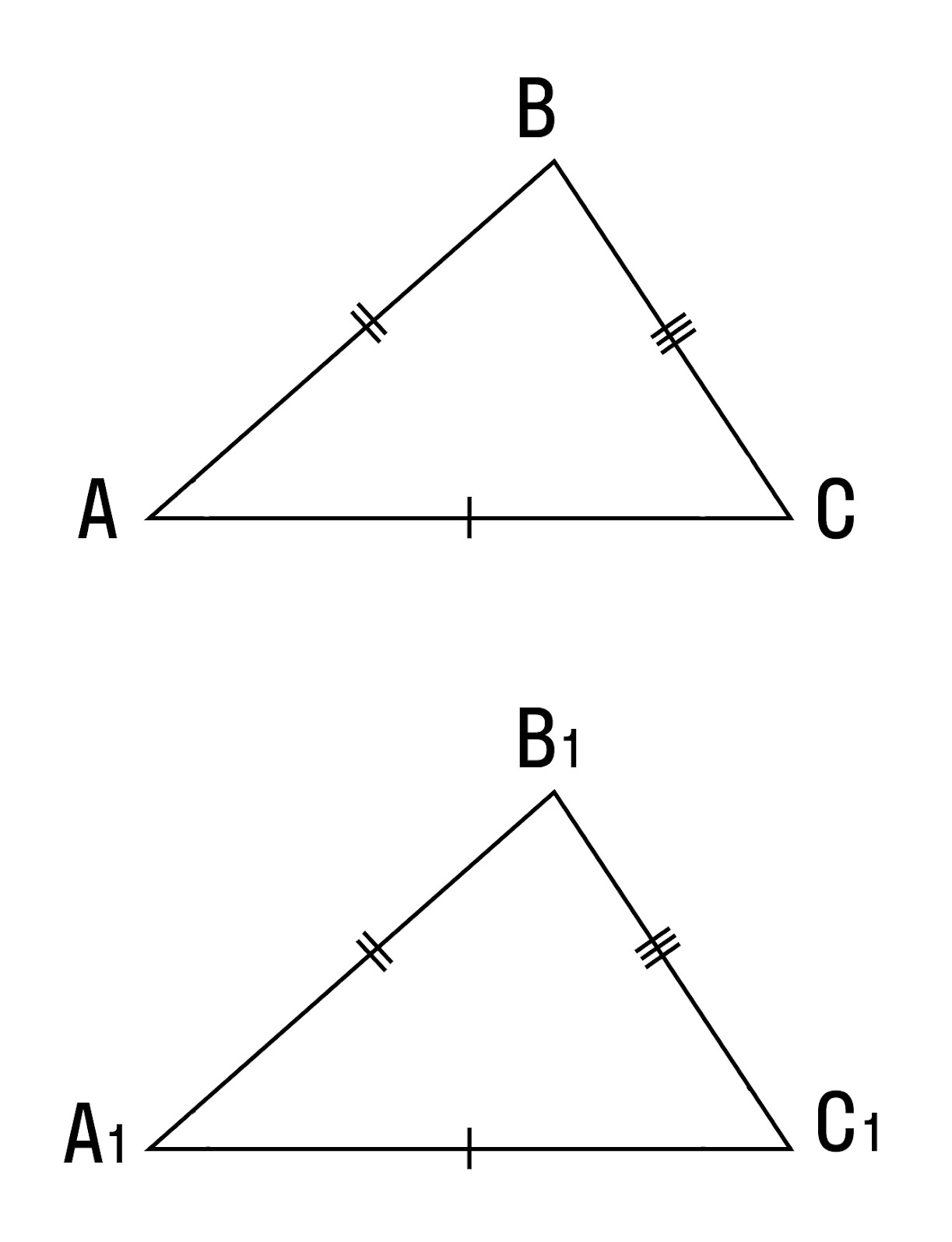
Видео:Первый признак равенства треугольников. 7 класс.Скачать  Признаки равенства треугольниковО чем эта статья: Видео:Признаки равенства треугольников. 7 класс.Скачать  Первый признак равенства треугольниковКонечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать. Давайте рассмотрим три признака равенства треугольников. Теорема 1. Равенство треугольников по двум сторонам и углу между ними. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1. Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1. Значит, происходит совмещение вершин В и В1, С и С1. Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать  Второй признак равенства треугольниковТеорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1. Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1. AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1. CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1. Вершина B совпадает с вершиной B1. Видео:Второй признак равенства треугольников. 7 класс.Скачать  Третий признак равенства треугольниковТеорема 3. Равенство треугольников по трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Доказательство 3 признака равенства треугольников: Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1. Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников. Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
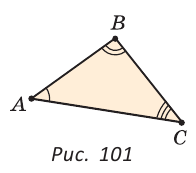
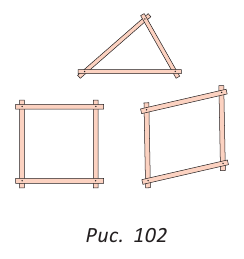
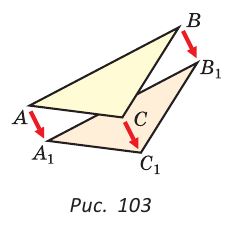
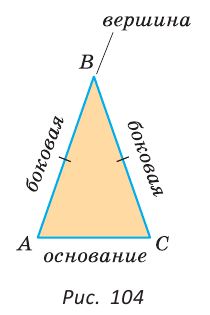
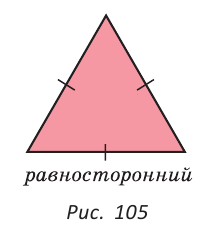
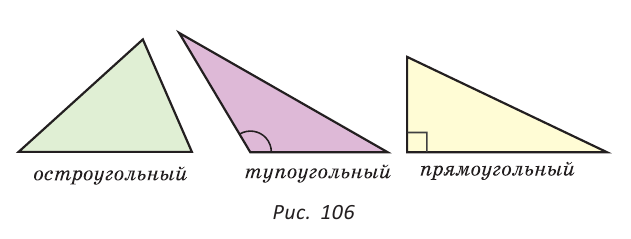
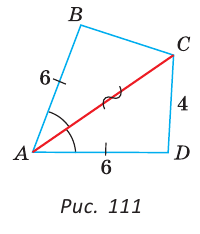
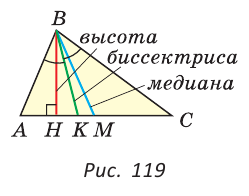
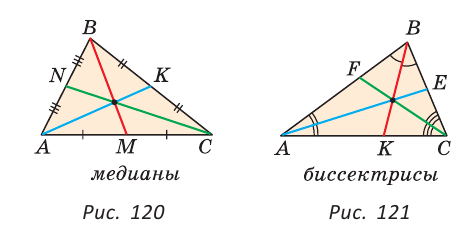
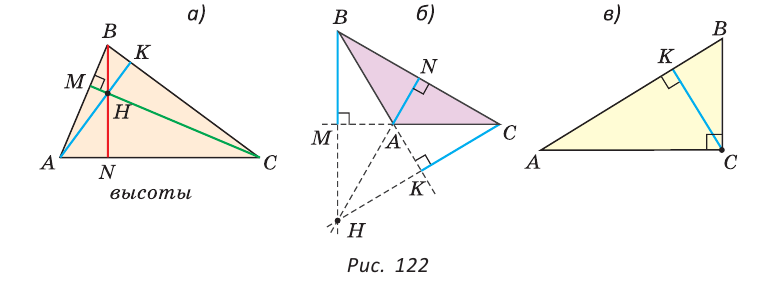
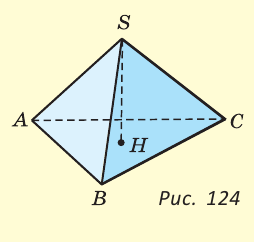
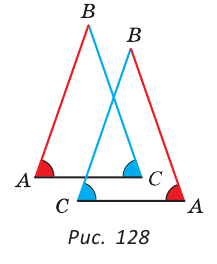
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура. Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать  Признаки равенства треугольников — определение и вычисление с примерами решенияСодержание: Если на плоскости отметить три точки А, В и С, не лежащие на одной прямой, и соединить их отрезками, то получим треугольник ABC. Можно сказать, что треугольник — это трехзвенная замкнутая ломаная. Обозначают: Видео:Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать 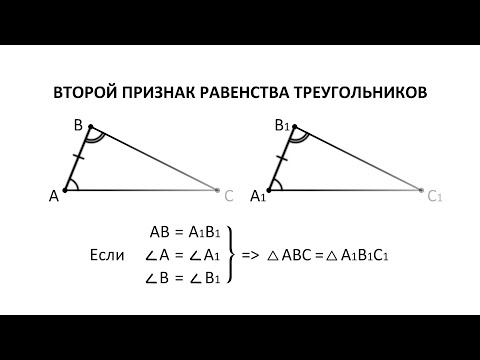 ОпределенияОпределение. Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Если соединить концами три деревянных планки, то получится треугольник, который нельзя подвергнуть деформации — он будет сохранять свою форму. Тогда как четырехугольник может менять свою форму (рис. 102)? Это свойство «жесткости» треугольника широко используется в технике, производстве, строительстве. Равные треугольникиРавные треугольники можно совместить наложением так, что соответственно совпадут все три стороны и все три угла (рис. 103). В совпавших, то есть в равных треугольниках, против равных сторон лежат равные углы, а против равных углов — равные стороны. Если Для совмещения равных отрезков достаточно совпадения их концов, а для совмещения равных треугольников — совпадения их вершин. Виды треугольниковЕсли у треугольника все три стороны имеют разную длину, то такой треугольник называется разносторонним. Треугольник, у которого две стороны равны, называется равнобедренным. Его равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника (рис. 104). Если у треугольника равны все три стороны, то он называется равносторонним (рис. 105). Равносторонний треугольник является также и равнобедренным, где любую пару сторон можно принять за боковые стороны. По величине углов треугольники делятся на остроугольные (у них все углы острые), тупоугольные (есть тупой угол) и прямоугольные (есть прямой угол) (рис. 106). Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Периметром треугольника (многоугольника) называется сумма длин его сторон. Равными треугольниками называются треугольники, которые можно совместить наложением. Равнобедренным треугольником называется треугольник, у которого две стороны равны. Равносторонним треугольником называется треугольник, у которого все стороны равны. Свойство равных треугольников. В равных треугольниках против равных сторон лежат равные углы, а против равных углов — равные стороны. Замечание. Называя или записывая равные треугольники, стараются соблюдать последовательность соответствующих вершин. Во многих случаях это удобно. Однако делать это необязательно. Обе записи: Первый и второй признаки равенства треугольниковПри выяснении равны ли треугольники нет необходимости устанавливать равенство всех их соответствующих элементов путем наложения или измерения. Следующие две теоремы гарантируют равенство треугольников при равенстве некоторых сторон и углов. Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Дано: АВ =А1В1, АС =А1С1, Доказать: Доказательство: Наложим треугольник ABC на треугольник А1В1С1 так, чтобы совпали равные углы А и А1, луч АВ совпал с лучом А1В1, а луч АС совпал с лучом А1С1. Так как отрезки АВ и А1В1 равны, то они совпадут при наложении, и вершина В совпадет с вершиной В1. Аналогично совпадут равные отрезки АС и A1C1, вершина С совпадет с вершиной C1. Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, Говорят, что две стороны и угол между ними задают треугольник однозначно. Теорема (второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. AC =А1С1, Доказать: Доказательство: Наложим треугольник ABC на треугольник А1В1С1 так, чтобы совпали равные стороны АС и А1С1, угол А совпал с равным углом А1, а угол С — с равным углом Сх. Тогда луч АВ совпадет с лучом А1В1, луч СВ — с лучом С1В1, а вершина В совпадет с вершиной В1 (точка В будет принадлежать и прямой Говорят, что сторона и два прилежащих к ней угла задают треугольник однозначно Пример №1Отрезки АВ и CD пересекаются в их серединах. Доказать, что расстояния между точками А и С, В и D равны. Доказательство: Пусть О — точка пересечения отрезков АВ и CD (рис. 110). Рассмотрим Возможно краткое оформление решения задачи. Пример №2Дана простая замкнутая ломаная ABCD, у которой АВ =AD = 6 см, CD -4 см и луч АС является биссектрисой угла BAD. Найти длину ломаной ABCD. Решение: У треугольников ABC и ADC сторона АС — общая (рис. 111), AB=AD по условию, Эти треугольники равны по 1-му признаку равенства треугольников. Отсюда ВС = CD как соответствующие (соответственные) стороны в двух равных треугольниках. Длина ломаной ABCD: Пример №3На сторонах угла В отложены отрезки: ВА = ВС, КА-МС (рис. 112). Доказать, что Доказательство: Рассмотрим треугольники АВМ и СВК. У них Пример №4На рисунке 113 Доказательство: Так как Так как Высота, медиана и биссектриса треугольникаУ треугольника, помимо трех сторон, трех вершин и трех углов, имеются также и другие элементы — высота, медиана и биссектриса. Определение. Высотой треугольника (рис. 118, а) называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на ее продолжение (отрезок ВН). Определение. Медианой треугольника (рис. 118, б) называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны (отрезок ВМ). Определение. Биссектрисой треугольника (рис. 118, в) называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения биссектрисы с противоположной стороной (отрезок ВК). В равных треугольниках равны соответствующие высоты, медианы и биссектрисы. Если треугольник не равнобедренный, то высота, медиана и биссектриса, проведенные из одной вершины треугольника, не совпадают (рис. 119). Поскольку у треугольника три вершины, то у него и три высоты, три медианы, три биссектрисы. Позже мы докажем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Это же касается медиан треугольника (рис. 120) и его биссектрис (рис. 121). Если треугольник остроугольный (рис. 122, а), то точка пересечения его высот находится внутри треугольника ABC. Если треугольник тупоугольный или прямоугольный (рис. 122, б, в), то продолжения высот пересекаются соответственно вне треугольника или в вершине прямого угла. Точки пересечения высот, биссектрис и медиан называются замечательными точками треугольника. Геометрия 3D Тетраэдром или треугольной пирамидой называется многогранник, у которого все четыре грани — треугольники. Любую его грань можно принять за основание, а противолежащую вершину — за вершину пирамиды. Если точка S — вершина, а треугольник ABC — основание пирамиды, то перпендикуляр SH к плоскости ABC является высотой тетраэдра (рис. 124). Равнобедренный треугольникОпределение. Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника. Рассмотрим некоторые свойства равнобедренного треугольника и один из его признаков. Теорема (о свойстве углов при основании). В равнобедренном треугольнике углы при основании равны. Дано: Доказать: Доказательство: Проведем биссектрису ВК треугольника ABC. Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК — общая, АВ = ВС по условию, углы АВК и СВК равны по определению биссектрисы. Из равенства этих треугольников следует, что Теорема (о свойстве биссектрисы равнобедренного треугольника). В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой. Дано: Доказать: ВК — медиана и высота. Доказательство: Треугольники АВК и СВК равны по двум сторонам и углу между ними (см. предыдущую теорему). Из равенства треугольников следует, что АК=КС и Замечание. Поскольку из вершины треугольника можно провести только одну биссектрису, одну высоту и одну медиану, то теорему можно сформулировать так: «Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают». То есть если по условию задачи дана высота равнобедренного треугольника, проведенная к основанию, то согласно данной теореме она является биссектрисой и медианой. Аналогично, если дана медиана равнобедренного треугольника, проведенная к основанию, то она является высотой и биссектрисой. Теорема (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный. Дано: Доказать: Доказательство: Мысленно перевернем треугольник ABC обратной стороной (рис. 128) и наложим перевернутый треугольник на треугольник ABC так, чтобы их стороны АС совпали, угол С совпал с углом А, угол А совпал с углом С. Тогда перевернутый треугольник совместится с данным, и сторона ВС совместится со стороной АВ. Следовательно, АВ = ВС, т. е. Доказанный признак равнобедренного треугольника является теоремой, обратной теореме о свойстве углов при основании равнобедренного треугольника (рис. 129). Напомним, что любая теорема состоит из условия — того, что дано, и заключения — того, что нужно доказать. У теоремы, обратной данной, условием является заключение данной теоремы, а заключением — условие данной. Пример №5Доказать, что в равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой. Доказательство: Пусть в Замечание. Вторым способом доказательства будет рассмотрение Пример №6Доказать, что перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду пополам. Доказательство: Пусть О — центр окружности, АВ — хорда, ОН — перпендикуляр к хорде АВ (рис. 131). Отрезки OA и ОВ равны как радиусы. Поэтому треугольник АОВ — равнобедренный, а ОН — его высота, проведенная к основанию. Мы знаем, что высота равнобедренного треугольника, проведенная к основанию, является и медианой. А медиана делит сторону треугольника пополам, то есть АН = НВ. Что и требовалось доказать. Признаки равнобедренного треугольникаВы уже знаете один признак равнобедренного треугольника: «Если в треугольнике два угла равны, то треугольник равнобедренный». Докажем еще три признака равнобедренного треугольника, связанных с его высотой, медианой и биссектрисой. Теорема. Если в треугольнике высота является медианой, то треугольник равнобедренный. Дано: ВН — высота и медиана Доказательство: Рассмотрим Теорема. Если в треугольнике высота является биссектрисой, то треугольник равнобедренный. Дано: ВН — высота и биссектриса Доказать: АВ = ВС (рис. 137). Доказательство: Рассмотрим Теорема. Если в треугольнике медиана является биссектрисой, то треугольник равнобедренный. Дано: ВМ — медиана и биссектриса Доказать: АВ = ВС (рис. 138). Доказательство: Продлим медиану ВМ на ее длину за точку М. Получим МВХ = ВМ. Треугольники АМВ1 и СМВ равны по двум сторонам и углу между ними (МВ1 = ВМ по построению; AM = МС, так как ВМ — медиана; Замечание. Прием продления (продолжения) медианы часто используется при решении геометрических задач. Пример №7В треугольнике ABC с периметром 54 см медиана АК перпендикулярна стороне ВС, а высота ВМ составляет равные углы со сторонами ВА и ВС. Найти стороны треугольника ABC. Решение: Так как медиана АК является и высотой, то Пример №8Биссектриса АК треугольника АБС делит сторону ВС пополам. Периметр треугольника ABC равен 36 см, периметр треугольника АКС равен 30 см. Найти длину биссектрисы АК. Решение: Из условия следует, что биссектриса АК является и медианой Тогда Геометрия 3D У правильной треугольной пирамиды DABC в основании лежит равносторонний треугольник ABC, а боковые грани ADB, ADC, BDC — равные равнобедренные треугольники с общей вершиной D (рис. 142). У правильной четырехугольной пирамиды в основании лежит квадрат MNKE, а боковые грани МРЕ, MPN, NPK, ЕРК — равные равнобедренные треугольники с общей вершиной Р (рис. 143). Третий признак равенства треугольниковВам уже известны два признака равенства треугольников. Рассмотрим еще один. Теорема (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Доказать: Доказательство: Приложим треугольник А1В1С1 к треугольнику ABC так, чтобы у них совместились равные стороны А1С1 и АС, а вершины В1 и В оказались в разных полуплоскостях относительно прямой АС. Треугольник А1В1С1 займет положение треугольника АВ2С. Проведем отрезок ВВ2. Так как АВ2=АВ и В2С = ВС, то треугольники АВВ2 и СВВ2 — равнобедренные. Откуда Замечание. Чтобы отрезок ВВ2 проходил внутри треугольника ABC, следует прикладывать треугольники большей стороной. Говорят, что три стороны задают треугольник однозначно. Итак, теперь вы знаете три признака равенства треугольников. Можно сформулировать и другие признаки равенства треугольников, в которых неизбежно будет присутствовать соответственное равенство каких-то трех элементов двух треугольников. Однако не любые три элемента задают треугольник. Так, например, если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники не обязательно равны. То же касается треугольников, у которых соответственно равны две стороны и угол, противолежащий одной из этих сторон. На рисунке 145, а, б вы видите пары таких неравных треугольников. Пример №9У простой замкнутой ломаной ABCD AB=AD, BC = DC. Доказать, что Доказательство: Проведем отрезок АС (рис. 146). Треугольники ABC и ADC равны по 3-му признаку равенства треугольников (AB=AD и BC = DC по условию, сторона АС — общая). Поэтому Пример №10Доказать равенство треугольников по двум сторонам и медиане между ними. Доказательство: Нужно доказать, что Пример №11Два равных отрезка АВ и CD пересекаются в точке О и AD = BC. Доказать, что ВО = DO. Доказательство: Соединим точки В и D отрезком (рис. 148). Треугольники ABD и CDB равны по трем сторонам (сторона BD — общая, AB=CD и AD=СВ по условию). Из равенства треугольников следует, что Серединный перпендикуляр к отрезкуОпределение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину. Прямая CD — серединный перпендикуляр к отрезку АВ, то есть
Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку. В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно. 1) Дано: Доказательство: По определению серединного перпендикуляра 2) Дано: Доказать: Доказательство: Проведем в равнобедренном Геометрическим местом точек плоскости (или пространства) называется множество всех точек плоскости (или пространства), обладающих общим свойством. Из доказанной теоремы следует, что серединный перпендикуляр к отрезку — это геометрическое место точек плоскости, равноудаленных от концов отрезка. Пример №12В четырехугольнике (рис. 155) ABCD AB=BC, AD=DC. Доказать, что AC Доказательство: 1-й способ. Из равенства треугольников ABD и CBD по трем сторонам следует, что 2-й способ. Точки В и D равноудалены от концов отрезка АС, поэтому они лежат на серединном перпендикуляре к отрезку АС. Так как через две точки проходит единственная прямая, то BD — серединный перпендикуляр к отрезку АС. Отсюда AC Пример №13 (1-я замечательная точка треугольника).Доказать, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказательство: Пусть два серединных перпендикуляра к сторонам АС и АВ пересекаются в точке О (рис. 156). Точка О лежит на серединном перпендикуляре ОМ, поэтому ОА = ОС. Точка О лежит на серединном перпендикуляре ОК, поэтому ОА = ОВ. Отсюда ОВ = ОС. Поскольку точка О равноудалена от концов отрезка ВС, то она лежит на серединном перпендикуляре к отрезку ВС. Таким образом, третий серединный перпендикуляр пройдет через точку О, и все три серединных перпендикуляра к сторонам треугольника пересекутся в одной точке.
Напомню: Три признака равенства треугольников:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 💡 ВидеоГеометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать  Признаки равенства треугольников. Практическая часть. 7 класс.Скачать  Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать  Самый короткий тест на интеллект Задача Массачусетского профессораСкачать  7 класс, 15 урок, Первый признак равенства треугольниковСкачать  Высота, биссектриса, медиана. 7 класс.Скачать  Третий признак равенства треугольников | Теорема + доказательствоСкачать 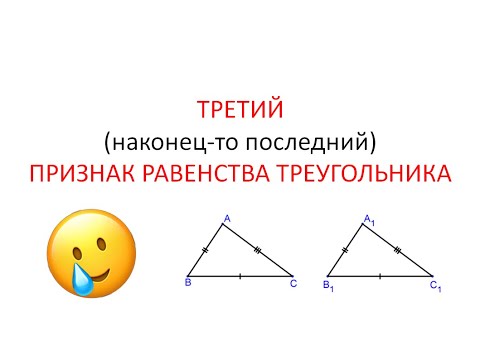 Геометрия. 7 класс. Теоремы. Т8. Третий признак равенства треугольников.Скачать 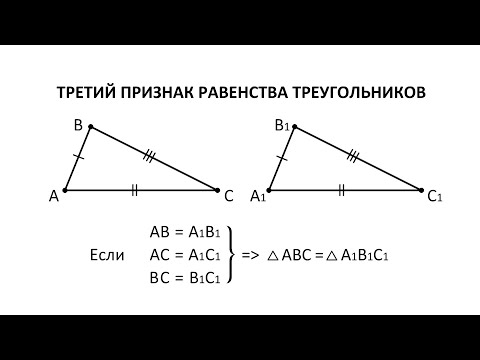 7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать  Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать  Первый признак равенства треугольников | Теорема + доказательствоСкачать  7 класс, 19 урок, Второй признак равенства треугольниковСкачать  Признаки равенства треугольников ✔️ #умскул_профильнаяматематика #никитасалливан #егэпрофильСкачать  Второй признак равенства треугольников | Теорема + доказательствоСкачать  | |||||||||||||||
 (сумма цифр числа n делится на 3)
(сумма цифр числа n делится на 3)  (число п делится на 3).
(число п делится на 3). (сумма цифр числа n делится на 3)
(сумма цифр числа n делится на 3) 
 .
. .
. .
. (ВК — медиана, проведенная к основанию)
(ВК — медиана, проведенная к основанию)  абота над структурой теоремы;
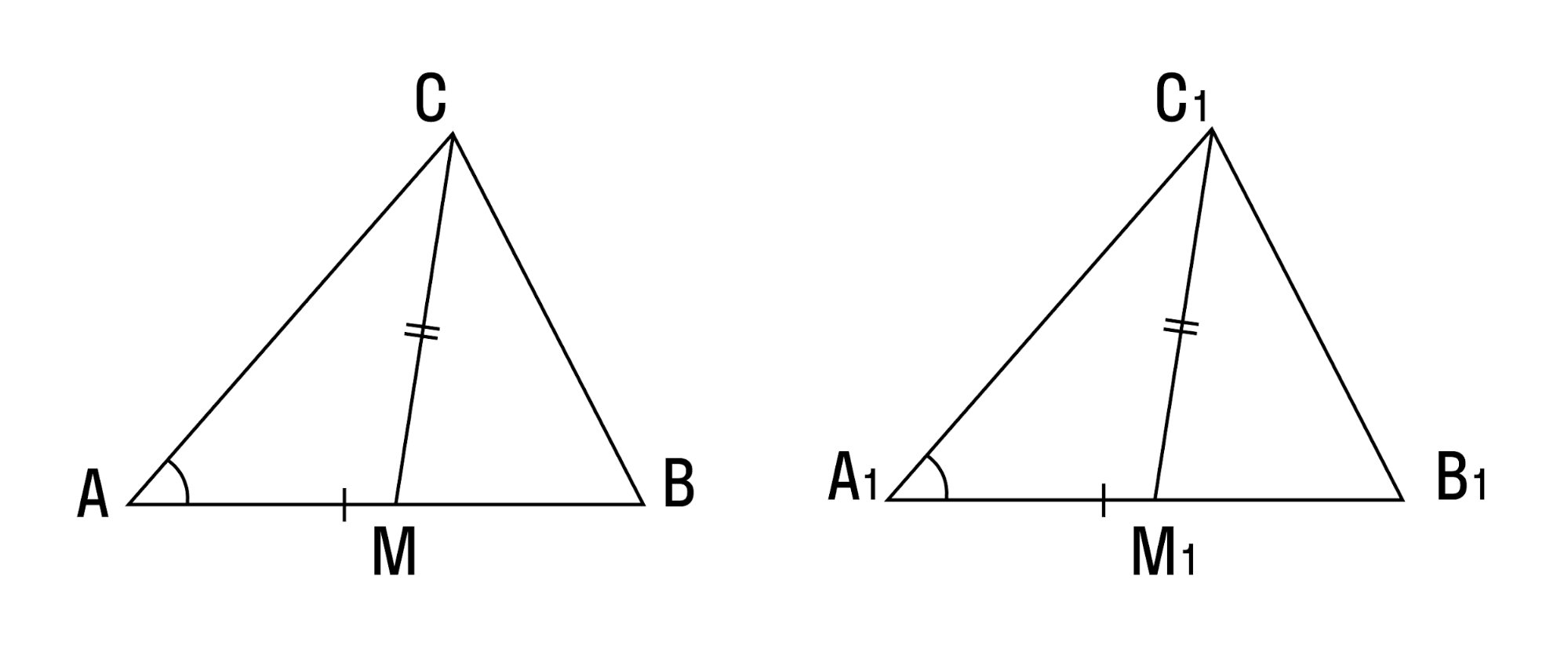
абота над структурой теоремы; артографам необходимо было нанести на карту два населенных пункта А и В (рис. 3). Измерить расстояние между пунктами оказалось невозможно, так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С, от которой можно измерить расстояние и до пункта А,и до пункта В. Измерили эти расстояния и построили на бумаге отрезки АС и СВ соответствующей длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за точку С, отложили отрезки CD и СМ,равные соответственно отрезкам СВ и СА, и соединили точки D и М отрезком.
артографам необходимо было нанести на карту два населенных пункта А и В (рис. 3). Измерить расстояние между пунктами оказалось невозможно, так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С, от которой можно измерить расстояние и до пункта А,и до пункта В. Измерили эти расстояния и построили на бумаге отрезки АС и СВ соответствующей длины (масштаб можно указать по своему усмотрению), а затем продолжили линии за точку С, отложили отрезки CD и СМ,равные соответственно отрезкам СВ и СА, и соединили точки D и М отрезком. как вертикальные углы.
как вертикальные углы. , причем
, причем  . На доске эту работу можно предложить выполнить двум-трем ученикам. После построения чертежей ставится вопрос: как проходит сторона b по отношению к сторонам угла (ас)?
. На доске эту работу можно предложить выполнить двум-трем ученикам. После построения чертежей ставится вопрос: как проходит сторона b по отношению к сторонам угла (ас)? аблица 7
аблица 7 — равнобедренный,
— равнобедренный,
 тдельно схему для случая (2) можно изобразить так (кодопозитив):
тдельно схему для случая (2) можно изобразить так (кодопозитив): хема доказательства всей теоремы может быть представлена и так:
хема доказательства всей теоремы может быть представлена и так:

 тобы провесить с помощью веревки перпендикуляр к данной прямой MN из данной на ней точки, поступают так: откладывают от этой точки О равные расстояния ОВ и ОА; прикрепляют к колышкам А и В концы веревки и, взяв веревку за середину С, натягивают ее; провешенная прямая СО и будет искомым перпендикуляром. Почему? (Рис. 6.)
тобы провесить с помощью веревки перпендикуляр к данной прямой MN из данной на ней точки, поступают так: откладывают от этой точки О равные расстояния ОВ и ОА; прикрепляют к колышкам А и В концы веревки и, взяв веревку за середину С, натягивают ее; провешенная прямая СО и будет искомым перпендикуляром. Почему? (Рис. 6.) .
. азовите теоремы, которые использовались при доказательстве данной теоремы. Какова цель их использования?
азовите теоремы, которые использовались при доказательстве данной теоремы. Какова цель их использования?




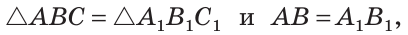 то
то 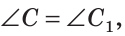 а если
а если 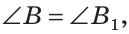 то
то 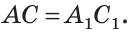
 АВС =
АВС = KNM и
KNM и  BAC =
BAC = KNM — правильные. Иногда соответствующие вершины равных треугольников обозначают одними и теми же буквами, добавляя к буквам одного из треугольников индекс:
KNM — правильные. Иногда соответствующие вершины равных треугольников обозначают одними и теми же буквами, добавляя к буквам одного из треугольников индекс:  АВС = =
АВС = =  А1В1С1. При такой записи имеют в виду, что соответствующими являются вершины А и А1, В и В1, С и С1.
А1В1С1. При такой записи имеют в виду, что соответствующими являются вершины А и А1, В и В1, С и С1.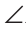 A =
A = 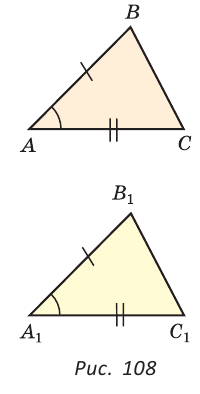
 АВС =
АВС =  А1В1С1.
А1В1С1.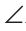 A =
A = 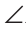 А1,
А1, 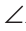 C =
C = 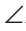 С1 (рис. 109).
С1 (рис. 109).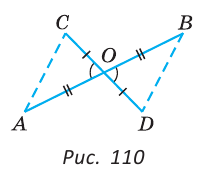
 АОС и
АОС и  BOD. У них АО = ОВ, CO = OD по условию,
BOD. У них АО = ОВ, CO = OD по условию,  AOC =
AOC = 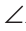 BOD как вертикальные. Треугольники равны по двум сторонам и углу между ними, то есть по 1-му признаку равенства треугольников. Стороны АС и BD равны, так как в равных треугольниках против равных углов лежат равные стороны.
BOD как вертикальные. Треугольники равны по двум сторонам и углу между ними, то есть по 1-му признаку равенства треугольников. Стороны АС и BD равны, так как в равных треугольниках против равных углов лежат равные стороны.
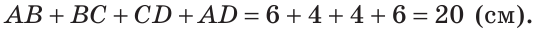
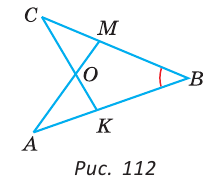
 ABD =
ABD = DCA по 2-му признаку равенства треугольников (сторона AD — общая, углы при стороне AD соответственно равны по условию), то АВ = DC,
DCA по 2-му признаку равенства треугольников (сторона AD — общая, углы при стороне AD соответственно равны по условию), то АВ = DC, 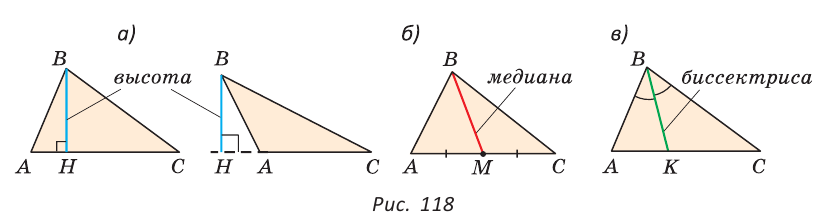
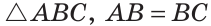 (рис. 126).
(рис. 126).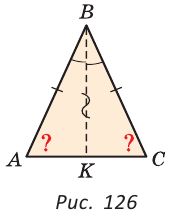
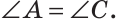
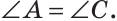 Теорема доказана.
Теорема доказана.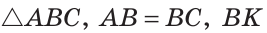 — биссектриса (рис. 127).
— биссектриса (рис. 127).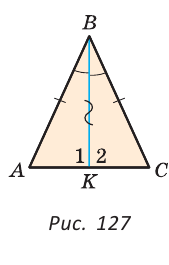
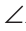 1 =
1 =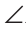 2. Так как углы 1 и 2 смежные, то их сумма равна 180°, поэтому
2. Так как углы 1 и 2 смежные, то их сумма равна 180°, поэтому 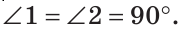 Следовательно, ВК — медиана и высота. Теорема доказана.
Следовательно, ВК — медиана и высота. Теорема доказана.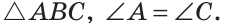
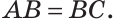
 АВС — равнобедренный. Теорема доказана.
АВС — равнобедренный. Теорема доказана.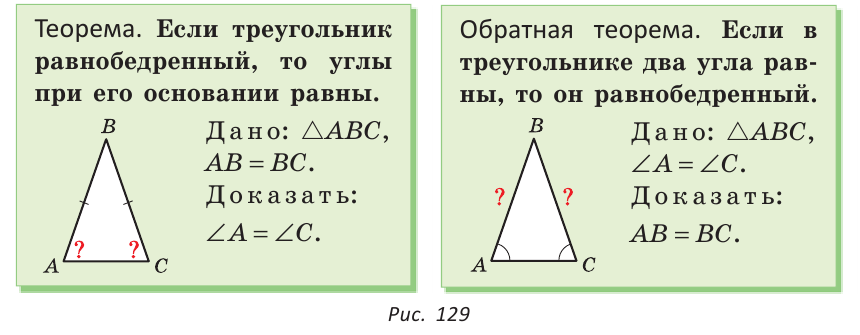
 АВС АВ =ВС, АК и СМ — биссектрисы (рис. 130). Нужно доказать, что АК = СМ. Рассмотрим
АВС АВ =ВС, АК и СМ — биссектрисы (рис. 130). Нужно доказать, что АК = СМ. Рассмотрим  АКВ и
АКВ и  СМВ. У них
СМВ. У них 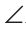 B — общий, АВ = ВС по условию,
B — общий, АВ = ВС по условию, 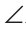 BAK =
BAK =  BCM как половины равных углов А и С при основании равнобедренного треугольника. Тогда
BCM как половины равных углов А и С при основании равнобедренного треугольника. Тогда 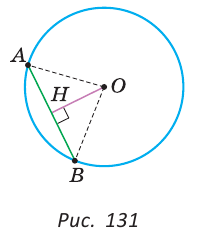
 АВС (рис. 136).
АВС (рис. 136).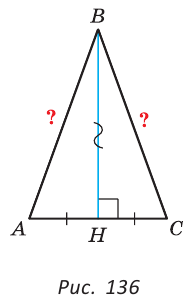
 АВН и
АВН и  СВН. У них сторона ВН — общая,
СВН. У них сторона ВН — общая, 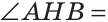
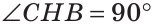 (так как ВН — высота), АН = СН (так как ВН — медиана). Треугольники АВН и СВН равны по двум сторонам и углу между ними. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.
(так как ВН — высота), АН = СН (так как ВН — медиана). Треугольники АВН и СВН равны по двум сторонам и углу между ними. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана. АВС.
АВС.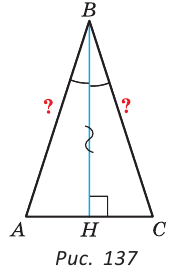
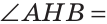
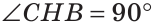 (так как ВН — высота),
(так как ВН — высота), 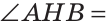
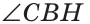 (так как ВН — биссектриса). Треугольники АВН и СВН равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.
(так как ВН — биссектриса). Треугольники АВН и СВН равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана. АВС — равнобедренный с основанием ВС и АВ =АС. Так как высота ВМ является и биссектрисой, то
АВС — равнобедренный с основанием ВС и АВ =АС. Так как высота ВМ является и биссектрисой, то  АВС — равнобедренный с основанием АС и АВ = ВС. Тогда
АВС — равнобедренный с основанием АС и АВ = ВС. Тогда  АВС — равносторонний,
АВС — равносторонний, 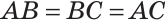
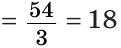 (см).
(см). АВС (рис. 139).
АВС (рис. 139).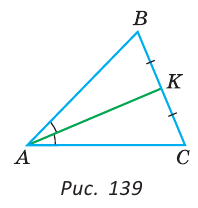
 АВС — равнобедренный по признаку равнобедренного треугольника и АВ=АС. Так как ВК = СК, то сумма отрезков АС и СК равна полупериметру
АВС — равнобедренный по признаку равнобедренного треугольника и АВ=АС. Так как ВК = СК, то сумма отрезков АС и СК равна полупериметру  АВС, то есть 18 см. По условию периметр
АВС, то есть 18 см. По условию периметр  АКС равен 30 см, поэтому АК = 30 — 18 = 12 (см).
АКС равен 30 см, поэтому АК = 30 — 18 = 12 (см).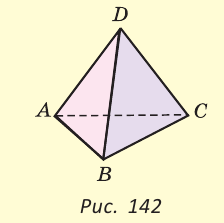
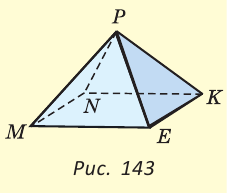
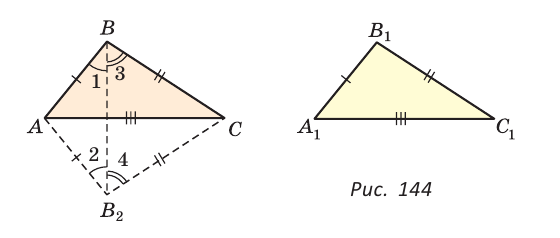
 АВС =
АВС =  А1В1С1.
А1В1С1.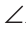 l =
l =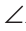 2 и
2 и 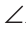 3 =
3 =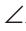 4 (как углы при основании равнобедренного треугольника). Тогда
4 (как углы при основании равнобедренного треугольника). Тогда 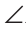 ABC =
ABC = AB2C, и треугольники ABC и АВ2С равны по двум сторонам и углу между ними. Следовательно,
AB2C, и треугольники ABC и АВ2С равны по двум сторонам и углу между ними. Следовательно, 
 B =
B =  D и луч АС — биссектриса угла BAD.
D и луч АС — биссектриса угла BAD.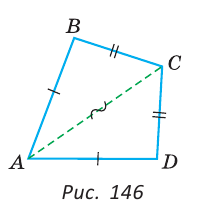
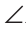 B =
B =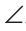 D и
D и 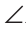 BAC =
BAC =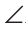 DAC как соответствующие в двух равных треугольниках и луч АС — биссектриса угла BAD.
DAC как соответствующие в двух равных треугольниках и луч АС — биссектриса угла BAD.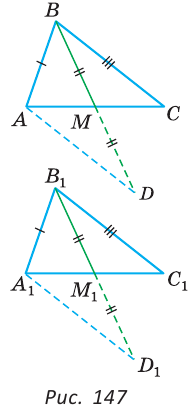
 АВС =
АВС = А1В1С1. Продлим в каждом треугольнике данную медиану на ее длину так, что MD = ВМ, M1D1=B1M1. Так как
А1В1С1. Продлим в каждом треугольнике данную медиану на ее длину так, что MD = ВМ, M1D1=B1M1. Так как  AMD =
AMD =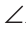 CMB как вертикальные, ВМ = MD по построению), то AD = BC. Аналогично
CMB как вертикальные, ВМ = MD по построению), то AD = BC. Аналогично 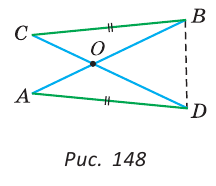
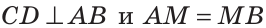 (рис. 152).
(рис. 152).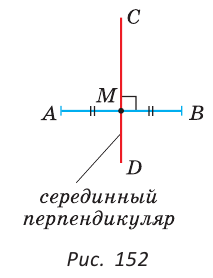
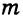 — серединный перпендикуляр к отрезку
— серединный перпендикуляр к отрезку 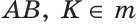 (рис. 153).
(рис. 153).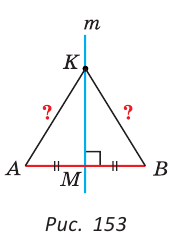
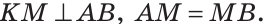 Тогда в треугольнике АКВ высота КМ является медианой. По признаку равнобедренного треугольника
Тогда в треугольнике АКВ высота КМ является медианой. По признаку равнобедренного треугольника 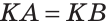 (рис. 154).
(рис. 154).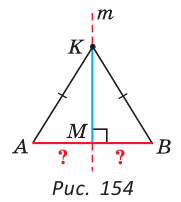
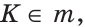 где
где 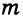 — серединный перпендикуляр к отрезку АВ.
— серединный перпендикуляр к отрезку АВ.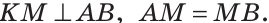 Прямая
Прямая 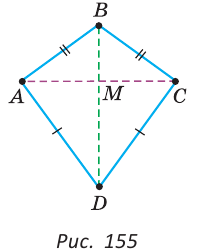
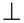 BD.
BD.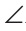 ABD =
ABD =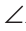 CBD. В равнобедренном треугольнике ABC биссектриса ВМ является и высотой. Поэтому AC
CBD. В равнобедренном треугольнике ABC биссектриса ВМ является и высотой. Поэтому AC