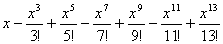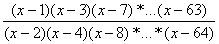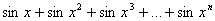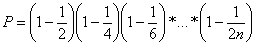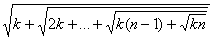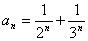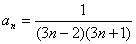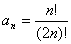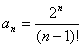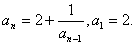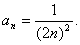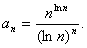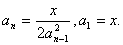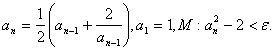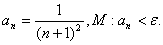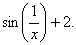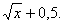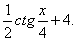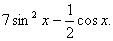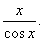Стартовая
Основы программирования
Программирование на JAVA
Программирование на C++
Программирование на Pascal
Задачи по программированию
Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

Навигация
6.4. Задачи по теме «Циклы»
6.4.1. Цикл с параметром
1. Имеется серия измерений элементов треугольника. Группы элементов пронумерованы. В серии в произвольном порядке могут встречаться такие группы элементов треугольника:
1) основание и высота;
2) две стороны и угол между ними (угол задан в радианах);
Разработать программу, которая запрашивает номер группы элементов, вводит соответствующие элементы и вычисляет площадь треугольника. Вычисления прекратить, если в качестве номера группы введен 0.
2. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?
3. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько амеб будет через 3, 6, 9, 12. 24 часа.
4. Около стены наклонно стоит палка длиной х м. Один ее конец находится на расстоянии у м от стены. Определить значение угла а между палкой и полом для значений х = k м и у, изменяющегося от 2 до 3 м с шагом h м.
5. У гусей и кроликов вместе 64 лапы. Сколько может быть кроликов и гусей (указать все сочетания)?
6. Составить алгоритм решения задачи: сколько можно купить быков, коров и телят, платя за быка 10 руб., за корову — 5 руб., а за теленка — 0,5 руб., если на 100 руб. надо купить 100 голов скота?
7. Доказать (путем перебора возможных значений), что для любых величин А, В, С типа Boolean следующие пары логических выражений имеют одинаковые значения (эквивалентны):
а) A OR В и В OR A;
б) A AND В и В AND A;
в) (A OR В) OR С и A OR С;
г) (A AND В) AND С и A AND (В AND С);
д) A AND (A OR В) и А;
е) A OR (A AND В) и А;
ж) A AND (В OR С) и (A AND В) OR (A AND С);
з) A OR (В AND С) и (A OR В) AND (A OR С).
8. Составить программу для проверки утверждения: «Результатами вычислений по формуле х2 + х + 17 при 0 ≥ х ≥ 15 являются простые числа». Все результаты вывести на экран.
9. Составить программу для проверки утверждения: «Результатами вычислений по формуле x2 + x + 41 при 0 ≥ х ≥ 40 являются простые числа». Все результаты вывести на экран.
10. Составить программу-генератор простых чисел, в основу положить формулу 2х2 + 29 при 0 ≥ х ≥ 28.
11. Составить программу-генератор простых чисел, в основу положить формулу

12. Составить программу-генератор чисел Пифагора а, b, с (с2 = а2 + b2). В основу положить формулы: a = m2 — n2, b = 2тп, с= m2+ п2 (т, п — натуральные, 1 < 
Видео:Вещдок (HD): расследование дела "Равнобедренный треугольник"Скачать

III . Программирование циклических алгоритмов.
3.1. Имеется серия измерений элементов треугольника. Группы элементов пронумерованы. В серии в произвольном порядке могут встречаться такие группы элементов треугольника:
1) основание и высота; 2) две стороны и угол между ними (угол в градусах); 3) три стороны. Разработать программу, которая запрашивает номер группы элементов, вводит соответствующие элементы и вычисляет площадь треугольника. Вычисления прекратить, если в качестве номера группы введен 0.
3.2. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой путь пробежал спортсмен за 7 дней?
3.3. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько амеб будет через 3, 6, 9, 12, …, 24 часов.
3.4. Около стены наклонно стоит палка х м. Один ее конец находится на расстоянии y м. от стены. Определить значение угла α между палкой и полом для значений x = k м. и y , изменяющегося от 2 до 3 м. с шагом h м.
3.5. У гусей и кроликов 64 лапы. Сколько могло быть кроликов и гусей (указать все сочетания которые возможны)?
3.6. Составить алгоритм решения задачи: сколько можно купить быков, коров и телят, платя за быка 10 руб., за корову – 5 руб., а за теленка – 0,5 руб., если на 100 руб. надо купить 100 голов скота?
3.7. Составить программу для проверки утверждения: «результатами вычислений по формуле x 2 + x +17 при 0≤х≤15 являются простые числа». Все результаты вывести на экран.
3.8. Составить программу для проверки утверждения: «результатами вычислений по формуле x 2 + x +41 при 0≤х≤40 являются простые числа». Все результаты вывести на экран.
3.9. Составить программу –генератор чисел Пифагора a , b , c ( c 2 = a 2 + b 2 ). В основу положить формулы : a = m 2 — n 2 , b =2 mn , c = m 2 + n 2 ( m , n – натуральные, 1 m k , 1 n k , k – данное число). Результат вывести на экран в виде таблицы из пяти столбцов: m , n, a, b, c.
3.10. Покупатель должен заплатит в кассу S руб. У него имеются 1, 2, 5, 10, 50, 100, 500 руб. Сколько купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных?
3.11. Ежемесячная стипендия студента составляет A руб., а расходы на проживание превышают стипендию и составляют B руб. в месяц. Рост цен ежемесячно увеличивает расходы на 3%. Составьте программу расчета необходимой суммы денег, которую надо единовременно попросить у родителей, чтобы можно прожить учебный год (10 месяцев), используя эти деньги и стипендию.
3.12. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в десятичной системе счисления.
3.13. Составьте программу, которая печатает таблицу умножения и сложения натуральных чисел в шестнадцатеричной системе счисления.
3.14. Найти сумму всех n -значных чисел (1≤ n ≤4).
3.15. Найти сумму всех n -значных чисел, кратных k (1≤ n ≤4).
3.16. Покажите, что для всех n =1, 2, 3, 4… n :
(1 5 +2 5 +…+ n 5 ) + (1 7 +2 7 +…+ n 7 )=2(1+2+…+ n ) 4 .
3.17. Замените буквы цифрами, так чтобы соотношение оказалось верным (одинаковым буквам соответствуют одинаковые цифры, разным – разные):
ХРУСТ * ГРОХОТ = РРРРРРРРРРР.
3.18. Составить программу, которая запрашивает пароль (например, четырехзначное число) до тех пор, пока он не будет правильно введен.
3.19. Дано натуральное число N . Вычислить:
3.20. Дано натуральное число N . Вычислить:
3.21. Дано натуральное число N . Вычислить произведение первых N множителей:
3.22. Дано натуральное число N . Вычислить:
3.23. Дано действительное число x . Вычислить:
3.24. Дано действительное число x , натуральное число N . Вычислить:
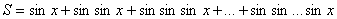
n раз
3.25. Дано действительное число a , натуральное число n . Вычислить:
3.26. Дано действительное число a , натуральное число n . Вычислить:
3.27. Дано действительное число a , натуральное число n . Вычислить:
3.28. Дано действительное число x . Вычислить:
3.29. Вычислить:
3.30. Дано действительное число x , натуральное число n . Вычислить:
3.31. Дано натуральное число n . Вычислить:
S =1*2+2*3*4+…+ n *( n +1)*…*2 n .
3.32. Дано натуральное число n . Вычислить:
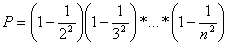
3.33. Дано натуральное число n . Вычислить:
3.34. Дано натуральное число n . Вычислить:
S =1!+2!+3!+…+ n ! , n >1).
3.35. Дано натуральное число n . Вычислить:
3.37. Дано натуральное число n . Вычислить: y =1*3*5*…*(2 n -1).
3.38. Дано натуральное число n . Вычислить: y =2*4*6*…*(2 n ).
3.39. Вычислить: y = cosx + cosx 2 + cosx 3 +…+ cosx n .
3.40. Вычислить : y=sin1+sin1.1+sin1.2+…+sin2.
3.41. Дано натуральные числа n и k . Вычислить:
3.42. Дано натуральное число n . Вычислить:
Дан числовой ряд и малая величина ε. Найти сумму ряда с точностью ε, общий член задан формулой:
3.43. 
3.45. 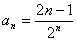
3.47. 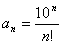
3.49. 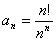
3.51. 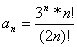
3.53. 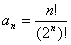
Найти наименьший номер последовательности, для которого выполняется условие | an — an -1 | ai , где i =1, 2, 3,…, n , если ε -3 .
3.55. 
3.57. 
3.59. 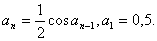
3.61. 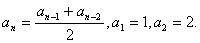
3.63. 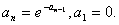
Найти наименьший номер элемента последовательности, для которого выполняется условие М. Вывести на экран этот номер и все элементы а i , где i =1, 2, 3,… n .
3.65. 
3.66. 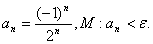
3.68.
Составить программу вычисления значений функции F ( x ) на отрезке [ a ; b ] с шагом h . Результат представить в виде таблицы, первый столбец которой – значение аргумента, второй – соответствующие значения функции:
3.75. F ( x )= x * sinx . 3.76. F(x)=
3.77. F(x)= 
3.79. F(x)= 
3.81. F ( x )= cosx + ctgx . 3.82. F(x)=
3.83. F ( x )= 
3.85. F ( x )= 
3.87. F ( x )= x 2 * sin 2 x +1. 3.88. F(x)=
3.89. F(x)=sin 2 x – cos 2x. 3.90. F(x)=
3.93. F(x)=sin x +0,5cos x. 3.94. F(x)=
3.95. Дано натуральное число n . Найти сумму первой и последней цифры этого числа.
3.96 Дано натуральное число n . Переставить местами первую и последнюю цифры этого числа.
3.97 Даны два натуральных числа m и n ( m ≤9999, n ≤9999). Проверить, есть ли в записи числа m цифры, одинаковые с цифрами в записи числа n .
3.98 Дано натуральное число n . Проверить, есть ли в записи числа три одинаковые цифры ( n ≤9999).
3.99 Дано натуральное число n ≤99. Дописать к нему цифру k в конец и в начало.
3.100 Дано натуральные числа n и k . Проверить есть ли в записи числа n k цифра m .
3.101 Среди всех n -значных чисел указать те, сумма цифр которых равна данному числу k .
3.102 Заданы три натуральных числа A , B , C , которые обозначают число, месяц и год. Найти порядковый номер даты, начиная отсчет с начала года.
3.103 Найти наименьшую и наибольшую цифры в записи данного натурального числа.
3.104 Произведение n первых нечетных чисел равно p . Сколько сомножителей взято? Если введенное n не является указанным произведением, сообщить об этом.
3.105 Найти на отрезке [ a , b ] натуральное число, имеющее наибольшее количество делителей.
3.106 Задумано некоторое число x ( x k , m , n – остатки от деления этого числа на 3, 5, 7. Найти x.
3.107 Дано натуральное число n . Проверить, будут ли все цифры числа различными.
3.108 Найти все целые корни уравнения ax 3 + bx 2 + cx + d =0, где a , b , c и d – заданные целые числа, причем a ≠0, d ≠0. Замечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d .
3.109 Дано натуральное число n . Поменять местами порядок следования цифр в этом числе на обратный или сообщить, что это невозможно в силу переполнения.
3.110 Найти все делители натурального числа n .
3.111 Натуральное число М называется совершенным, если оно равно сумме своих делителей, включая единицу, но исключая себя. Напечатать все совершенные числа, меньше заданного N .
3.112 Составьте программу, которая по номеру дня в году выводит число и месяц в общепринятой форме (например, 33 день года – 2 февраля). Замечание: считать, что год не високосный.
3.113 Долгожитель (возраст не менее 100 лет) обнаружил однажды, что если к сумме цифр его возраста прибавить число его рождения, то как раз получится его возраст. Сколько лет долгожителю?
3.114 Дано целое число n >2. Напечатать все простые числа из диапазона [2, n ].
3.115 Даны натуральные числа m и n . Найти все натуральные числа, меньшие n , квадрат суммы цифр которых равен m .
3.116 Найти натуральное число в диапазоне от 1 до n с максимальной суммой делителей.
3.117 Даны натуральные числа p и g . Получить все делители числа g , взаимно простые с p .
3.118 Для заданных натуральных n и k определить, равно ли число n сумме k -ых степеней своих цифр.
3.119 Найти все двузначные числа, сумма квадратов цифр которых равна М.
3.120 Найти все натуральные числа, не превосходящие заданного n , которые делятся на каждую из своих цифр.
3.121 Задано натуральное число n . Найти количество натуральных чисел, не превышающих n и не делящихся ни на одно из чисел 2, 3, 5.
3.122 Пусть fn – n -й член последовательности, определяемой следующим образом: fn = — fn -1 — 2 fn -2 , f 1 =1, f 2 =-1. Покажите, что 2 n+1 -7f 2 n-1 есть полный квадрат.
3.123 Последовательность Хэмминга образуют натуральные числа, не имеющие других простых делителей, кроме 2, 3 и 5. Найти:
► первые N элементов этой последовательности;
► сумму первых N элементов;
► N -й элемент по заданному номеру N ;
► первый элемент, больший данного числа М, а также номер этого элемента в последовательности;
► сумму всех элементов с номера N по номер M .
3.124 Игрок А объявляет двузначное число от 01 до 99. Игрок В меняет местами его цифры и полученное число прибавляет к сумме его цифр. Полученный результат он объявляет игроку А. Игрок А проделывает с этим числом ту же процедуру, и так они продолжают поступать поочередно, объявляя числа. От суммы чисел берется остаток от деления на 100, поэтому объявляются лишь двузначные числа. Какие числа может объявит игрок А на начальном шаге, чтобы игрок В в некоторый момент объявил число 00?
3.125 Дано натуральное число k . Напечатать k -ю цифру последовательности 12345678910111213, в которой выписаны все натуральные числа.
3.126 Дано натуральное число k . Напечатать k -ю цифру последовательности 149162536, в которой выписаны подряд квадраты всех натуральных чисел.
3.127 Составить программу перевода натурального числа из десятичной системы счисления в двоичную.
3.128 Составить программу перевода натурального числа из десятичной системы счисления в шестнадцатеричную.
3.129 Дано натуральное число N . Переставить местами его цифры так, чтобы получилось максимальное число, записанное теми же цифрами.
3.130 Дано натуральное число N . Переставить местами его цифры так, чтобы получилось минимальное число, записанное теми же цифрами.
3.131 Для записи римскими цифрами используются символы I , V , X , L , C , D , M , обозначающие соответственно числа 1, 5, 10, 50, 100, 500, 1000. Составить программу, которая запись любого данного числа n ( n ≤ 3999) арабскими цифрами переводила бы в запись римскими цифрами.
3.132 Используя все цифры от 1 до 9 по одному разу и операции сложения и вычитания, получить в сумме 100, при условии, что цифры появляются в возрастающем или убывающем порядке. Например: 123-45-67+89=100, 98-76+54+3+21=100.
3.133 Найдите целые числа (от 1 до N ), которые при возведении в квадрат дают палиндромы, например, 26 2 =676.
3.134 Найдите целые числа-палиндромы (от 1 до N ), которые при возведении в квадрат так же дают палиндромы, например, 22 2 =484.
3.135 Найдите целые числа (от 1 до N ), которые при возведении в 3, или 4, или 5 степень дают палиндромы, например, 11 3 =1331.
3.136 Дано натуральное число N . Если это не палиндром, реверсируйте его цифры и сложите исходное число с числом, полученным в результате реверсирования. Если сумма не палиндром, то повторите те же действия и выполняйте их до тех пор, пока не получится палиндром. Например, для исходного числа 78 это выглядит так: 78+87=165; 165+561=726; 726+627=1353; 1353+3531=4884.
3.137 Составьте программу, которая печатает таблицу перевода расстояний из дюймов в сантиметры (1 дюйм = 2,5 см) для значений длин от 1 до 20 дюймов.
3.138 Даны натуральные числа от 20 до 50. Напечатать те из них, которые делятся на 3, но не делятся на 5.
3.139 Даны натуральные числа от 35 до 87. Найти и напечатать те из них, которые при делении на 7 дают остаток 1, 2 или 5.
3.140 Даны натуральные числа от 1 до 50. Найти сумму тех из них, которые делятся на 5 или на 7.
3.141 Ввести с клавиатуры 10 чисел. Если среди них есть числа, большие 15, заменить их на 15. Напечатать все полученные числа.
3.142 Ввести с клавиатуры 10 чисел – положительных и отрицательных. Заменить все отрицательные числа их модулями и напечатать все полученные 10 чисел.
3.143 Напечатать те из двузначных чисел, которые делятся на 4, но не делятся на 6.
3.144 Найти произведение двузначных нечетных чисел, кратных 13.
3.145 Найти сумму чисел от 100 до 200, кратных 17.
3.146 Ввести с клавиатуры 10 чисел. Если квадрат числа меньше 100, напечатать число и его квадрат.
3.147 В бригаде, работающей на уборке сена, имеется N сенокосилок. Первая сенокосилка работала m часов, а каждая следующая на 10 минут больше, чем предыдущая. Сколько часов проработала вся бригада?
3.148 В ЭВМ вводятся координаты N точек. Определить, сколько из них попадает в круг радиусом R с центром в точке ( a , b ).
3.149 В ЭВМ вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.
3.150 Составить программу, сокращающую обыкновенные дроби.
3.151 Задано натуральное число N . Найти количество натуральных чисел, не превосходящих N и не делящихся ни на одно из чисел 2, 3, 5.
3.152 Два двузначных числа, записанных одно за другим, образуют четырехзначное число, которое делится на их произведение. Найти эти числа.
3.153 Даны два двузначных числа А и В. Из этих чисел составили два четырехзначных числа: первое число получили путем написания сначала числа A, а затем В; для получения второго сначала записали В, а потом А. Найти числа А и В, если известно, что первое четырехзначное число нацело делится на 99, а второе – на 49.
3.154 Составьте программу вычисления суммы всех двузначных чисел.
3.155 Дано натуральное n . Получить последовательность b 1 , b 2 , . , bn , где при i =1,2. n значение bi = i !
3.157 У первоклассника Пети m рублей. Мороженое стоит k рублей. Петя решил наесться досыта мороженого, для этого он покупал по одному мороженому и съедал ее до тех пор, пока ему хватало денег. Как Пете узнать, сколько денег останется у него в конце концов? Учтите, что Петя делить еще не умеет, а умеет только вычитать и складывать. Сколько мороженых он может съесть?
3.158 Бизнесмен взял ссуду m тысяч рублей в банке под 20% годовых. Через сколько лет его долг превысит s тысяч рублей, если за это время он не будет отдавать долг?
3.159 С помощью оператора while напишите программу вывода всех четных чисел в диапазоне от 2 до 100 включительно.
3.160 С помощью оператора while напишите программу определения суммы всех нечетных чисел в диапазоне от 1 до 99 включительно.
3.161 С помощью оператора while напишите программу определения идеального веса для взрослых людей по формуле: Ид. вес = рост – 100. Выход из цикла: значение роста = 250.
3.162 Имеется кусок ткани длиной М метров. От него последовательно отрезаются куски разной длины. Все данные по использованию ткани заносятся в компьютер. Компьютер должен выдать сообщение о том, что материала не хватает, если будет затребован кусок ткани, большей длины, чем имеется.
3.163 Первоначальное напряжение в цепи равно 200 вольт. Известно, что оно меняется через каждую секунду следующим образом: через одну секунду оно уменьшается на М%, а еще через секунду увеличивается на N %, затем снова уменьшается на М%, потом уменьшается на N % и т.д. Составить программу для определения, через сколько секунд напряжение в цепи превысит 220 вольт.
3.164 Напишите программу вычисления среднего геометрического модулей двух введенных с клавиатуры целых чисел. Программа должна использовать цикл while do . Условие выхода из цикла – значение числа, равное 999.
3.165 Напишите программу, которая определит первое отрицательное число последовательности: y = sin ( i /100), i = 1,2,3…
3.166 Дано действительное число А, большее 1. Найти среди чисел 1, 1+1/2, 1+1/2+1/3, . первое, большее А и его номер.
3.167 Составить программу для вычисления числа е с точностью до 0.000001 по формуле 1/1! + 1/2! + 1/3! + .
3.168 С клавиатуры вводятся числа и последовательно суммируются. Найти количество введенных чисел, когда их сумма превысила 100.
3.169 С помощью оператора repeat напишите программу, которая требует у вас пароль, например 111, и если пароль правильный, то печатает сообщение «Молодец!»
3.170 Составьте программу вычисления степени числа a с натуральным показателем n . (Записать варианты программы с разными видами циклов while , repeat , for ).
3.171 Каждая бактерия делится на две в течение одной минуты. В начальный момент времени имеется одна бактерия. Составьте программу, которая подсчитывает количество бактерий на заданное вами целое значение момента времени.
3.172 Составьте программу получения в порядке убывания всех делителей данного числа.
3.173 Разложить число на простые множители.
3.174 Составьте программу, определяющую максимальное из всех введенных вами чисел. (Пусть признаком конца ввода чисел является введенное число 0.)
3.175 Дано действительное число b >0. Последовательность a 1 , a 2 ,… образована по следующему закону: a 1 =1, a 2 =2* a 1 +1, …, ai +1 =2* a i +1 ( i =2,3,…). Требуется получить все a 1 , a2,…, меньшие или равные b .
3.176 Даны натуральное число n и действительное x . Вычислить: x 1 

3.177 Найти наибольшее и наименьшее значение функции y = 3 x 2 + x – 4, если на заданном интервале [ a , b ] x изменяется с шагом 0,1.
3.178 Пусть a1 = 1; ak = kak-1 + 1/k (k= 2,3, …) . Дано натуральное n . Получить an .
3.179 Пусть a1 = 1; ak = ak-1/k + k (k =2,3 …) . Дано натуральное n . Получить an .
3.180 На воду опущен шар радиуса r , изготовленный из вещества плотности r ( r h : V = p h 2 (3 r — h )/3, где r — радиус шара, h — высота шарового сегмента.
3.181 Найти все двузначные числа, сумма квадратов цифр которых делится на 13.
3.182 Составить программу вывода всех трехзначных чисел, сумма цифр которого равна данному натуральному числу.
3.183 Дано натуральное число n . Составить программу, подсчитывающую количество цифр числа n , сумму его цифр и определяющую его первую цифру.
3.184 В 1202 году итальянский математик Леонард Пизанский (Фибоначчи) предложил такую задачу: пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых уже через два месяца уже получается новый приплод. Сколько кроликов будет через год, если в начале года имелась одна пара? Согласно условию задачи числа, соответствующие количеству кроликов, которые появляются через каждый месяц, составляют последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34,… Составьте программу, позволяющие найти все числа Фибоначчи, меньше заданного числа N >1.
3.185 Напишите программу, которая выведет на экран 10 строк по 5 случайных чисел в диапазоне 0…36.
Видео:Треугольник судьбы (Все серии)Скачать

Имеется серия измерений треугольника
Лабораторная работа № 7. Операторы цикла
Цикл — многократное повторение последовательности действий по некоторому условию. Известны три типа циклических алгоритмических структур: цикл с предусловием, цикл с постусловием и цикл с параметром. В VBA существуют операторы, реализующие все три типа циклов.
Цикл с предусловием (цикл-пока) — наиболее универсальная циклическая структура. Он организует выполнение операторов, составляющих тело цикла, неизвестное заранее число раз. Реализуется оператором While . Формат оператора:
Здесь Do , While , Loop – зарезервированные слова;
– выражение логического типа;
Алгоритм работы оператора следующий. Вначале вычисляется значение выражения . Если имеет значение True , выполняется ; после чего вычисление значения выражения повторяется. Если имеет значение False , оператор прекращает свою работу.
Таким образом, выход из цикла осуществляется, если логическое выражение принимает значение ложь. Истинность логического выражения проверяется вначале каждого прохождения цикла, поэтому тело цикла может не выполняться ни разу.
Цикл с постусловием (цикл-до) позволяет организовать многократное выполнение операторов, если число повторений заранее неизвестно.
Цикл с постусловием может быть записан в одном из следующих видов:
Здесь Do , Until , Loop – зарезервированные слова;
– выражение логического типа;
Оператор работает по следующему алгоритму. Вначале выполняется , после чего вычисляется значение логического выражения . Если его значение есть False, операторы, образующие , повторяются. В противном случае оператор завершает свою работу.
То есть выход из цикла осуществляется, если логическое выражение принимает значение True (истина). Поскольку значение логического выражения вычисляется в конце каждого прохождения цикла, тело цикла выполнится хотя бы один раз.
Цикл с параметром (цикл со счетчиком, цикл – для) служит для организации циклов с заранее известным числом повторений.
Здесь For , To , Step , Next – зарезервированные слова VBA ;
– простая переменная порядкового типа ;
– выражение того же типа что и , определяющее начальное значение параметра;
– выражение того же типа, определяющее конечное значение параметра;
– некоторое значение типа , задающее, на сколько изменяется значение параметра при каждом проходе цикла;
Этот оператор организует повторение группы инструкций, образующих , пока изменяется от до с указанным шагом. Цикл выполняется столько раз, сколько нужно, чтобы от достиг .
При выполнении оператора вначале вычисляется значение выражения и осуществляется присваивание = . После этого циклически повторяется:
— проверка условия , если значение выражения задано и имеет положительное значение, или >= , если значение выражения задано и имеет отрицательное значение;
— изменение значения переменной на величину, указанную после слова Step ; если не указан, он полагается равным 1.
В виде блок-схем эти циклы изображаются следующим образом.
Цикл с предусловием
Цикл с постусловием
Цикл с параметром

1. Найти сумму десяти случайных чисел.
Напишем программу, воспользовавшись циклами различных видов.
Dim sum1 As Integer, sum2 As Integer, i As Integer
‘решение задачи с помощью цикла с предусловием
Do While i > 0 ‘цикла выполненяется, пока логическое условие истинно
sum1 = sum1 + Int((10 * Rnd) + 1)
MsgBox «Сумма чисел=» & sum 1
‘решение задачи с помощью цикла с постусловием
Do ‘цикла выполненяется, пока логическое условие ложно
sum2 = sum2 + Int((10 * Rnd) + 1)
Loop Until i = 0
MsgBox » Сумма чисел =» & sum2
Заметим, что особенностью интерпретатора VBA является то, что значения переменных числовых типов перед выполнением процедуры полагаются равными 0. Поэтому в программе отсутствуют команды присваивания вида: sum 1 = 0 и sum 2=0.
2. ‘Найти максимальное из n введенных с клавиатуры чисел.
Приведем два варианта решения задачи с использованием циклов разных видов.
Dim n As Byte, k As Single, i As Byte, Max As Single
n = Val(InputBox(«Введите количество чисел»))
k = Val(InputBox(» Введите число «, » Ввод чисел «))
If i = 1 Then Max = k
If k > Max Then Max = k
MsgBox «Наибольшее из чисел » & Max
Dim n As Byte, k As Single, i As Byte, Max As Single
n = Val(InputBox(«Введите количество чисел»))
k = Val(InputBox(» Введите число «, » Ввод чисел «))
If i = 1 Then Max = k
If k > Max Then Max = k
MsgBox «Наибольшее из чисел » & Max
Если из текста программ удалить строку: If i = 1 Then Max = k , то программа будет работать корректно только в случае, когда хотя бы одно вводимое число неотрицательно. Это объясняется тем, что начальное значение переменной Max считается равным 0.
3. Найти cумму n первых членов ряда 1, 1/2, 1/3, . 1/n,…
Dim n As Byte, i As Byte, sum As Single
n = Val(InputBox(«Введите количество членов ряда»))
MsgBox » Сумма » & sum
4: Найти сумму всех четных чисел в первой десятке:
Dim j As Integer, sum As Integer
For j = 2 To 10 Step 2
MsgBox » Сумма равна » & sum
5. Написать программу, осуществляющий вывод на экран введенного числа после его проверки. Ввод должен завершиться, когда вводимое значение окажется положительным числом.
Dim d As Integer
d = Val(InputBox(«Введите положительное чиcло», «Ввод числа»))
Loop Until d > 0 And (IsNumeric(d))
MsgBox «Введеное число » & d
Задачи для самостоятельного решения
Каждый студент должен решить одну задачу из блока А, две задачи из блока Б, две задачи из блока В, две задачи из блока Г.
1. Имеется серия измерений элементов треугольника. Группы элементов пронумерованы. В серии в произвольном порядке могут встречаться такие группы элементов треугольника:
— основание и высота;
— две стороны и угол между ними (угол задан в радианах);
— три стороны.
Разработать программу, которая запрашивает номер группы элементов, вводит соответствующие элементы и вычисляет площадь треугольника. Вычисления прекратить, если в качестве номера группы введен 0.
2. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?
3. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько амеб будет через 3, б, 9, 12, . 24 часа.
4. Около стены наклонно стоит палка длиной х м. Один ее конец находится на расстоянии y м от стены. Определить значение синуса угла между палкой и полом для значений y , изменяющихся от 2 до 3 м с шагом h м.
5. У гусей и кроликов вместе 64 лапы. Сколько могло быть кроликов и гусей (указать все сочетания, которые возможны)?
6. Составить алгоритм решения задачи: сколько можно купить быков, коров и телят, платя за быка 10 р., за корову — 5 р., а за теленка — 0,5 р., если на 100 р. надо купить 100 голов скота?
7. Доказать (путем перебора возможных значений), что для любых величин А, В, С типа Boolean следующие пары логических выражений имеют одинаковые значения (эквивалентны):
— A OR В и В OR A ;
— A AND В и В AND A ;
— ( A OR В) OR С и A OR С;
— ( A AND В) AND С и A AND (В AND С);
— A AND (Л OR В) и А;
— A OR ( A AND В) и А;
— A AND (В OR С) и ( A AND В) OR ( A AND С);
— A OR (В AND С) и ( A OR В) AND ( A OR С).
8. Составить программу для проверки утверждения: “Результатами вычислений по формуле х 2 + х + 17 при 0 х 15 являются простые числа”. Все результаты вывести на экран.
9. Составить программу для проверки утверждения: “Результатами вычислений по формуле х 2 + х + 41 при 0 х 40 являются простые числа”. Все результаты вывести на экран.
10. Составить программу – генератор чисел Пифагора а, b , с (с 2 = а 2 + b 2 ). В основу положить формулы: а = m 2 — n 2 , b = 2 m •n , с = m 2 + n 2 ( m , n — натуральные, 1 m k , 1 n k , k — данное число). Результат вывести на экран в виде таблицы из пяти столбцов: m, n , а, b , с.
11. Покупатель должен заплатить в кассу S р. У него имеются 1, 2, 5, 10, 50, 100, 500 р. Сколько купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных?
12. Ежемесячная стипендия студента составляет А р., а расходы на проживание превышают стипендию и составляют В р. в месяц. Рост цен ежемесячно увеличивает расходы на 3%. Составьте программу расчета необходимой суммы денег, которую надо единовременно попросить у родителей, чтобы можно было прожить учебный год (10 месяцев), используя только эти деньги и стипендию.
13. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в десятичной системе счисления.
14. Составить программу, которая печатает таблицу умножения и сложения натуральных чисел в шестнадцатеричной системе счисления.
15. Найти сумму всех n -значных чисел (1 £ n £ 4).
16. Найти сумму всех n -значных чисел, кратных k (1 £ n £ 4).
17. Покажите, что для всех n = 1, 2, 3, … N
(1 2 +2 5 + . +n 5 )+(1 7 +2 7 + . +n 7 )=2 (1 +2+ . +n) 4 .
18. Замените буквы цифрами так, чтобы соотношение оказалось верным (одинаковым буквам соответствуют одинаковые цифры, разным — разные):
ХРУСТ • ГРОХОТ = РРРРРРРРРРР.
19. Составить программу, которая запрашивает пароль (например, четырехзначное число) до тех пор, пока он не будет правильно введен.
 |
Следующие задачи решить двумя способами: с использованием цикла с параметром и одного из двух других типов цикла.
1. Дано натуральное число n. Вычислить:
2.
 |
Дано натуральное число N. Вычислить:
3. Дано натуральное число N. Вычислить произведение первых N сомножителей:
4. 
Дано натуральное число N. Вычислить:
5. 
Дано действительное число х. Вычислить:
6. 
Даны натуральное n , действительное x . Вычислить:
7. 
Даны действительное число a , натуральное число n . Вычислить:
8. 
Даны действительное число a , натуральное число n . Вычислить:
9. Даны действительное число a, натуральное число n . Вычилить:
10.
 |
Дано действительное x . Вычислить:
12.
 |
Даны натуральное n , действительное x . Вычислить:
13.
 |
Дано натуральное n . Вычислить:
14.
 |
Дано натуральное число n. Вычислить:
15.
 |
Дано натуральное число n . Вычислить:
16. 
Дано натуральное число n . Вычислить:
17. Дано натуральное число n. Вычислить:
18. 
Числа Фибоначчи ( fn ) определяются формулами
Определить f40.
19.
 |
Дано натуральное n. Вычислить:
20.
 |
Дано натуральное n . Вычислить:
21.
 |
Вычислить:
23. 
Даны натуральные числа n и k . Вычислить:
24.
 |
Дано натуральное n . Вычислить:
Составить программу вычисления значений функции F ( x ) на отрезке [а; b] с шагом h . Результат представить в виде таблицы, первый столбец которой — значения аргумента, второй — соответствующие значения функции:
2.
📸 Видео
Места, Которые Загадочнее Бермудского ТреугольникаСкачать

Самые известные тайны Бермудского треугольника: правда или вымысел?Скачать

Мультик Трансформеры Боты Спасатели - Треугольник Гриффин РокаСкачать

Эта Находка в Бермудском Треугольнике Испугала Всех УченыхСкачать

Я оплачу Все, что ты вместишь в этот ТреугольникСкачать

Бермудский треугольник | Почему? Вопросы мироздания | DiscoveryСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Бермудский треугольник: Врата в другое измерение?Скачать

БИЛЛ САЙФЕР ВЛЮБИЛСЯ В ТРЕУГОЛЬНИКИ!!! #shorts #гравити_фолзСкачать

Гравити Фолз 2 сезон. 11 серия "Кем он оказался". Лучшие моменты.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Необъяснимые встречи | Проклятие Бермудского треугольника | DiscoveryСкачать

ВСЕ ТАЙНЫ БЕРМУДСКОГО ТРЕУГОЛЬНИКА [Топ Сикрет]Скачать
![ВСЕ ТАЙНЫ БЕРМУДСКОГО ТРЕУГОЛЬНИКА [Топ Сикрет]](https://i.ytimg.com/vi/MZY4O_ud0vg/0.jpg)
100 Фактов о Бермудском Треугольнике, о Которых Вы не ЗналиСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Что стало с "Циклопом"? | Проклятие Бермудского треугольника | DiscoveryСкачать

🌊✈️КРУШЕНИЕ САМОЛЕТА В БЕРМУДСКИЙ ТРЕУГОЛЬНИК! ВЫЖИВАНИЕ НА ОСТРОВЕ В МАЙНКРАФТ ПОСЛЕ MINECRAFTСкачать