Грань авс правильный треугольник

Геометрия | 5 — 9 классы

Построить линейный угол двугранного угла с ребром АС, если в пирамиде РАВС грань АВС – правильный треугольник, О – точка пересечения медиан, прямая РО перпендикулярна плоскости АВС.

Двугранный равен линейному PHO, PH перпендикуляр опущенный на ребро АС.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Основанием пирамиды АВСД является правильный треугольник стороны которого равны а, ребро ДА перпендикулярно к плоскости АВС, а плоскость ДВС составляет с плоскостью АВС угол 30 градусов?

Основанием пирамиды АВСД является правильный треугольник стороны которого равны а, ребро ДА перпендикулярно к плоскости АВС, а плоскость ДВС составляет с плоскостью АВС угол 30 градусов.

Найдите площадь боковой поверхности пирамиды.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

ПЛИз ХЕЛП МИ = )Плоскость a пересекает грани двугранного угла по прямым AB и AC?

ПЛИз ХЕЛП МИ = )Плоскость a пересекает грани двугранного угла по прямым AB и AC.

Две пересекающиеся прямые, лежащие в плоскости a, перпендикулярны к ребру этого угла.

Докажите, что угол BAC — линейный угол этого двугранного угла.

Видео:№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

1. BH — медиана треугольника АВС?

1. BH — медиана треугольника АВС.

Прямая МА перпендикулярна к плоскости треугольника.

Найдите угол между прямыми ВН и МА.

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Основанием пирамиды ДАВС является правильный треугольник сторона которого равна а, ребро ДА перпендикулярно к плоскости АВС а плоскость ДВС составляет с плоскостью АВС угол 30 градусов?

Основанием пирамиды ДАВС является правильный треугольник сторона которого равна а, ребро ДА перпендикулярно к плоскости АВС а плоскость ДВС составляет с плоскостью АВС угол 30 градусов.

Найдите площадь боковой поверхности пирамиды.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

В треугольнике АВС сумма углов А и В равна 90 градусов?

В треугольнике АВС сумма углов А и В равна 90 градусов.

Прямая ВД перпендикулярна к плоскости АВС.

Докажите, что СД перпендикулярна АС.

Видео:10 класс, 22 урок, Двугранный уголСкачать

В треугольнике АВС сумма углов А и В равна 90градусов?

В треугольнике АВС сумма углов А и В равна 90градусов.

Прямая ВD перпендикулярнак плоскости АВС.

Доказать, что СD перпендикулярно АС.

Видео:Стереометрия, номер 34.1Скачать

1 Через вершину В треугольника АВС проведён к его плоскости перпендикуляр ВК?

1 Через вершину В треугольника АВС проведён к его плоскости перпендикуляр ВК.

Найти линейный угол между плоскостями СКВ и АКВ 2 .

ДАВС – треугольная пирамида, АЕ перпендикулярна ДС и ВЕ перпендикулярна ДС.

Найти линейный угол для двугранного ВДСА.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Основанием пирамиды давс является правильный треугольник авс, сторона которого равна а?

Основанием пирамиды давс является правильный треугольник авс, сторона которого равна а.

Ребро да перпендикулярно к плоскости авс, а плоскость двс составляет с плоскостью авс угол 30гр.

Найдите площадь главной поверхности пирамиды.

Видео:Решение. Задача 14. ЕГЭ по математике. 2. 06. 2017 . О движках .Скачать

Дан прямоугольник АВСД и точка Р вне его плоскости?

Дан прямоугольник АВСД и точка Р вне его плоскости.

Построить линейный угол двугранного угла с ребром ДС, если точка О принадлежит отрезку АВ, прямая РО перпендикулярна плоскости АВС.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

DH — медиана треугольника АВС?

DH — медиана треугольника АВС.

Прямая АМ перпендикулярна плоскости треугольника.

Найдите угол между прямыми ВН и МА.

Перед вами страница с вопросом Построить линейный угол двугранного угла с ребром АС, если в пирамиде РАВС грань АВС – правильный треугольник, О – точка пересечения медиан, прямая РО перпендикулярна плоскости АВС?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Сумма внутреннего и внешнего углов равна 180° Находим внутренний угол при вершине b (т. Е. ∠abc) : 180 — 140 = 40° Поскольку треугольник abc — равнобедренный, следовательно углы при основании равны, следовательно∠abc = ∠acb = 40°.

Tgα = ВД(высоты) / 0, 5 * АС⇒10 / 7 = ВД / 14 ВД(высота) = 10 * 14 / 7 = 20⇒Sавс = 1 / 2 * 28 * 20 = 280.

1) 6 : 2 = 3 см — середина АВ и середина СD , так как они равны. 6 см + 3 см + 3 см = 12 см Ответ : 12 см 2) Не знаю как решать , извини. 3) Возьмем АВ за х AM = MB = x 2 Тогда MN = BN = MB 2 = x 4 AM : MN = x 2 : x 4 = 2 : 1 BN : AM = x ..

SΔ = (a * ha) / 2 SΔ = (14 * 6) / 2 = 42 см².

По твоему чертежу, но без окружности : А 0 — центр окружности I А0 — радиус I 0В — радиус I 0С — радиус I0___________C ∠А0С = ∠В0С = 90° I Соедини· А и· С I Получим равнобедренныйΔ А0С I А0 = 0С (это радиусы) I В равнобедренномΔ углы при основании B ..

1)х + х + 160 = 180 2х = 20 х = 10 2)160 + 10 = 170.

Так как треугольник авс равнобедренный ав = вс то и ам = ск тогда треугольник вмк равнобедренный.

Дано : угол АВ, угол АD = 80градусов, угол ВD, угол AC = углуCB (это равенствопоказывает то, что С — биссектриса АВ), уголAD = углуDC. Найти : уголBD Решение : 1) уголAD× 2 = углуAC уголAC = углуCB 80× 2 = 160 — угол CB 2) уголDC + уголCB = углуBD 8..

АС = 50 + 16 = 66 М = АВ / 2 = 50 / 2 = 25 см К = ВС / 2 = 16 / 2 = 8 МК = 66 — 33 = 33 см.

1) а не параллельно b, т. К. угол4 = 180 — 60 = 120градусов (т. К. угол3 и угол4 смежные)угол4 и угол 1 являются накрест лежащими, но они не равны, значит а не параллельна b. 2) угол3 + угол4 = 180градусов, т. К. они односторонние. Пусть угол3 =..

Видео:№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Система тренажеров по теме «Двугранные углы»

Разделы: Математика

Одной из основных тем в стереометрии является тема “Двугранные углы”. Несмотря на то, что понятия двугранного угла и его линейного угла учащиеся усваивают легко, возникает много затруднений при решении стереометрических задач. Анализ этих затруднений показал, что это связано с недостаточной сформированностью навыка изображения линейных углов. Чтобы преодолеть эти проблемы, необходима определенная система задач.

Предлагаемые задачи разбиты на четыре группы (тренажеры).

Тренажер №1. включает в себя задачи на доказательство того, что отмеченный на рисунке угол является линейным.

Тренажер №2. Это задачи на выделение линейного угла среди нескольких обозначенных на рисунке углов.

Тренажер №3. Это задачи на построение линейного угла данного двугранного угла.

Тренажер №4. Это задачи вычислительного характера.

Обычно такие задачи решаются по готовым рисункам на листах формата А4. На этих же листах записаны и тексты задач к данным рисункам. Листы с задачами вложены в мультифоры, что позволяет их многократно использовать как для индивидуального опроса учащихся, так и на подготовительном этапе при решении более сложных задач.

В процессе решения этих задач у учащихся не только формируются навыки построения линейных углов данных двугранных углов, но и идет повторение различных понятий, приемов решения прямоугольных треугольников, вычисления площадей, правила изображения фигур на рисунке.

1. SABCD — пирамида, прямая SB перпендикулярна плоскости АВС, ВР DС (лист 1). Доказать, что угол SРВ — линейный угол двугранного угла с ребром СD.

2. SABC — пирамида, АСВ=90 0 , прямая SB перпендикулярна плоскости АВС (лист 2). Доказать, что угол SСВ — линейный угол двугранного угла с ребром АС.

3. SABC — пирамида, АВ=ВС, D — середина отрезка АС, прямая SB перпендикулярна плоскости АВС (лист 3). Доказать, что угол SDВ — линейный угол двугранного угла с ребром AС.

1. SABC — пирамида, основание которой — правильный треугольник. Какой из отмеченных углов является линейным углом двугранного угла с ребром AС, если:

а) Е — середина отрезка АС (лист 4), прямая SB перпендикулярна плоскости АВС;
б) К — середина отрезка АС (лист 5), ON//BK и прямая SО перпендикулярна плоскости АВС?

2. SABC — пирамида, D — середина отрезка АС, прямая SB перпендикулярна плоскости АВС (лист 6). Каким должен быть треугольник АВС, чтобы линейным углом двугранного угла с ребром АС являлся угол SDB, угол SAB, угол SKB?

1. Построить линейный угол двугранного угла с ребром АС, если в пирамиде SABC:

а) АВ=ВС, прямая SB перпендикулярна плоскости АВС (лист 7);
б) грань АВС — правильный треугольник, О — точка пересечения медиан, прямая SO перпендикулярна плоскости АВС (лист 8);
в) грань АВС — правильный треугольник, О — середина отрезка АВ, прямая SO перпендикулярна плоскости АВС (лист9).

2. Дан прямоугольник АВСD и точка S не лежит в его плоскости. Построить линейный угол двугранного угла с ребром DС, если:

а) прямая SB перпендикулярна плоскости АВС (лист 10);
б) точка О принадлежит отрезку АВ, прямая SО перпендикулярна плоскости АВС (лист 11);
в) О — точка пересечения диагоналей, прямая SО перпендикулярна плоскости АВС (лист 12).

3. Дан ромб АВСD, прямая SС перпендикулярна плоскости АВС. Построить линейный угол двугранного угла с ребром ВD (лист 13).

4. Построить линейный угол двугранного угла с ребром АD, если:

а) АВСD — трапеция, ВАD=90 0 , прямая SB перпендикулярна плоскости АВС (лист 14);
б) АВСD — трапеция, ВАD=90 0 , точка О принадлежит отрезку ВС, прямая SО перпендикулярна плоскости АВС (лист 15);
в) АВСD — равнобедренная трапеция, прямая ВS перпендикулярна плоскости АВС (лист 16);
г) АВСD — равнобедренная трапеция, прямая SС перпендикулярна плоскости АВС (лист 17).

1. Дана пирамида SАВС. Найти величину двугранного угла с ребром АС, если:

а) прямая ВS перпендикулярна плоскости АВС, С=90 0 , ВС=BS=6см (лист 18);
б) прямая ВS перпендикулярна плоскости АВС, АВ=ВС=10см, ВS=АС=12см. (лист 7);
в) грань АВС — правильный треугольник, АВ=6см, О — точка пересечения медиан, прямая ОS перпендикулярна плоскости АВС, ОS=4см (лист 8);
г) грань АВС — правильный треугольник, О — середина отрезка АВ, АВ=6см, прямая ОS перпендикулярна плоскости АВС, ОS=4см (лист 9).

2. АВСD — прямоугольник, ВD=4см. Прямая SВ перпендикулярна плоскости АВС, SВ=6см, двугранный угол с ребром DС равен 60 0 . Найти стороны прямоугольника (лист 10).

3. АВСD — прямоугольник, его площадь 48 см 2 , DС=4см, прямая ОS перпендикулярна плоскости АВС, ОS=6см. Найти величину двугранного угла с ребром DС (лист 12).

4. АВСD — ромб, ВD=8см, прямая SС перпендикулярна плоскости АВС, SС=16см, двугранный угол с ребром ВD равен 45 0 Найти площадь ромба (лист 13).

5. В параллелограмме АВСD АDC=150 0 , АD=16см, DС=12см, прямая SС перпендикулярна плоскости АВС, SС=18см (лист 19). Найти величину двугранного угла с ребром АD и площадь параллелограмма.

Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Грань авс правильный треугольник

В основании треугольной пирамиды ABCD лежит правильный треугольник АВС. Боковая грань пирамиды BCD перпендикулярна основанию, BD = DC.

а) Постройте сечение пирамиды плоскостью, проходящей через ребро ВС перпендикулярно ребру AD.

б) Найдите объём пирамиды BCМD, где М — точка пересечения ребра АD и плоскости

сечения, если сторона основания пирамиды ABCD равна а боковое ребро AD наклонено к плоскости основания под углом

а) Опустим перпендикуляры из точек B и C на Они упадут в одну точку — точку M пересечения искомой плоскости с прямой BCM — искомое сечение.

б) Пусть H — середина Тогда по условию При этом Значит,

🎦 Видео

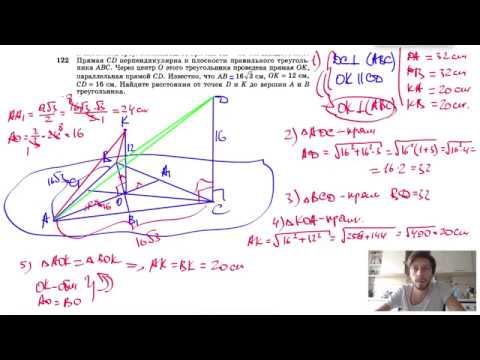
№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

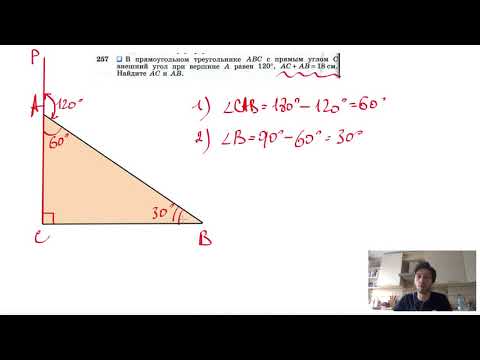
№257. В прямоугольном треугольнике ABC с прямым углом С внешний угол при вершине А равен 120°Скачать

№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

Задача 14 (С2) из проф ЕГЭ 2017 по математикеСкачать

ЕГЭ 1 задание ✧ В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найти меньший угол ∆ABCСкачать

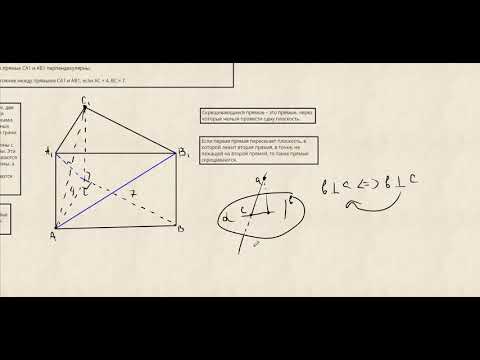
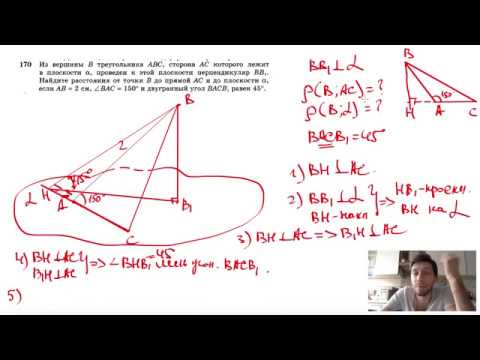
№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

В треугольнике ABC угол C равен 90°, AC = 4,8, синус A = 7/25. Найдите AB.Скачать

Задание 14 Сечение пирамиды ОбъемСкачать