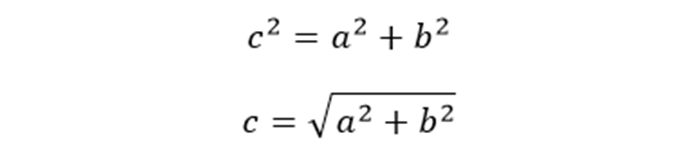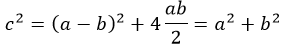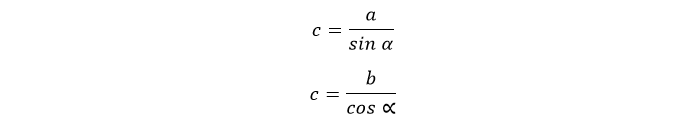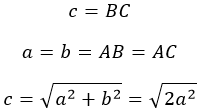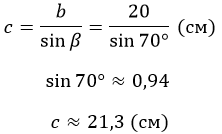Гипотенуза треугольника abc является

Что такое гипотенуза треугольника? У какого треугольника есть гипотенуза?

Гипотенуза — это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Таким образом, гипотенуза есть только в прямоугольном треугольнике.

Даже если в условии задачи прямо не сказано, что треугольник — прямоугольный, но одна из его сторон названа гипотенузой, это означает, что данный треугольник имеет и прямой угол.

Если прямой угол назван одной буквой, то в названии гипотенузы этой буквы нет.

Например, в треугольнике ABC

лежит напротив прямого угла C.

(В названии гипотенузы — AB — буквы C нет).

Как правило, в условии задачи не сказано, какая сторона треугольника является гипотенузой.

Гипотенуза определяется по положению прямого угла.

Например, в треугольнике MKF

Значит, MF — гипотенуза

(поскольку она лежит напротив прямого угла K).

Гипотенуза — самая длинная из сторон прямоугольного треугольника.

Длина гипотенузы больше длины любого катета.

Согласно неравенству треугольника, длина гипотенузы меньше суммы длин катетов.

Как найти длину гипотенузы, зная катеты и один из острых углов, мы рассмотрим позже.

Видео:H является основанием высоты из вершины прямого угла B треугольника ABC Найти AB если AH=5 AC=20Скачать

Гипотенуза треугольника

Гипотенуза треугольника — это такая сторона треугольника, длина которой равна
квадратному корню из суммы квадратов длин двух других сторон.

Можно сказать, что в треугольнике есть гипотенуза, если длину
какой-нибудь стороны можно выразить по формуле:

Это формула из Теоремы Пифагора. Где с — гипотенуза треугольника, a и b — катеты треугольника.

Не во всех треугольниках есть гипотенуза!

Признаки наличия гипотенузы в треугольнике

Существует ряд случаев / признаков по которым
можно определить, что в треугольнике есть гипотенуза:

• Прямоугольный треугольник;
• Треугольник, у которого один из углов прямой, по условию;
• Два угла треугольника по 45 градусов;
• Треугольник, к которому можно применить Теорему Пифагора;
• Если в треугольнике известны только два угла, и третий угол
  является прямым (по теореме о сумме углов треугольника);
• Квадратный корень из суммы квадратов длин двух
  сторон треугольника равен длине третьей стороне;
• По условию задачи две стороны являются катетами.
• Египетский треугольник;

Если хотя бы один из вышеперечисленных признаков верен,
соответствует условию задачи, то в треугольнике есть гипотенуза.

Пример гипотенузы в треугольнике

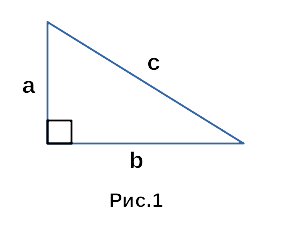
На рисунке 1 изображен прямоугольный треугольник со сторонами a, b, c.

В данном случае, определить какая сторона является гипотенузой
довольно таки просто. Стороны a и b образуют прямой угол,
поэтому сторона c — гипотенуза. Сторона c является гипотенузой
треугольника, так как два смежных с ней угла, образуют в
сумме угол в 90 градусов, т.е прямой.

Длина гипотенузы треугольника

Мы могли бы определить является ли сторона гипотенузой произвольного
треугольника, зная только величину длин всех сторон треугольника.

Как узнать есть ли гипотенуза? Какова её длина?

Допустим, длина стороны a = 3, b = 4, c = 5, тогда по Теореме Пифагора (по признаку гипотенузы в треугольнике):

Все сходится, следовательно гипотенуза в треугольнике есть, и её длина равна 5.
Если в вашем случае ответ не сходится, числа получились в
итоге разные, значит, однозначно гипотенузы в треугольнике нет!

Длину гипотенузы треугольника, можно узнать с помощью Теоремы Пифагора, только в трех базовых случаях:

1. В треугольнике известны длины двух сторон, есть прямой угол;
2. Два угла треугольника по 45 градусов, известна только одна сторона;
3. Известны длины всех сторон треугольника;

Видео:№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

Гипотенуза — формула, правила и примеры вычислений

Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».

А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).

Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.

Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.

Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.

Видео:№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать

Теорема Пифагора

Сумма квадратов катетов составляет квадрат гипотенузы:

Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.

Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.

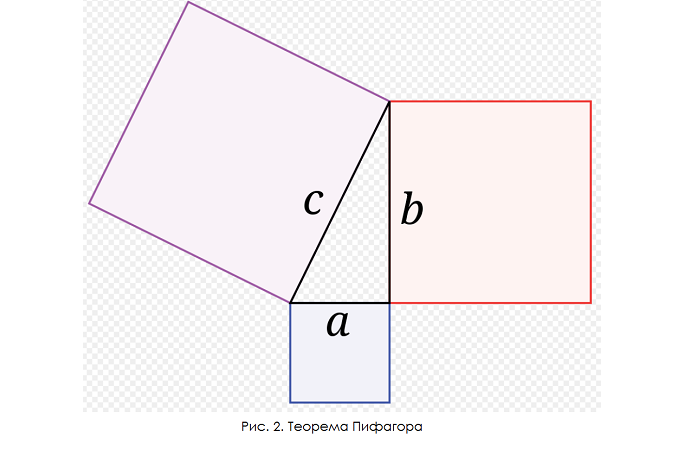
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).

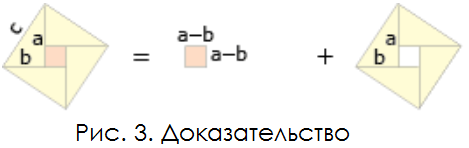
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

В тригонометрии

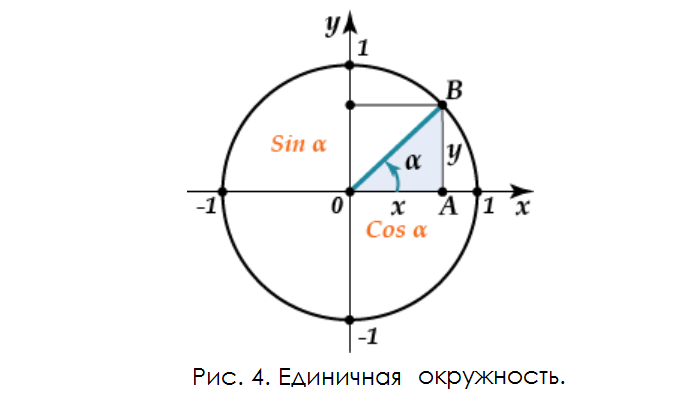
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).

На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.

В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:

sin 2 α + cos 2 α = 1

Видео:Точка H является основанием высоты, проведённой из вершины прямого угла BСкачать

Гипотенуза прямоугольного треугольника

Связана со сторонами следующими соотношениями (см. рис. 1):

a – противолежащий α катет;

Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.

Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.

Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

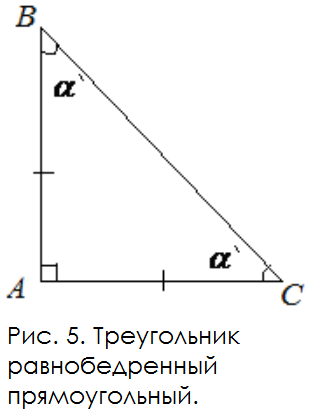
Гипотенуза равнобедренного треугольника

В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.

Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.

Видео:№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать

Пример решения задачи

Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.

AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:

Ответ: АВ = 21,3 см.

В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.

Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.

📺 Видео

Найдите гипотенузуСкачать

Точка H является основанием высотыСкачать

Геометрия На продолжении гипотенузы AB прямоугольного равнобедренного треугольника ABC за точку BСкачать

Геометрия Вне прямоугольного треугольника ABC на его гипотенузе AB построен квадрат ABFD. ДокажитеСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

№155. Через вершину прямого угла С равнобедренного прямоугольного треугольника ABCСкачать

На гипотенузе AB прямоугольного треугольника ABC выбрана такая точка D, что BD = BC, а на катетеСкачать

Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Пятнадцатое задание ОГЭ по математике (4) #огэ #огэ2023 #огэпоматематике #математика #огэматематикаСкачать

Геометрия На гипотенузе AB прямоугольного треугольника ABC отмечена точка M так что AM:BM = 1:3Скачать

№484. В прямоугольном треугольнике а и b — катеты, с — гипотенуза. Найдите b, если:Скачать

Медиана в прямоугольном треугольникеСкачать

ОГЭ как найти тангенс угла, если нет треугольника #математика #огэ #огэматематика #геометрияСкачать