Фрактал треугольник серпинского c (5 видео)

C# Разработка

Блог о создании приложений на платформе .NET Framework

Содержание

7 октября 2018 г.
Треугольник Серпинского методом хаоса. Программа на C# с исходным кодом.
Предыстория
Треугольник Серпинского методом хаоса.
Правила и примеры.
4 комментария:
Треугольник Серпинского
Некоторые свойства
Варианты
Треугольник Серпинского и треугольник Паскаля
Что это?
И что с того?
🌟 Видео

Видео:Математика вприпрыжку: рисуем треугольный фрактал. Треугольник СерпинскогоСкачать

7 октября 2018 г.

Треугольник Серпинского методом хаоса. Программа на C# с исходным кодом.

Видео:Что Такое Фракталы? Простое Объяснение!Скачать

Предыстория

Просматривая youtube, я наткнулся на интересное видео, в котором был показан пример создания фракталов используя очень простые правила:

Мы имеем несколько опорных точек на плоскости. Все они пронумерованы.
Устанавливаем начальную произвольную точку с которой начнётся построение. Будем её называть текущей точкой.
Возьмём генератор случайных чисел в дапозоне от 1 до количества опорных точек. В зависимости от сгенерированного числа выбираем опорную точку под этим номером, после чего строим новую точку по середине (1/2 расстояния) от текущей до опорной точки. Это будет новая текущая точка для следущей итерации, после чего операцию повторяем действия до бесконечности.

Ссылка на то видео:

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Треугольник Серпинского методом хаоса.

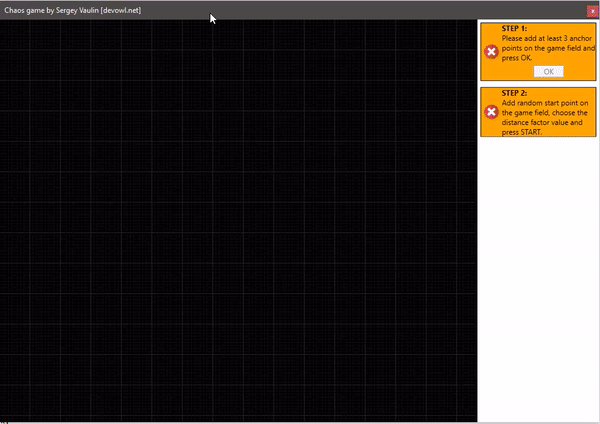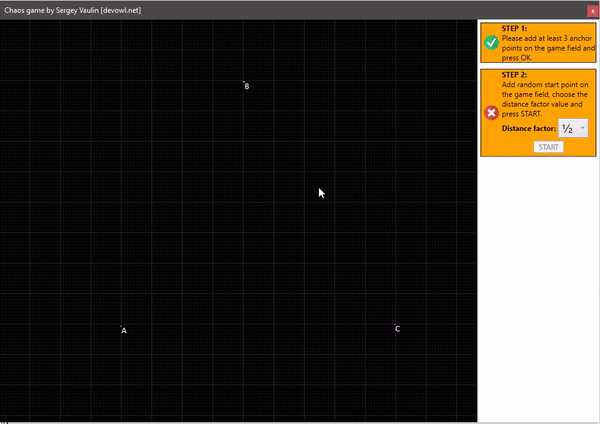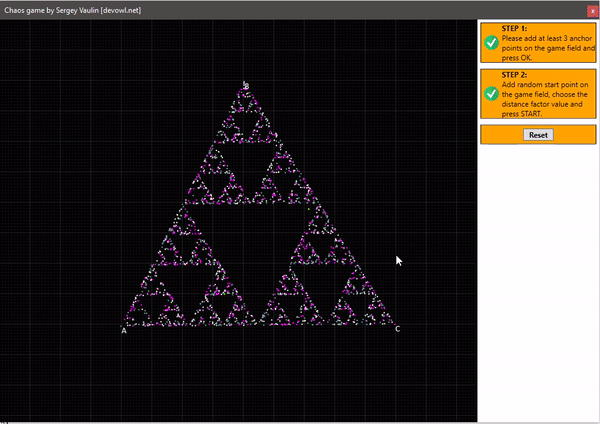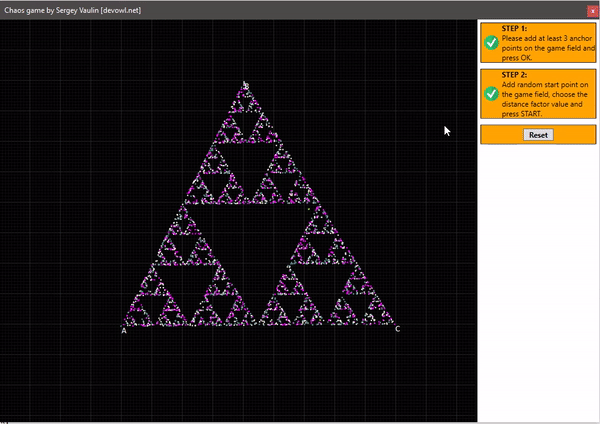
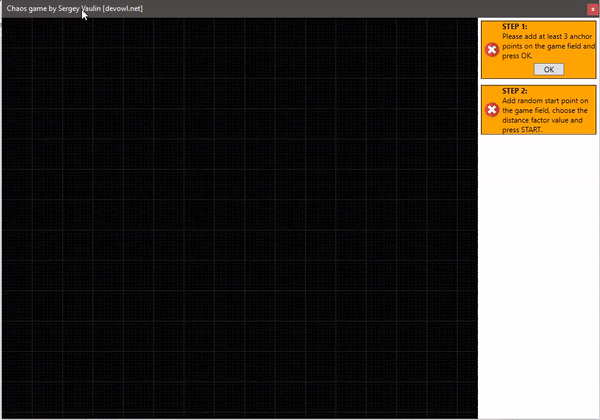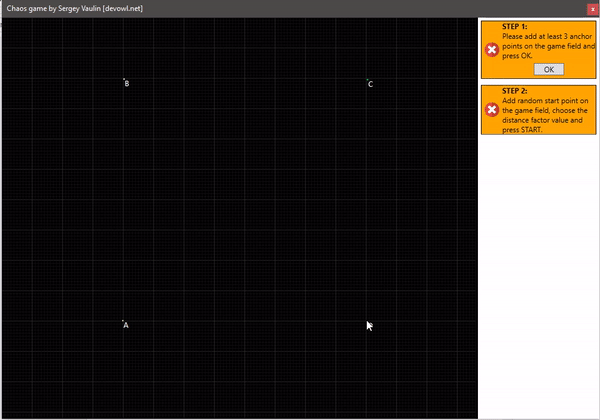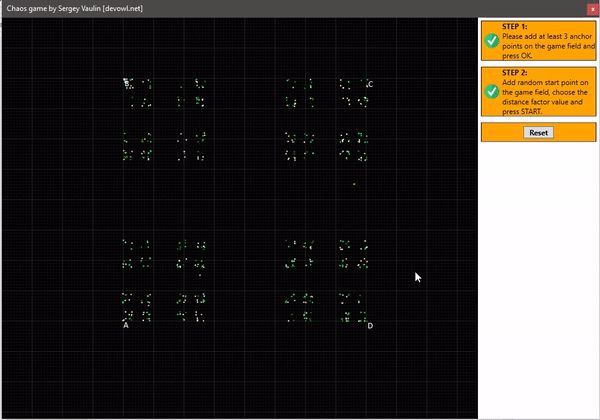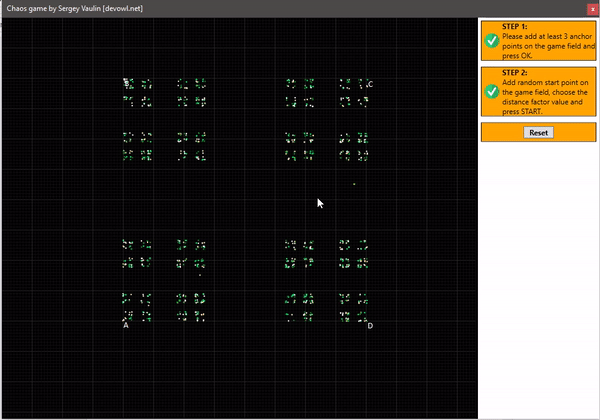
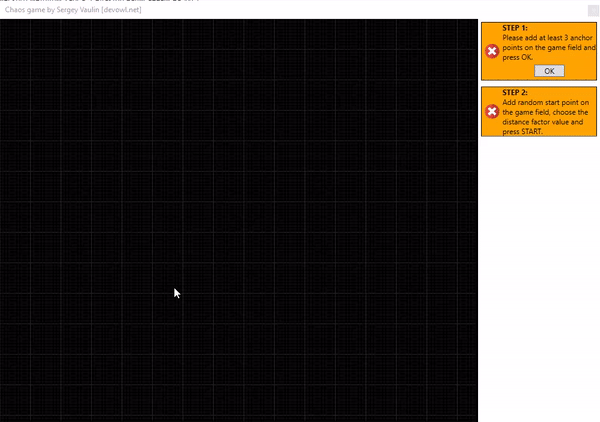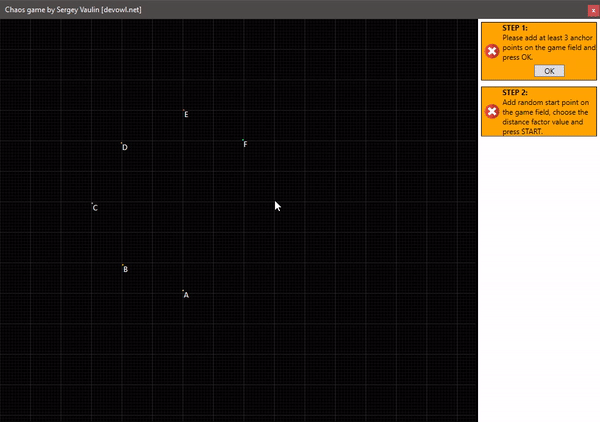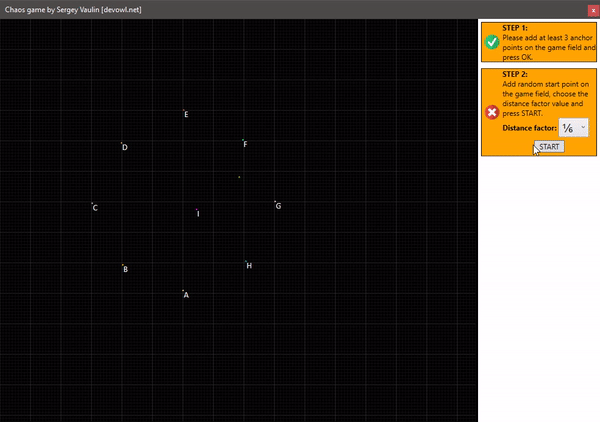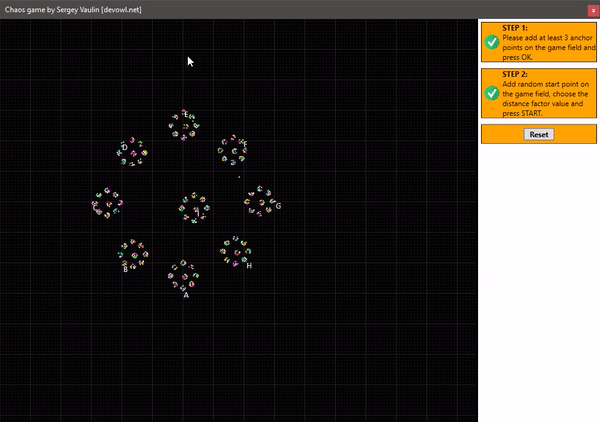
Если следовать этим правилам, то на трёх точках мы получим достаточно интересный результат. Для этого мной было написано приложение, которое даёт возможность потестировать это, и увидеть воочию построение. Вот записанное видео с результатом:

Как видите, мы получили фигуру из само подобных треугольников, её научное название «треугольник Серпинского«. При этом удивительно, что у нас остаются не закрашенные области сколько бы раз мы не запускали приложение. Схематическое изображение треугольника представлено ниже:

И я считаю это удивительно получить столь изящную фигуру выбрасыванием случайного числа.

Видео:Аудиокнига АллатРа с.504 - 512. Фракталы: треугольники Серпинского, снежинка КохаСкачать

Правила и примеры.

Теперь представьте, что мы берём не середину расстояния (1/2) а к примеру треть (1/3), тогда можно увидеть не менее интересные картинки.

Построение для 3 точек:

Построение для 4 точек:

Построение круга с 1 центральной точкой и отступом 1/6:

На этом все, исходный код и само приложение можно найти по ссылке в начале статьи.

Спасибо за внимание!

4 комментария:

Поточечное прорисовывание электронами интерференционной картины за двумя щелями в эксперименте В. А. Фабриканта «отдыхает». В Википедии по поводу треугольника Серпинского есть ссылка на мою статью в журнале «В мире науки» (1989, №9.) Я с помощью элементарной цветографической символики в полной мере и геометрически наглядно вскрыл фрактальную организацию простых делителей в арифметическом треугольнике Паскаля. Так вот, точки единичных актов в построении т-ка Серпинского методом хаоса ложатся на «бесцветные перемычки» в цветографическом представлении распределения простого делителя 2 по степеням. То есть, на числа треугольника Паскаля, где он отсутствует. А в целом, построение т-ка Серпинского методом хаоса на элементарном (и потому особо ценном) уровне показывает, что такое нынешняя органичная фрактальная геометризация теории вероятностей. Ведь вероятность попадания очередного акта (очередной точки) на плоскости непосредственно выражается через фрактальную размерность т-ка Серпинского.

Я сам не программист, но есть одно предположение. Хотелось бы проверить. Можете сделать так, что бы последовательность случайных чисел (от 1 до 42) подгружалась из отдельного файла (например *.txt). А вершины треугольника можно было бы нумеровать несколькими цифрами: Вершина А (1,2. 14), вершина В (15,16. 28), вершина С (29,30. 42).

К сожалению пока такого рода доработку делать не буду

Видео:Треугольник Серпинского ФракталыСкачать

Треугольник Серпинского

Для просмотра анимации необходимо включить JavaScript.

Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.

Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.

Следующий способ получить треугольник Серпинского еще больше похож на обычную схему построения геометрических фракталов с помощью замены частей очередной итерации на масштабированный фрагмент. Здесь на каждом шаге составляющие ломаную отрезки заменяются на ломаную из трех звеньев (она сама получается в первой итерации). Откладывать эту ломаную нужно попеременно то вправо, то влево. Видно, что уже восьмая итерация очень близка к фракталу, и чем дальше, тем ближе будет подбираться к нему линия.

Но и на этом не всё. Оказывается, треугольник Серпинского получается в результате одной из разновидностей случайного блуждания точки на плоскости. Этот способ называется «игрой Хаос». С его помощью можно построить и некоторые другие фракталы.

Суть «игры» такова. На плоскости зафиксирован правильный треугольник A₁A₂A₃. Отмечают любую начальную точку B₀. Затем случайным образом выбирают одну из трех вершин треугольника и отмечают точку B₁ — середину отрезка с концами в этой вершине и в B₀ (на рисунке справа случайно выбралась вершина A₁). То же самое повторяют с точкой B₁, чтобы получить B₂. Потом получают точки B₃, B₄, и т. д. Важно, чтобы точка «прыгала» случайным образом, то есть чтобы каждый раз вершина треугольника выбиралась случайно, независимо от того, что было выбрано в предыдущие шаги. Удивительно, что если отмечать точки из последовательности B_i, то вскоре начнет проступать треугольник Серпинского. Ниже изображено, что получается, когда отмечено 100, 500 и 2500 точек.

Некоторые свойства

Фрактальная размерность log₂3 ≈ 1,584962. . Треугольник Серпинского состоит из трех копий самого себя, каждая в два раза меньше. Взаимное расположение их таково, что если уменьшить клеточки сетки в два раза, то число квадратиков, пересекающихся с фракталом, утроится. То есть N(δ/2) = 3N(δ). Если сначала размер клеток был 1, а с фракталом пересекалось N₀ из них (N(1) = N₀), то N(1/2) = 3N₀, N(1/4) = 3 2 N₀, . N(1/2 k ) = 3 k N₀. Отсюда получается, что N(δ) пропорционально , и по определению фрактальной размерности она равна как раз log₂3.
Треугольник Серпинского имеет нулевую площадь. Это означает, что в фрактал не влезет ни один, даже очень маленький, кружок. То есть, если отталкиваться от построения первым способом, из треугольника «вынули» всю внутренность: после каждой итерации площадь того, что остается, умножается на 3/4, то есть становится всё меньше и стремится к 0. Это не строгое доказательство, но другие способы построения могут только усилить уверенность, что это свойство всё-таки верно.
Неожиданная связь с комбинаторикой. Если в треугольнике Паскаля с 2 n строками покрасить все четные числа белым, а нечетные — черным, то видимые числа образуют треугольник Серпинского (в некотором приближении).

Варианты

Ковер (квадрат, салфетка) Серпинского. Квадратная версия была описана Вацлавом Серпинским в 1916 году. Ему удалось доказать, что любая кривая, которую можно нарисовать на плоскости без самопересечений, гомеоморфна какому-то подмножеству этого дырявого квадрата. Как и треугольник, квадрат можно получить из разных конструкций. Справа изображен классический способ: разделение квадрата на 9 частей и выбрасывание центральной части. Затем то же повторяется для оставшихся 8 квадратов, и т. д.

Как и у треугольника, у квадрата нулевая площадь. Фрактальная размерность ковра Серпинского равна log₃8, вычисляется аналогично размерности треугольника.

Пирамида Серпинского. Один из трехмерных аналогов треугольника Серпинского. Строится аналогично с учетом трехмерности происходящего: 5 копий начальной пирамиды, сжатой в два раза, составляют первую итерацию, ее 5 копий составят вторую итерацию, и т. д. Фрактальная размерность равна log₂5. У фигуры нулевой объем (на каждом шаге половина объема выбрасывается), но при этом площадь поверхности сохраняется от итерации к итерации, и у фрактала она такая же, как и у начальной пирамиды.

Губка Менгера. Обобщение ковра Серпинского в трехмерное пространство. Чтобы построить губку, нужно бесконечное повторение процедуры: каждый из кубиков, из которых состоит итерация, делится на 27 втрое меньших кубиков, из которых выбрасывают центральный и его 6 соседей. То есть каждый кубик порождает 20 новых, в три раза меньших. Поэтому фрактальная размерность равна log₃20. Этот фрактал является универсальной кривой: любая кривая в трехмерном пространстве гомеоморфна некоторому подмножеству губки. У губки нулевой объем (так как на каждом шаге он умножается на 20/27), но при этом бесконечно большая площадь.

Видео:Как нарисовать фрактал треугольник Серпинского.Скачать

Треугольник Серпинского и треугольник Паскаля

Что это?

Треугольник Серпинского

Треугольник Серпинского — один из известнейших фракталов, его построение — одна из первых лабораторных работ на рекурсию по соответствующим дисциплинам во многих ВУЗах. Выглядит фрактал следующим образом:

Треугольник Паскаля

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.

И что с того?

Есть в треугольнике Паскаля интересная особенность. Он отображает вышеупомянутый фрактал своими числами. Если долго всматриваться в ~~бездну, бездна начинает всматриваться в тебя~~ значения, то можно увидеть, что чётные и нечетные числа располагаются группами, ибо есть одно негласное всем известное правило: четное+нечетное=нечетное, четное+четное=четное, нечетное+нечетное=четное.

Что ж, меньше слов, больше дела. Сделаем вывод немного нагляднее. Людям, не интересующимся программной реализацией следующий абзац будет неинтересен.

Я взял старый алгоритм расчета-вывода треугольника Паскаля и преобразовал его таким образом, что вместо значения чисел выводится остаток от его деления на 2. Стало быть, четные теперь стали нулями, нечетные — единицами. Сам код прилагаю ниже

Для пущей наглядности я разукрасил вывод следующим способом: вывод программы перенаправляется в файл, откуда по завершению выполнения первой, перл своими регэкспами заменяет единицы на красные буквы О, нули — на синие. Код скрипта ниже:

Из исходника видно, что смотреть мы будем html. Почему? Из соображений простоты. Только дерево DOM неверное получается. Исправим это скриптом на BASH и автоматизируем всё вышеописанное:

Итак, мы компилируем исходник на плюсах, его вывод уходит в текстовичок, баш «эхает» в html на перезапись началом дерева DOM, после чего текстовичок берет перл-скрипт, переделывает его в разноцветную html-версию, дополняет htmlку, после чего любезный БАШ снова завершает формирование дерева. Запускаем, смотрим:

Подчеркнем и сравним с оригиналом

PROFIT