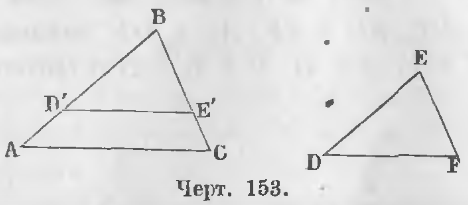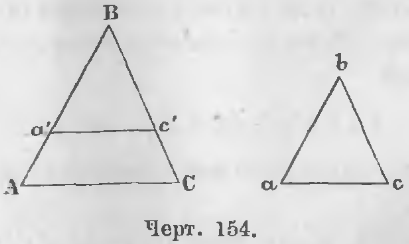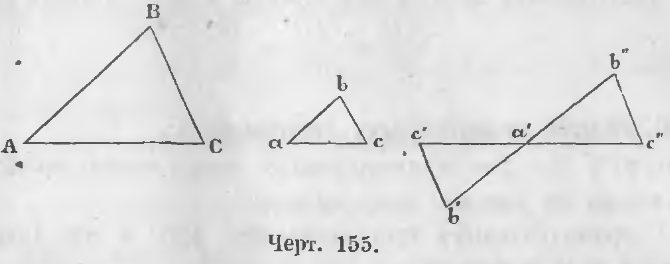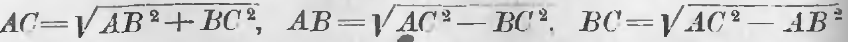Если стороны треугольников взаимно перпендикулярны

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Please wait.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

We are checking your browser. mathvox.ru

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d307cb938d616f0 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:№211. Плоскости правильного треугольника KDM и квадрата KMNP взаимно перпендикулярны. Найдите DN, есСкачать

Взаимно перпендикулярные стороны треугольника

Ключевые слова: треугольник, прямоугольный, катет, гипотенуза, теорема Пифагора, окружность

Треугольник называют прямоугольным, если у него есть прямой угол.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.

• По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
• Сумма двух острых углов прямоугольного треугольника равна прямому углу.
• Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
• Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
• Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = h_c из вершины С его прямого угла.

Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.

Все три треугольника АВС, АСD и ВСD подобны между собой.

Из подобия треугольников определяются соотношения:

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a 2 + b 2 = c 2

Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 ,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Признаки равенства прямоугольных треугольников:

• по катету и гипотенузе;
• по двум катетам;
• по катету и острому углу;
• по гипотенузе и острому углу.

См. также:
Площадь треугольника, Равнобедренный треугольник, Равносторонний треугольник

Видео:Треугольник с перпендикулярными медианами. Как найти третью сторону по известным двум?Скачать

Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180 0 .

Доказательство:

1 случай

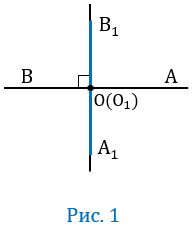
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁ и О₁В₁ также будут лежать на одной прямой, следовательно, А₁О₁В₁ — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

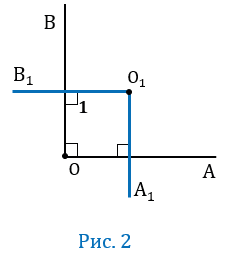
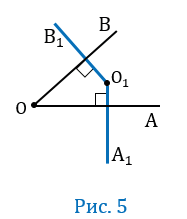
Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

АОВ = 90 0 , то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО₁А₁, тогда по теореме об односторонних углах их сумма равна 180 0 , т.е. 1 + А₁О₁В₁ = 180 0 , откуда А₁О₁В₁ = 180 0 —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т.е. 1 = 90 0 , следовательно, А₁О₁В₁ = 180 0 — 90 0 = 90 0 . Из равенств АОВ = 90 0 и А₁О₁В₁ = 90 0 следует, что АОВ = А₁О₁В₁ и АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

3 случай

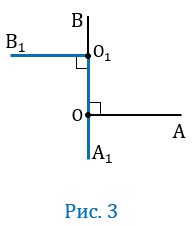
Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

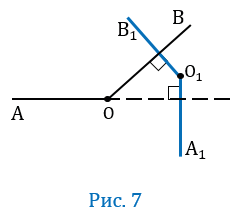
4 случай

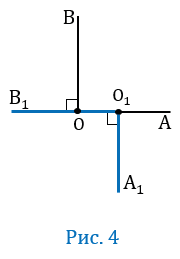
Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

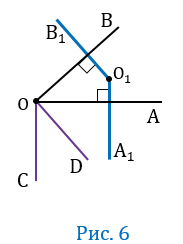
5 случай

Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90 0 — АОD, а СОD = 90 0 — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180 0 . Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180 0 .

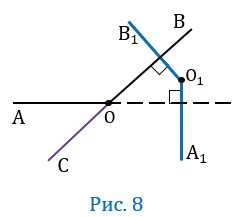
6 случай

Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180 0 , либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180 0 , значит АОС = 180 0 — АОВ, следовательно, в первом случае 180 0 — АОВ + А₁О₁В₁ = 180 0 , откуда АОВ = А₁О₁В₁, а во втором случае 180 0 — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180 0 . Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Видео:Боковые ребра треугольной пирамиды взаимно перпендикулярныСкачать

Математика

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

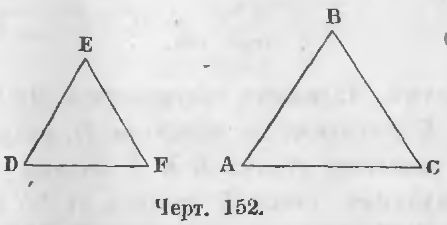
В треугольниках ABC и DEF (черт. 152), в которых

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

Видео:Геометрия 7 класс. Углы с соответственно параллельными или перпендикулярнымСкачать

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆ BD’E’ = ∆ DEF, следовательно,

Так как имеет место пропорция

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

Требуется доказать, что у них углы равны, т. е.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

a’b»c», следовательно, ∆ ABC

a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

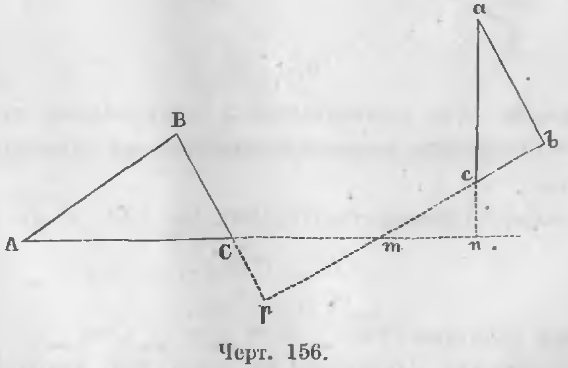
Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

∠pCm = ∠ACB, ∠mcn = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

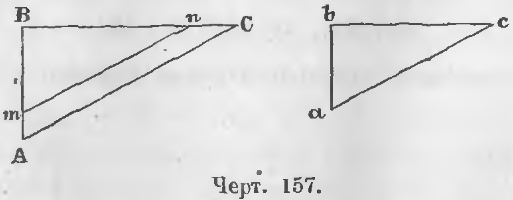
Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

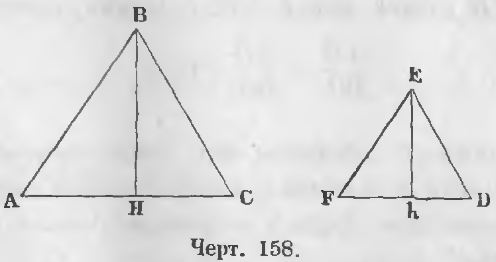
Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

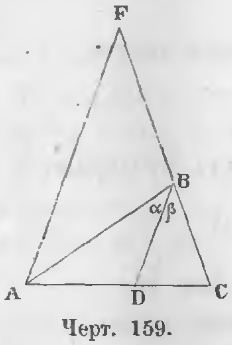
Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠ α = ∠ β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠ β как соответственные углы,
∠FAB = ∠ α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠ α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

Заменяя FB равным отрезком AB, получим пропорцию:

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

Требуется доказать, что ∠ α = ∠β .

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

Так как ∠ α = ∠ FAB, ∠β = ∠ AFB, то и

Видео:Перпендикулярные прямые. 6 класс.Скачать

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

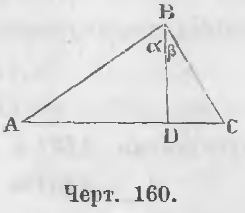
Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠ α = d, ∠ α + ∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α , которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ ABC = ∠ADB как прямые, ∠A общий, следовательно,

Из подобия треугольников вытекает пропорция:

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠ β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB 2 = AD · AC
BC 2 = DC · AC

Складывая их, получим:

AB 2 + BC 2 = AD · AC + DC · AC или
AB 2 + BC 2 = AC (AD + DC) = AC · AC = AC 2 , т. е.
AC 2 = AB 2 + BC 2

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC 2 = AB 2 + BC 2 .

Так как AB = BC, то AC 2 = 2AB 2 , откуда AC = AB √ 2 и AC/AB = √ 2 величина несоизмеримая.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

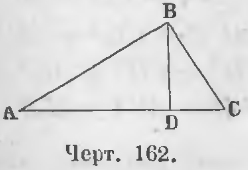
Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB 2 = BC 2 + AC 2 — 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB 2 = BD 2 + AD 2 (a)
AD = AC — DC, AD 2 = (AC — DC) 2 = AC 2 + DC 2 — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD 2 = BC 2 — DC 2

Вставляя величины BD 2 и AD 2 в равенство (a), получим:

AB 2 = BC 2 — DC 2 + AC 2 + DC 2 — 2AC · DC, откуда
AB 2 = BC 2 + AC 2 — 2AC · DC (ЧТД).

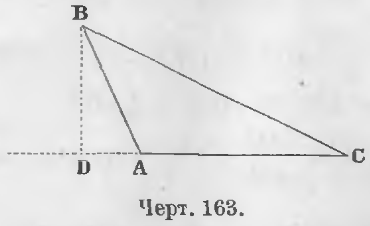
2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

Доказательство. Из прямоугольного треугольника ABD имеем:

AB 2 = BD 2 + DA 2

Из прямоугольного треугольника BCD имеем:

BD 2 = BC 2 — CD 2

AB 2 = BC 2 — CD 2 + DA 2 .

DA = CD — AC
DA 2 = (CD — AC) 2 = CD 2 + AC 2 — 2CD · AC, то
AB 2 = BC 2 — CD 2 + CD 2 + AC 2 — 2CD · AC, откуда
AB 2 = BC 2 + AC 2 — 2CD · AC (ЧТД).

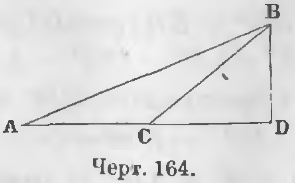
Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB 2 = AC 2 + BC 2 + 2AC · CD

Доказательство. Из тупоугольного треугольника ABC имеем:

AB 2 = BD 2 + AD 2 (a)
AD = AC + CD, AD 2 = AC 2 + CD 2 + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD 2 = BC 2 — CD 2

Заменяя AD 2 и BD 2 в равенстве (a), получим:

AB 2 = BC 2 — CD 2 + AC 2 + CD 2 + 2AC · CD

AB 2 = BC 2 + AC 2 + 2AC · CD (ЧТД).

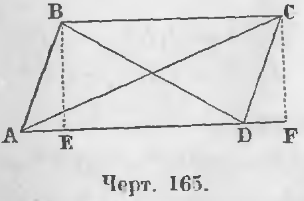
Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2

Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD 2 = AB 2 + AD 2 — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC 2 = CD 2 + AD 2 + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD 2 + AC 2 = AB 2 + AD 2 + CD 2 + AD 2

Так как AD = BC, то

BD 2 + AC 2 = AB 2 + BC 2 + CD 2 + AD 2 (ЧТД).

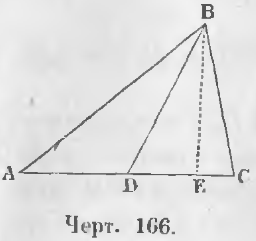
Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB 2 + BC 2 = 2AD 2 + 2BD 2

Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB 2 = BE 2 + AE 2
BC 2 = BE 2 + CE 2

Сложив их, находим:

AB 2 + BC 2 = 2BE 2 + AE 2 + CE 2 (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE 2 = (CD + DE) 2 = CD 2 + DE 2 + 2CD · DE
CE 2 = (CD — DE) 2 = CD 2 + DE 2 — 2CD · DE

AE 2 + CE 2 = 2CD 2 + 2DE 2 (b)

Заменяя в равенстве (a) сумму AE 2 + CE 2 из равенства (b), имеем:

AB 2 + BC 2 = 2BE 2 + 2CD 2 + 2DE 2 .

Из прямоугольного треугольника BDE видно, что

BE 2 = BD 2 — DE 2

AB 2 + BC 2 = 2BD 2 — 2DE 2 + 2CD 2 + 2DE 2

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Please wait.

Видео:Геометрия Задача № 25 ОГЭ 2021Скачать

We are checking your browser. mathvox.ru

Видео:Боковые ребра треугольной пирамиды взаимно перпендикулярныСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dc2759da89a7b63 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

🔥 Видео

Задание 13 (В1) ЕГЭ по математике (база) ▶ №13 (Минутка ЕГЭ)Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Геометрия Медианы AM и CK треугольника ABC перпендикулярны. Найдите стороны треугольникаСкачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Первый признак равенства треугольников. 7 класс.Скачать