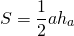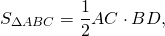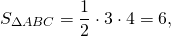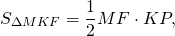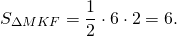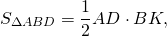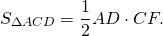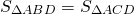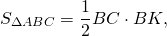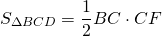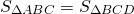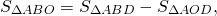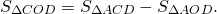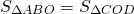Доказать что треугольники равновелики (8 видео)

Медиана делит площадь треугольника пополам

Два треугольника называются равновеликими. Если они имеют одинаковую площадь.

Теорема 1. Медиана делит треугольник на два равновеликих треугольника.

Пусть ВМ – медиана треугольника АВС. Докажем, что

Проведем высоту BH треугольника АВС. Тогда

Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому

Что и требовалось доказать.

Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.

Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».

Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.

Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.

Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, , К – точка пересечения медиан.

Так как треугольник АВК прямоугольный с прямым углом ВКА, то .

Так как медиан делят треугольник на 6 равновеликих частей, то .

Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.

Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.

Рассмотрим треугольник KAF.

то

Далее, , так как CKAE – параллелограмм (по признаку параллелограмма: ели диагонали четырехугольника делятся точкой пересечения пополам, до данный четырехугольник параллелограмм), получаем .

Так как , то есть , то по обратной теореме Пифагора (если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный) треугольник KAF – прямоугольный и .

Вычислим площадь треугольника AKF:

Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то

, ,

Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:

площадь треугольника, образованного медианами данного треугольника составляет от площади самого треугольника.

Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».

Вопросы для самопроверки:

1. Какие треугольники называются равновеликими?

2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?

3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?

4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?

5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?

6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?

Задачи для самостоятельного решения:

1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.

2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.

3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.

4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.

Содержание

Равновеликие фигуры
Презентация к уроку
Ход урока
I. Повторение.
II. Решение задач.
III. Изучение темы «Площадь треугольника»
IV. Шаг вперёд!
V. Задача дня.
Равновеликие треугольники
🎥 Видео

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Равновеликие фигуры

Презентация к уроку

Загрузить презентацию (299 кБ)

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

начать с задачи:

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

Равновелики ли равные фигуры?
Сформулируйте обратное утверждение. Верно ли оно?
Верно ли:
а) Равносторонние треугольники равновелики?
б) Равносторонние треугольники с равными сторонами равновелики?
в) Квадраты с равными сторонами равновелики?
г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы:

Учебник «Геометрия 7-9» (авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
Подборка задач, накопленных за много лет работы.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Равновеликие треугольники

Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.

Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.

Например, треугольники ABC и MKF — равновеликие, так как их площади равны.

Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.

Равновеликие треугольники в треугольнике

Медиана делит треугольник на два равновеликих треугольника.

Равновеликие треугольники в трапеции

При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:

1) ∆ABD и ∆ACD,