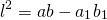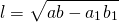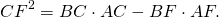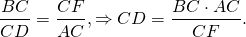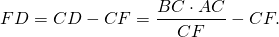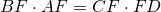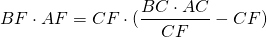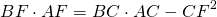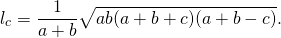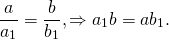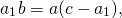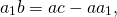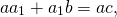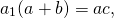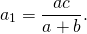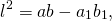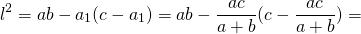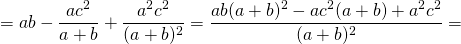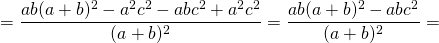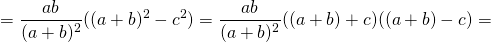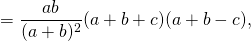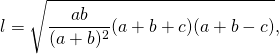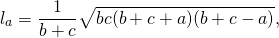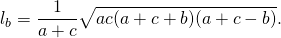Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
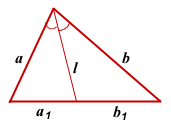
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
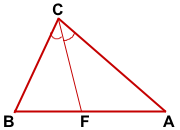
СF — биссектриса ∠ABC
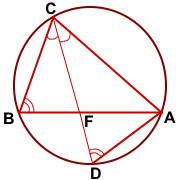
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.
Рассмотрим треугольники BCF и DCA.
∠BCF=∠DCA (по условию);
Значит, треугольники BFC и DCA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Что и требовалось доказать.
II. Через три стороны треугольника
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле
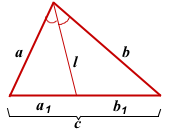
Согласно утверждению 1,
Что и требовалось доказать.
III Через две стороны треугольника и угол между ними.
Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле
Видео:Формула для биссектрисы треугольникаСкачать

Все формулы биссектрисы в треугольнике
L — биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p =(a+b+ c )/2
Длина биссектрисы через две стороны и угол, ( L ):
Длина биссектрисы через полупериметр и стороны, ( L ):
Длина биссектрисы через три стороны, ( L ):
Длина биссектрисы через стороны и отрезки d , e , ( L ):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Биссектриса треугольника онлайн
С помощю этого онлайн калькулятора можно найти биссектрису треугольника. Для нахождения длины биссектрисы треугольника введите длины сторон треугольника, выберите сторону, к которой проведена биссектриса и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Определение 1. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника (Рис.1).
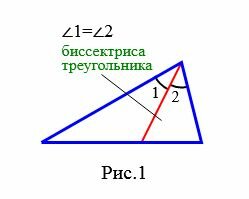 |
Биссектриса треугольника также называют биссектрисей угла треугольника или биссектрисей внутреннего угла треугольника.
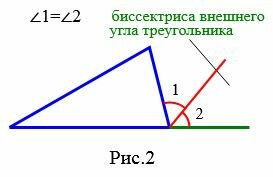
Биссектриса внешнего угла треугольника − это биссектриса угла, которая является смежным с внутренним углом треугольника (Рис.2).
 |
Любой треугольник имеет три биссектрисы.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке.
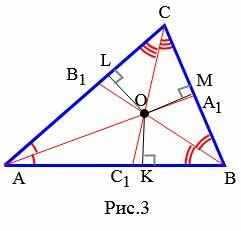 |
Доказательство. Проведем биссектрисы AA1, BB1 и обозначим через O точку их пересечения (Рис.3). Из точки O проведем перпендикуляры OK, OM и OL по сторонам треугольника ABC. По теореме 1 статьи Биссектриса угла. Свойства − OK=OL OK=OM. Следовательно OL=OM. Но последнее равенство означает, что точка O равноудалена от сторон AC и BC, т.е. находится на биссектрисе CC1 (Определение 2 статьи Биссектриса угла. Свойства).
Точка пересечения биссектрис треугольника называется инцентром треугольника. Инцентр треугольника является центром вписанной в треугольник окружности (Рис.4).
 |
Доказательство следует из теоремы 1, поскольку точка O равноудалена от сторон треугольника ABC и, следовательно, является центром окружности равной OK=OL=OM.
Видео:Найдите биссектрису треугольникаСкачать
Длина биссектрисы треугольника
Рассмотрим треугольник на Рис.5.
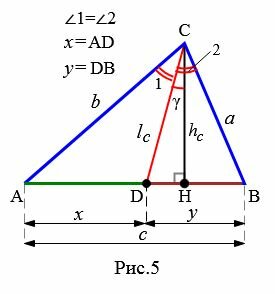 |
Длина биссектрисы треугольника можно вычислить следующими формулами:
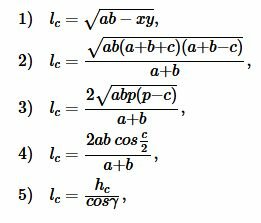 |
где p − полупериметр треугольника ABC, ( small gamma -) угол между биссектрисой ( small l_c) и вершиной ( small h_c:)
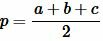 , , 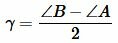 |
Доказательство. 1) Из теоремы Стюарта следует:
 | (1) |
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
 | (2) |
Поскольку 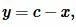
 | (3) |
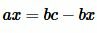 |
 | (4) |
 |
 | (5) |
Подставим (4) и (5) в (1):
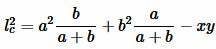  |
 . . | (6) |
 . . |
Доказательство. 2) Подставим (4) и (5) в (6):
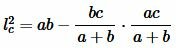 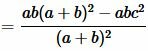 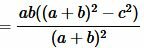 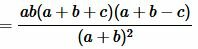 , , |
 . . | (7) |
 . . | (8) |
Доказательство. 3) Сделаем следующее обозначение:
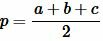 . . | (9) |
Сделаем преобразования формулы (7), учитывая (9):
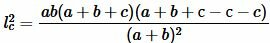 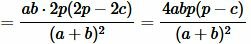 . . |
 . . | (10) |
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
 , , |
 , , |
 . . |
Учитывая, что 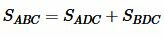
 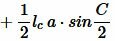 |
 . . |
 . . | (11) |
Для ( small sin C ) применим формулу синуса двойного угла:
 . . | (12) |
Подставляя (12) в (11) получим:
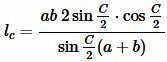 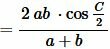 . . |
 . . | (13) |
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
 . . |
 . . |
Остается показать, что 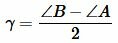
Поскольку биссектриса lc делит угол C пополам, то:
🔥 Видео
Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

ОГЭ 16🔴Скачать

Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать

Биссектрисы треугольника.Скачать

№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

Построение биссектрисы углаСкачать

Задание 9 ОГЭ от ФИПИСкачать

Свойства биссектрисы треугольникаСкачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Построение биссектрисы в треугольникеСкачать

Биссектриса треугольника. Построение. 1 частьСкачать

Cекретное свойство биссектрисыСкачать

Построение биссектрисы угла. 7 класс.Скачать

11 класс, 46 урок, Теорема о биссектрисе треугольникаСкачать