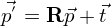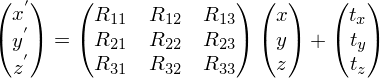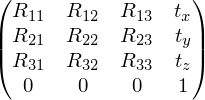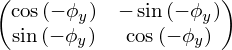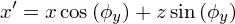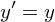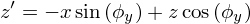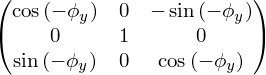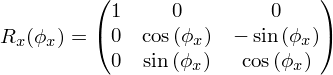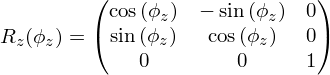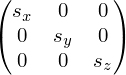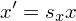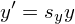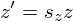Скорее всего, каждый из Вас хоть раз в жизни слышал термин «аффинные преобразования». Действительно, все постоянно о них говорят: «инвариантность к аффинным преобразованиям», «аугментация с помощью аффинных преобразований», «аффинные преобразования в компьютерной графике» и так далее. Однако, далеко не все могут сходу ответить на простой вопрос: «А расскажите, что такое аффинные преобразования простыми словами».
Вы сможете? В любом случае, давайте немного обсудим этот вопрос.
- Что такое аффинное преобразование?
- Примеры аффинных преобразований
- Поворот
- Растяжение-сжатие
- Сдвиг
- Эпилог
- Решение задач с помощью аффинных преобразований
- Аффинные преобразования поворот треугольника
- Друзья
- Аффинные преобразования пространства
- Параллельный перенос
- Поворот (вращение)
- Поворот вокруг оси y
- Поворот вокруг осей x и z
- Масштабирование (сжатие/растяжение, отражение)
- Интерпретация матрицы R
- Сложные аффинные преобразования
- 📸 Видео
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Что такое аффинное преобразование?
Начнем с классики — определение из Википедии.
Аффинное преобразование (от лат. affinis «соприкасающийся, близкий, смежный») — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.
Внесем немного ясности.
Во-первых, что значит «отображение в себя»? Это значит, что если мы находились в пространстве , то после образования мы должны остаться в нем же. Например: если мы применили какое-то преобразование к прямоугольнику и получили параллелепипед, то мы вышли из
в
. А вот если из прямоугольника у нас получился другой прямоугольник, то все хорошо, мы отобразили исходное пространство в себя. Формально это описывается так: «преобразование
отображает пространство
в
». Если записать с помощью формул:
.
Во-вторых, что такое «скрещивающиеся прямые»? Конечно, все это проходили в школе, но на всякий случай напомним. Прямые называются скрещивающимися, если они не лежат в одной плоскости. Вот если бы они лежали в одной плоскости и пересекались, они назывались бы пересекающимися. А если в разных плоскостях, то скрещивающимися. Пример — на рисунке.
В целом, это определение уже нам что-то говорит и мы начинаем потихоньку рисовать для себя картинку. Как минимум, мы должны остаться в той же плоскости: значит мы представляем себе декартову систему координат. Здесь речь идет о нескольких прямых, так что давайте представим 2 параллельных линии. Из определения мы понимаем, что после преобразования эти линии должны остаться параллельными. Ну что ж, тогда просто сдвигаем их куда-нибудь из исходного местоположения, да и все.
По сути, мы с Вами только что описали один из видов аффинных преобразований — сдвиг.
Но давайте пойдем чуть дальше и дадим еще одно определение (не нами придуманное).
Преобразование плоскости называется аффинным, если оно непрерывно, взаимно однозначно и образом любой прямой является прямая.
Звучит это, пожалуй, чуть сложней и путанней, но дает нам больше конкретной информации, чем предыдущее определение.
Преобразование называется непрерывным, если «близкие точки переходят в близкие». Т.е. иначе — если у нас есть две точки и они находятся рядом, то после преобразования они все равно будут находиться где-то поблизости друг от друга.
Далее — преобразование взаимооднозначно, если разные точки переводятся в разные точки и в каждую точку переводится какая-то точка. Например: если мы отобразили отрезок и он слипся в точку — это не взаимооднозначное преобразование. Из отрезка мы должны получить ровно такой же отрезок, тогда будет взаимооднозначно (если это сработает для всех отрезков, конечно).
Итак, с определениями мы разобрались. Давайте теперь запишем в общем виде, а как выглядит преобразование координат в формульном виде.
Пусть у нас есть исходная система координат. Точка в этой системе характеризуется двумя числами — и
. Совершить переход к новым координатам
и
мы можем с помощью следующей системы:
При этом, числа должны образовывать невырожденную матрицу:
На всякий случай: матрица называется невырожденной, если ее определитель не равен нулю, т.е.
Можно записать и в более общем в виде.
Аффинное преобразование — преобразование вида
, где
— обратимая матрица, а
. В данном случае
, само собой,
-мерный вектор.
Видео:Видеоурок "Преобразование координат"Скачать

Примеры аффинных преобразований
Мы с Вами достаточно подробно разобрали, что такое аффинное преобразование и как его можно описать с помощью формул. Давайте теперь рассмотрим популярные примеры.
Приходят ли Вам в голову какие-нибудь претенденты на роль? Позвольте мы внесем свои предложения.
Поворот
Пусть .
Значит, матрица примет вид:
И новые координаты будут выглядеть так:
Ничего не напоминает? Если Вы еще не узнали, то встречайте — это просто повернутая система координат на угол . Т.е. мы применили аффинное преобразование и наша система координат повернулась. Пример этого Вы можете видеть на графике.
Растяжение-сжатие
Теперь мы предлагаем сконструировать матрицу несколько иначе:
Новые координаты тогда принимают вид:
В целом, тут даже уже из вида системы уравнений понятно, что мы просто растягиваем наши оси, если коэффициент меньше 1 и сжимаем, если больше 1. Пример на рисунке.
Кстати говоря, а попробуйте поставить вместо число -1, а вместо
просто 1. Что получится? Правильно, мы просто отразим нашу систему координат относительно оси
.
Сдвиг
Ну и давайте напоследок еще один пример.
Пусть теперь матрица никак не меняет исходные координаты (т.е.
). А вот
пусть равняется
, а
.
Таким образом, наша система принимает вид:
Если отразить это на графике, то мы просто сдвинули начало координат в точку . Вот, собственно, и вся премудрость.
Видео:OpenGL - Урок 3 - Матрица преобразований. Перемещение, вращение, масштаб.Скачать

Эпилог
Эта короткая статья позволит Вам чуть сильней прочувствовать «внутренности» аффинных преобразований (мы надеемся на это). После прочтения попробуйте все-таки ответить на вопрос, который мы ставили в самом начале — «А расскажите, что такое аффинные преобразования простыми словами». Теперь сможете?
P.S. Кстати говоря, было бы неплохо не верить нам на слово и проверить самим — а матрицы , которые мы использовали — точно невырожденные? Может мы вообще что-то противозаконное сделали.
Видео:Семинар №12 "Аффинные преобразования плоскости"Скачать

Решение задач с помощью аффинных преобразований
Разделы: Математика
Для начала: на чем основывается метод решения с помощью аффинных преобразований?
Необходим некий краткий теоретический материал для учащихся.
Сообщаем, что система координат не обязательно должна быть прямоугольной. Если выбрать на плоскости 3 точки 



Сообщаем, что система координат не обязательно должна быть прямоугольной. Если выбрать на плоскости 3 точки 



Определение 1. Пусть в плоскостях 













Свойства аффинных преобразований:
1) По свойствам координат аффинное преобразование является взаимно однозначным отображением плоскости на плоскость:
— каждая точка имеет образ и притом только один;
— разные точки имеют разные образы;
— каждая точка области значений имеет прообраз.
2) Так как аффинное отображение сохраняет координаты точек, то оно сохраняет уравнения фигур. Отсюда следует, что прямая переходит в прямую.
3) Преобразование, обратное к аффинному, есть снова аффинное преобразование.
4) Точки, не лежащие на одной прямой, переходят в точки, не лежащие на одной прямой, а, значит, пересекающиеся прямые — в пересекающиеся прямые, а параллельные – в параллельные.
5) При аффинных преобразованиях сохраняются отношения длин отрезков, лежащих на одной или параллельных прямых.
6) Отношения площадей многоугольников также сохраняются.
7) Не обязательно сохраняются отношения длин отрезков непараллельных прямых, углы.
Замечание 1: Если А, В, С — три точки плоскости, не лежащие на одной прямой, а 

Замечание 2: Параллельное проектирование есть аффинное преобразование плоскости на плоскость. Кстати эта тема “Параллельное проектирование” присутствует в школьном учебнике геометрии 10-11(2000) Л. С. Атанасяна в приложении 1. В основном этот материал используется тогда, когда мы учим изображать пространственные фигуры на плоскости.
Чтобы представить, что могут аффинные преобразования, посмотрим картинки. Учащимся лучше всего именно наглядно показать применение аффинных преобразований на отвлеченном предмете и только потом переходить на геометрические фигуры.
Частным случаем аффинных преобразований являются преобразование подобия, гомотетия и движения. Движения — это параллельные переносы, повороты, различные симметрии и их комбинации. Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой. На рисунке 2 показаны различные движения плоскости с нарисованным на ней домиком. А на рисунке 3 и 4 показаны различные аффинные преобразования этой плоскости (параллельное проектирование).
А вот на следующей картинке можно объяснить суть метода.
Если перед вами стоит задача о вычислении каких-то соотношений или пропорций на искаженном рисунке, например: найти отношение длины ушей к длине хвоста, то можно найти это отношение на более удобном рисунке (неискаженном), что намного проще, и найденное решение будет соответствовать и искаженному рисунку в том числе. Но нельзя искать отношение, например, длины ушей к толщине зайца, т.к. это отрезки непараллельных прямых.
Теперь перейдем к геометрическим фигурам. Как на них может работать этот метод?
Обычно, задачу можно решить методом аффинных преобразований, если нужно найти отношение длин, отношение площадей, доказать параллельность или принадлежность точек одной прямой. Причем в условии задачи не должны содержаться данные, не сохраняющиеся при аффинных преобразованиях.
Свойства фигур называются аффинными, если они сохраняются при аффинных отображениях. Например, быть медианой треугольника- это аффинное свойство (середина стороны переходит в середину при аффинном отображении), а быть биссектрисой – нет.
Суть метода при решении геометрических задач.
Часто бывает удобно при решении задач на аффинные свойства перейти с помощью аффинных преобразований к более простым фигурам, например, к правильному треугольнику. А затем с помощью обратного аффинного преобразования перенести полученный результат на искомую фигуру.
Для начала можно решить всем известную задачу о точке пересечения медиан треугольника.
Задача 1. Доказать, что медианы произвольного треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины.
Решение (по алгоритму).
Пусть дан треугольник ABC. 1) Проверим аффинные свойства фигуры. Треугольник (по замечанию 1) является аффинной фигурой, быть медианой — это тоже аффинное свойство и отношения длин отрезков также сохраняется при аффинном отображении.
2) Значит, можно перейти к более удобной фигуре — равностороннему треугольнику.
3) Возьмем равносторонний треугольник 






4) Зададим аффинное отображение, переводящее треугольник 

5) Утверждение для произвольного треугольника доказано.
Задача 2. Доказать, что в любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
Пусть дана трапеция ABCD, в которой M и N – середины оснований, Q – точка пересечения диагоналей, О – точка пересечения продолжений боковых сторон.
1) Проверим аффинные свойства фигуры. Трапеция — аффинная фигура (так как трапеция переходит в трапецию), принадлежность точек одной прямой является аффинным свойством. Таким образом, и условие, и вопрос задачи относятся к аффинному классу задач. Значит, можно применить метод аффинных преобразований.
2) Возьмем произвольный равнобедренный треугольник 








3) Доказать сформулированную задачу для равнобокой трапеции труда не составит (при чем не одним способом).
4) Таким образом, доказав, что точки 



5) Доказанный факт справедлив и для произвольной трапеции.
Примечание. Четырехугольники аффинно эквивалентны тогда и только тогда, когда точка пересечения диагоналей делит их в одном и том же отношении.
Задача 3 (из диагностической работы по подготовке к ЕГЭ-2010). Через точку О, лежащую в треугольнике АВС, проведены три прямые, параллельные всем сторонам треугольника. В результате треугольник разбился на 3 треугольника и 3 параллелограмма. Известно, что площади полученных треугольников равны соответственно 1; 2.25 и 4. Найдите сумму площадей полученных параллелограммов (задача из диагностической работы по подготовке к ЕГЭ — 2010)
Решение, предложенное авторами
Но эту задачу легко решить с помощью аффинных преобразований.
- Проверим аффинные свойства фигуры. Треугольник является аффинной фигурой, параллельность также относится к аффинным свойствам. Так как известны площади, можно найти их отношение, которое будет сохраняться при аффинных преобразованиях.
- Пусть даны два треугольника: произвольный и равносторонний. Решить задачу на равностороннем треугольнике намного проще. Возьмем аффинное отображение, переводящее произвольный треугольник в равносторонний.
- Решаем задачу на равностороннем.
Треугольники, получившиеся внутри нашего равностороннего, являются подобными (по 2 углам). Следовательно, их площади относятся как квадрат коэффициента подобия, обозначим 







По свойствам аффинных отображений решение справедливо и для произвольного треугольника.
Мы рассмотрели планиметрические задачи, но свойства аффинных преобразований работают и в пространстве. Например, образом тетраэдра может служить произвольный заранее выбранный тетраэдр. У любого параллелепипеда аффинным образом может быть куб.
Задача 4 (стереометрическая). Докажите, что диагональ 



Это №372 из учебника Атанасяна (11 класс). В учебнике дано ее решение векторным методом. Но можно применить метод аффинных преобразований, решив эту задачу на кубе уже в 10 классе.
В этой задаче с помощью аффинных преобразований докажем равенство трех отрезков.
1) Проверим аффинные свойства фигуры и условия задачи. Аффинным образом любого параллелепипеда может быть куб. Деление отрезка в заданном отношении – это аффинное свойство.
2) Рассмотрим одноименный куб 



3) Докажем, что диагональ делится этими точками на три равных отрезка.
1. Рассмотрим пирамиду 





















2. Аналогично найдем 


3. Из треугольника 


4. Вычислим 




5. Получили 





4) Существует аффинное отображение, переводящее куб в произвольный параллелепипед. Значит, эта задача будет верна и для произвольного параллелепипеда.
5) Обобщения. Какие свойства, доказанные на кубе, сохранятся для произвольного параллелепипеда, а какие нет (обсудить с учащимися).
Например: параллельность плоскостей и отношение сохранится, перпендикулярность диагонали плоскостям нет, правильные треугольники не сохранятся, так же как и центр правильного треугольника, он перейдет в точку пересечения медиан.
Таким образом, уже в 10 классе можно делать с учащимися обобщения для произвольных фигур, пользуясь свойствами аффинных отображений.
Мы рассмотрели задачи программного уровня, а теперь рассмотрим задачи продвинутого уровня.
Вот задача, предложенная учащимся 11-го класса на олимпиаде в этом году. Никто, к сожалению, с ней не справился. Посмотрим, как метод аффинных преобразований поможет нам ее решить.
Задача 5 (олимпиада 11 класс). Треугольная пирамида рассечена плоскостью так, что медианы боковых граней разбиты точками пересечения в отношении 2:1,3:1 и 4:1, считая от вершины пирамиды. В каком отношении, считая от вершины пирамиды, разбиты боковые рёбра? (Из материалов МГТУ им. Баумана). Ответ: 12:7 , 12:5, 12:1
Существует решение, предложенное авторами. В этом решении отсутствуют различные подробные вычисления, поэтому по объему решение недлинное, о сложности будете судить сами.
А решение с помощью аффинных преобразований мы рассмотрим.
1) В задаче фигурирует произвольная пирамида, в которой проведены медианы (а быть медианой — это аффинное свойство), на медианах взяты пропорциональные отрезки ( при аффинном преобразовании сохраняются отношения длин отрезков, лежащих на одной прямой). Значит, эту задачу можно решить для “удобной” пирамиды, а затем с помощью аффинного преобразования перенести результат на произвольную.
2) Решим задачу для пирамиды, у которой три плоских угла при вершине прямые. Поместим новую пирамиду в прямоугольную систему координат OXYZ.
3) Проведем медиану 
















Итак: К


N 
Анализируя, выберем сами удобные числовые координаты для точек А(40;0;0), В(0;15;0), С(0;0;24).
Плоскость (MNK) пересекает ребра пирамиды в неких точках 
















Нам надо найти отношение 

Решив задачу на “удобной” пирамиде, учитывая, что существует аффинное преобразование, переводящее эту пирамиду в произвольную, переносим результат на произвольную пирамиду.
Если бы в условии данной задачи была предложена “удобная” пирамида, наверное, кто-то из учеников сделал хотя бы попытки решить задачу.Метод аффинных преобразований позволяет трудные факты свести к легкому доказательству.
Например, доказать следующую задачу 6: Пусть заданы два треугольника АВС и 
Любой четырехугольник может рассматриваться, как образ тетраэдра при параллельной проекции на плоскость. Рассмотрим четырехугольник SABС.
Существует аффинное преобразование f, переводящее его в четырехугольник 








Построение.1) 

В пересечении плоскостей три точки, следовательно, они лежат на одной прямой. Эта задача (теорема Дезарга) доказана.
В продолжение такого применения аффинных преобразований (решение пространственной задачи как планиметрической) можно рассмотреть еще одну интересную задачу.
Задача (Соросовская олимпиада)
Даны три луча 
То есть картинка должна быть примерно такая.
Будем рассматривать эту картинку как аффинный образ (при некотором аффинном отображении) пирамиды XOYZ на плоскость. Вершины пирамиды лежат на осях координат, а точки А, В, С — точки в координатных плоскостях. Тогда задача сводится к тому, чтобы построить линии пересечения плоскости (АВС) с координатными плоскостями. Существует, конечно, способ построения с помощью циркуля и линейки, но нам он не нужен. Итак, без циркуля.
- Возьмем произвольную точку S на луче
.
- Проведем прямые
и
.
,
.
, такая, что Р и С лежат в одной плоскости.
,
- ZY,
- XYZ — искомый треугольник.
Выводы.
Итак, вам был представлен метод решения задач с помощью аффинных преобразований. Подведем итоги.
- Метод позволяет перейти от более сложного к более простому для осуществления процесса решения.
- Носит обобщающий характер.
- Имеет широкую область применения, в том числе в смежных областях.
- Позволяет интегрировать разные разделы математики.
- Осмысление и применение данного метода формирует у учащихся конструктивный подход к решению задач и критичность мышления.
Видео:Построение натуральной величины треугольника методом вращенияСкачать

Аффинные преобразования поворот треугольника
Друзья
Аффинные преобразования пространства
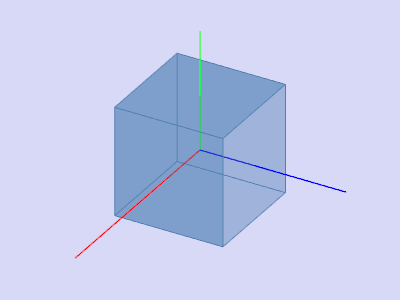
При работе с трехмерными объектами, часто требуется совершать по отношению к ним различные преобразования: двигать, поворачивать, сжимать, растягивать, скашивать и т.д. При этом в большинстве случаев требуется, чтобы после применения этих преобразований сохранялись определенные свойства.
Определение. Преобразование плоскости называется аффинным (от англ. affinity – родство) , если
- оно взаимно однозначно;
- образом любой прямой является прямая.
Преобразование называется взаимно однозначным, если
- разные точки переходят в разные;
- в каждую точку переходит какая-то точка.
Свойства аффинного преобразования в трехмерном пространстве:
- отображает n -мерный объект в n -мерный: точку в точку, линию в линию, поверхность в поверхность;
- сохраняет параллельность линий и плоскостей;
- сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.
Любое аффинное преобразование задается матрицей 3 x 3 с ненулевым определителем и вектором переноса:
Посмотрим на это с точки зрения математики. R представляет собой матрицу линейного оператора над пространством трехмерных векторов. Вектор T требуется для осуществления параллельного переноса: если помножить ( 0 0 0 ) на любую матрицу 3 x 3, опять получим ( 0 0 0 ) – начало системы координат, относительно преобразования R , является неподвижно точкой. Требование, чтобы определитель был ненулевой, диктуется определением. По сути, если определитель матрицы R равен нулю, то всё пространство переходит в плоскость, прямую или точку. Тем самым не соблюдается взаимная однозначность.
На практике удобно задавать аффинное преобразование одной матрицей. При этом используются однородные координаты, введенные в предыдущей статье. Аффинное преобразование будет задаваться следующей матрицей 4 x 4:
Заметим, что первые три значения последней строки равны 0. Это необходимое условие того, что преобразование будет аффинным. В общем случае произвольная матрица размера 4 x 4 задает проективное преобразование. Такие преобразования, как можно догадаться из названия, используются для проецирования трехмерной сцены. Подробнее об этом будет рассказано в одной из последующих статей.
Рассмотрим частные случаи аффинных преобразований.
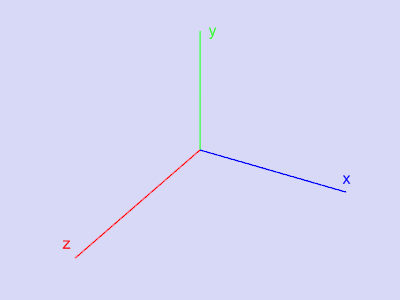
Прим. Здесь и в дальнейшем будет использоваться система координат, введенная следующим образом:
- система координат правая ;
- ось z направлена на наблюдателя, перпендикулярно плоскости экрана;
- ось y находится в плоскости экрана и направлена вверх;
- ось x находится в плоскости экрана и направлена вправо.
Подробнее мы остановимся на этом при рассмотрении геометрического конвейера.
Параллельный перенос
 | 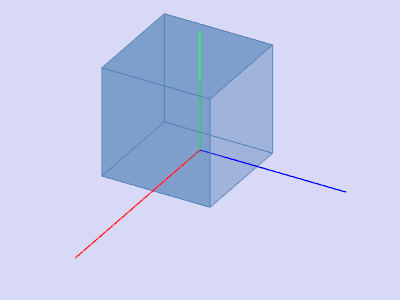 | ||||||||
 | 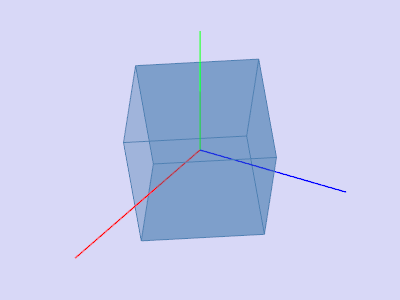 | ||||||
 | 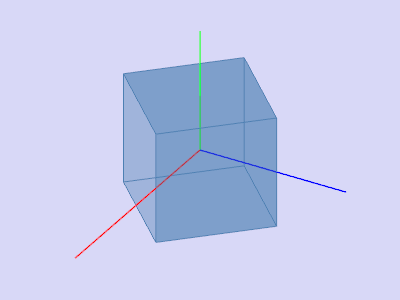 | ||||
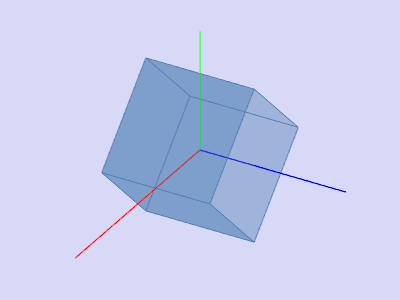 |  | ||
 |  |
 |  |






















 .
. и
и  .
. ,
,  .
. , такая, что Р и С лежат в одной плоскости.
, такая, что Р и С лежат в одной плоскости. ,
,