24 грани из треугольников

Формулы и виды симметрии:

1) 3L₄ 4L₃ 6L₂ 9PC – планальный вид симметрии;

Простые формы: в кубической сингонии существует 5 основных простых форм и 10 производных.

Основные простые формы(рис.4.1-4.15):

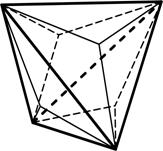
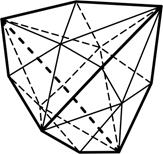
1) кубический тетраэдр – 4 равные грани в форме правильного треугольника, из которого каждые 3 грани пересекаются в одной точке (рис.4.1);

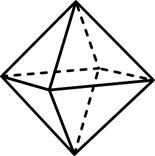
2) октаэдр – 8 граней в форме правильных треугольников (рис.4.2);

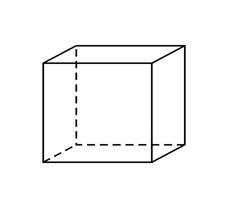
3) гексаэдр (куб) – 6 граней в форме квадратов (рис.4.3);

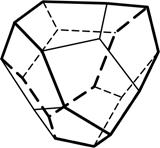
4) ромбо-додекаэдр – 12 граней в форме ромбов (рис.4.4);

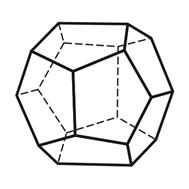
5) пентагон-додекаэдр – 12 граней в форме пятиугольников (рис.4.5).

Производные простые формы:

из кубического тетраэдра образуются следующие производные:

6) тригон-тритетраэдр – состоит из 12 граней в форме равнобедренных треугольников, образуется путём расщепления каждой грани тетраэдра на 3 треугольные грани следующим образом (рис.4.6);

7) тетрагон-тритетраэдр – 12 граней в форме четырёхугольников, образуется посредством утроения каждой грани тетраэдра следующим образом (рис.4.7);

8) пентагон-тритетраэдр – 12 граней в форме пятиугольников (рис. 4.8);

9) гексатетраэдр – 24 грани в форме треугольников, образуется посредством ушестерения каждой грани тетраэдра (рис.4.9).

Все производные от тетраэдра в первом приближении похожи на тетраэдр.

Из октаэдра аналогичным способом образуются следующие производные:

10) тригон-триоктаэдр – 24 грани в форме равнобедренных треугольников (рис.4.10);

11) тетрагон-триоктаэдр – 24 грани в форме четырёхугольников (рис.4.11);

12) пентагон-триоктаэдр – 24 грани в форме пятиугольников (рис.4.12);

13) гексоктаэдр – 48 граней в форме разносторонних треугольников (самая большая простая форма по количеству граней) (рис.4.13);

Из гексаэдра образуется одна производная форма:

14) тетрагексаэдр – 24 грани в форме равнобедренных треугольников, образуется посредством учетверения каждой грани гексаэдра (рис.4.14).

Из пентагон-додекэдра образуется одна производная:

15) дидодекаэдр – 24 грани в форме четырёхугольников, образуется посредством удвоения каждой грани пентагон-додекаэдра (рис.4.15).

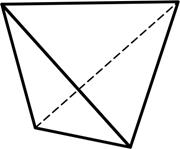
Тетраэдр Октаэдр Гексаэдр (куб)

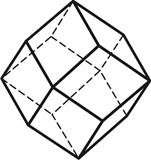
Ромбо-додекаэдр Пентагон-додекаэдр Тригон-тритетраэдр

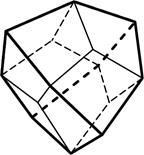
Тетрагон-тритетраэдр Гексатетраэдр Пентагон-тритетраэдр

Рис. 4. Простые формы кубической сингонии

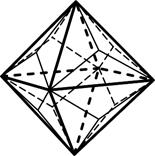
Тригон-триоктаэдр Тетрагон-триоктаэдр Гексоктаэдр

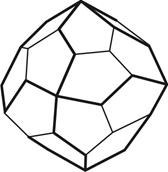
Пентагон-триоктаэдр Тетрагексаэдр Дидодекаэдр

Рис. 4. Простые формы высшей категории сингонии (окончание)

Принцип наименованияпростых форм кубической сингонии заключается в следующем. В сложных названиях первое слово означает форму грани (тригон – треугольник, тетрагон – четырёхугольник, пентагон – пятиугольник). Второе слово – количество граней в простой форме.

При указании количества граней используют следующие греческие числительные:

ди – 2; три – 3; тетра – 4; гекса – 6; окта – 8; додека – 12,

при этом 12-гранники называются по разному: додекаэдр и тритетраэдр (три – 3, тетра – 4, 3Х4 = 12). Различие в том, что тритетраэдр является производной формой и корень этого слова даёт указание, из какой основной формы она образована (из тетраэдра). Поэтому 24-гранники называются также неодинаково: триоктаэдр, гексатетрадр, дидодекаэдр, тетрагексаэдр.

Все 15 простых форм кубической сингонии являются закрытыми.

Хромой цилиндр в геометрии курносый куб

Курносый куб

• Курно́сый куб, или плосконо́сый куб, — полуправильный многогранник (архимедово тело) с 38 гранями, составленный из 6 квадратов и 32 правильных треугольников. В каждой из его 24 одинаковых вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными.

Имеет 60 рёбер равной длины.

Название «курносый куб» (лат. cubus simus) дал этому многограннику Иоганн Кеплер в трактате 1619 года «Гармония мира». Гарольд Коксетер, отметив, что многогранник родствен октаэдру в той же мере, что и кубу, предлагал называть его «курносым кубооктаэдром».

В отличие от большинства других архимедовых тел, курносый куб (наряду с курносым додекаэдром) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «левом» и «правом».

Связанные понятия

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Пра́вильный пятияче́йник, или просто пятияче́йник, или пентахор (от др.-греч. πέντε — «пять» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве: правильный четырёхмерный симплекс.

В теории чисел квадратным треугольным числом (или треугольным квадратным числом) называется число, являющееся как треугольным, так и квадратным.

Курносый куб

Из Википедии — свободной энциклопедии

«Левый» вариант
(вращающаяся модель, 3D-модель)Типархимедово телоСвойствавыпуклый, изогональный, хиральныйКомбинаторикаЭлементы

38 граней 60 рёбер 24 вершины

Χ = 2

Грани32 треугольника,
6 квадратовКонфигурация вершины3 4 .4Двойственный многогранникпентагональный икоситетраэдр

Курно́сый куб [1] , или плосконо́сый куб [2] [3] , — полуправильный многогранник (архимедово тело) с 38 гранями, составленный из 6 квадратов и 32 правильных треугольников. В каждой из его 24 одинаковых вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными.

Имеет 60 рёбер равной длины.

Название «курносый куб» (лат. cubus simus ) дал этому многограннику Иоганн Кеплер в трактате 1619 года «Гармония мира». Гарольд Коксетер, отметив, что многогранник родствен октаэдру в той же мере, что и кубу, предлагал называть его «курносым кубооктаэдром».

В отличие от большинства других архимедовых тел, курносый куб (наряду с курносым додекаэдром) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».

Курносый куб

Упражнение 12. Имеет ли центр симметрии: а) курносый куб; б) курносый додекаэдр? Ответ: а) Нет; Б) нет.

Слайд 16 из презентации «Задания на симметрию» к урокам геометрии на тему «Симметрия»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Задания на симметрию.ppt» можно в zip-архиве размером 492 КБ.

Симметрия

«Виды симметрии в геометрии» — Фигуры, обладающие центральной и осевой симметрией. Осевая симметрия. Прямая, содержащая биссектрису равнобедренного треугольника. Цель урока. Человек веками пытается объяснить и создать порядок. Симметрия. Практическая работа. Центральная симметрия фигур. Зеркальная симметрия. Определить фигуры. На зеркальной поверхности сидит мотылек.

«Симметрия вокруг нас» — Симметрия в пространстве. Симметрия властвует. Симметрия. В геометрии есть фигуры, которые имеют. Осевая. Вращения. Вертикальная. Один вид симметрии. Все виды осевой симметрии. Вращения (поворотная). Греческое слово симметрия означает «пропорциональность», «гармония». Два вида симметрии. Горизонтальная.

«Симметрия в искусстве» — Iii.2. Периодичность в живописи. Элемент повторяемости, сходства облегчает восприятие правильной формы. Суриков «Утро стрелецкой казни». Живописцы эпохи Возрождения часто строили свои композиции по законам симметрии. Заключение. Ф.Бэкон. Симметричными были многие древние мозаики. Москва. Гой «Расстрел повстанцев «.

«О симметрии» — Рвал Эол алоэ, лавр. Палиндром — это абсолютное проявление симметрии в литературе. Симметрия – вокруг нас Геометрия. Орнамент. Палиндром В.Набокова: Я ел мясо лося, млея. Задачи. Симметрия в быту. Знакомство учащихся с симметрией в литературе, в архитектуре, природе, технике, быту…. Симметрия в технике.

«Задания на симметрию» — Икосаэдр. Центр симметрии. Пятиугольная призма. Грани. Ромбокубооктаэдр. Курносый куб. Додекаэдр. Сколько осей симметрии имеет шар. Фигура. Центральная симметрия. Кубооктаэдр. Икосододекаэдр. Приведите примеры пространственных фигур. Куб. Какие оси симметрии имеет кубооктаэдр. Плоскости симметрии. Правильная четырехугольная пирамида.

«Задачи по осевой симметрии» — Какая фигура называется симметричной. Две фигуры F и F’ называются симметричными. Сколько осей симметрии имеет восьмиугольник. Треугольник A’B’C’ симметричен треугольнику ABC. Какие точки называются симметричными. Осевая симметрия переводит точку А в точку А’. Какие две фигуры называются симметричными.

Курносый куб

Курносый куб
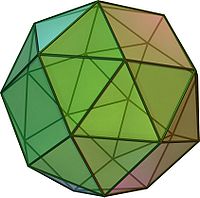На иллюстрации показан «левый» вариант (здесь можно посмотреть вращающуюся модель)
Тип	Полуправильный многогранник (архимедово тело)
Грани	треугольники (32), квадраты (6)
Граней	38
Рёбер	60
Вершин	24
Граней при вершине	5
Группа симметрии	Октаэдрическая (O)
Двойственный многогранник	Пентагональный икоситетраэдр

Курносый куб — полуправильный многогранник (архимедово тело) с 38 гранями, составленный из 6 квадратов и 32 правильных треугольников. В каждой из его 24 одинаковых вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными.

Имеет 60 рёбер равной длины.

Название «курносый куб» (лат. cubus simus ) дал этому многограннику Иоганн Кеплер в трактате 1619 года «Гармония мира». Гарольд Коксетер, отметив, что многогранник родственен октаэдру в той же мере, что и кубу, предлагал называть его «курносым кубооктаэдром».

В отличие от большинства других архимедовых тел, курносый куб (наряду с курносым додекаэдром) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».

При определении метрических свойств курносого куба приходится решать кубические уравнения и пользоваться кубическими корнями — тогда как для зеркально-симметричных архимедовых тел и для платоновых тел не требуется ничего сложнее квадратных уравнений и квадратных корней. Поэтому курносый куб, в отличие от платоновых и большинства архимедовых тел, не допускает евклидова построения [1] . То же верно и для курносого додекаэдра.

Важную роль при описании метрических свойств курносого куба играет константа трибоначчи:

t = 1 3 ( 1 + 19 − 3 33 3 + 19 + 3 33 3 ) ≈ 1 , 8392868. >left(1+ ] >>>+ ] >>>right)approx 1,8392868.> .

Если усечённый куб имеет ребро длины a , его площадь поверхности и объём выражаются как

S = ( 6 + 8 3 ) a 2 ≈ 19 , 8564065 a 2 , >right)a^ approx 19,8564065a^ ,> V = 613 t + 203 9 ( 35 t − 62 ) a 3 ≈ 7 , 8894774 a 3 . >>;a^ approx 7,8894774a^ .>

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

R = 3 − t 4 ( 2 − t ) a ≈ 1 , 3437134 a ; >>;aapprox 1,3437134a;>

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

ρ = R 2 − a 2 4 = 1 4 ( 2 − t ) a ≈ 1 , 2472232 a . — >>>= >>;aapprox 1,2472232a.>

Вписать в курносый куб сферу — так, чтобы она касалась всех граней, — невозможно. Радиус наибольшей сферы, которую можно поместить внутри курносого куба с ребром a (она будет касаться только всех квадратных граней в их центрах), равен

r 4 = R 2 − a 2 2 = t − 1 4 ( 2 − t ) a ≈ 1 , 1426135 a . = — >>>= >>;aapprox 1,1426135a.>

Расстояние от центра многогранника до центра любой треугольной грани превосходит r 4 > и равно

r 3 = R 2 − a 2 3 = t + 1 12 ( 2 − t ) a ≈ 1 , 2133558 a . = — >>>= >>;aapprox 1,2133558a.>

Двугранные углы между двумя треугольными гранями курносого куба равны arccos ⁡ 1 − 2 t 3 ≈ 153 , 23 ∘ , >approx 153,23^ ,> между квадратной и треугольной гранями arccos ⁡ ( − 1 − 2 3 t ) ≈ 142 , 98 ∘ . >>>right)approx 142,98^ .>

Куб (геометрия)

Куб
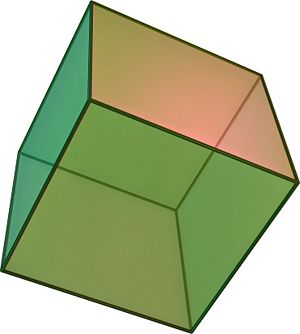Тип	Правильный многогранник
Грань	квадрат
Вершин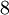
Рёбер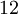
Граней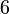
Граней при вершине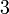
Длина ребра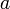
Площадь поверхности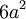
Объём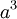
Радиус вписаной сферы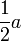
Радиус описаной сферы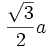
Угол наклона грани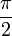
Угол наклона ребра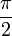
Точечная группа симметрии	Октаэдрическая (Oh)
Двойственный многогранник	Октаэдр

Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

В различных дисциплинах используются значения термина, имеющие отношения к тем или иным свойствам геометрического прототипа. В частности, в аналитике (

Содержание

Свойства куба

• В куб можно вписать тетраэдр двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба. Все шесть рёбер тетраэдра будут лежать на всех шести гранях куба и равны диагонали грани-квадрата.
• Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям.
• В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.
• Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.
• В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Тела кубической формы

В микромире

Примечания

См. также

Ссылки

Трёхмерные (Тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр)
Четырёхмерные (6 правильных многогранников)
Большей размерности
(только 3 типа правильных многогранников: n-мерный симплекс, n-мерный октаэдр, n-мерный куб)

Звёздчатый многогранник
(Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр)

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Куб (геометрия)» в других словарях:

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия пространств размерности, большей трех; термин применяется к тем пространствам, геометрия к рых была первоначально развита для случая трех измерений и только потом обобщена на число измерений n>3, прежде всего евклидово пространство,… … Математическая энциклопедия

N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным[1], и человеческие органы чувств рассчитаны на восприятие трёх измерений[2], N мерная… … Википедия

Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия

Конструктивная блочная геометрия — (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она позволяет создать сложную сцену или … Википедия

Координационная геометрия — Содержание 1 Молекулы 2 Координационные комплексы неорганических соединений … Википедия

Конструктивная сплошная геометрия — Конструктивная блочная геометрия (Constructive Solid Geometry, CSG) технология, используемая в моделировании твёрдых тел. Конструктивная блочная геометрия зачастую, но не всегда, является способом моделирования в трёхмерной графике и САПР. Она… … Википедия

Призма (геометрия) — У этого термина существуют и другие значения, см. Призма … Википедия

Объём (геометрия) — У этого термина существуют и другие значения, см. Объём (значения). Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого… … Википедия

Объем (геометрия) — Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении трёхмерных тел трёхмерного евклидова пространства.… … Википедия

24 грани из треугольников

Главная
• Список секций
• Математика
• УДИВИТЕЛЬНЫЙ МИР МНОГОГРАННИКОВ

УДИВИТЕЛЬНЫЙ МИР МНОГОГРАННИКОВ

Автор работы награжден дипломом победителя II степени

В раннем детстве все мы играли кубиками, пирамидками, с интересом разглядывали мамины и бабушкины серьги и кольца с камушками. Придя в школу, с удивлением узнали, что держали в руках правильные многогранники, а камушки не что иное, как октаэдры. На внеурочных занятиях по математике мы научились моделировать многогранники из бумаги и трубогранники из трубочек. Проблема при моделировании многогранников у нас возникла тогда, когда мы начали моделировать многогранник с шестигранными углами при вершине. У нас ничего не получилось! Пробовали мы сконструировать такой же трубогранник из трубочек и опять потерпели поражение. Поэтому нам захотелось больше узнать о многогранниках и выбрать тему работы: «Удивительный мир многогранников».

В своей научно-исследовательской работе мы решили изучить виды и свойства многогранников, а также показать способы моделирования многогранников и трубогранников. Актуальность. Выбранная нами тема исследования имеет широкое применение в различных сферах. Многогранники интересны и сами по себе. Они имеют красивые формы. Формы многогранников находят широкое применение в конструировании сложных и красивых многогранных поверхностей, которые используются в реальных архитектурных проектах. Идёт это с глубокой древности. Пирамида – это норма тектоники – внутреннего устройства каменных зданий прошлого. «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии, а греческая архитектура – внешнее выражение геометрии Евклида. Прошли века, но роль геометрии не изменилась. Она по-прежнему остаётся грамматикой архитектора» — это высказывание принадлежит великому французскому архитектору Ле Корбюзье.

В своей работе мы выдвинули следующее предположение: можно ли моделировать звездчатый многогранник с шестигранными углами при всех вершинах. На основании вышесказанного мы ставим перед собой следующую цель: изучить виды многогранников и раскрыть тайны моделирования многогранников.

Для реализации поставленной цели нами были выдвинуты задачи:

1)Изучить соответствующую историческую и математическую литературу.

2) Расширить знания о многогранниках, изучить их свойства.

3) Раскрыть тайны моделирования многогранников.

4) Исследовать способы создания различных моделей многогранников и трубогранников.

5) Показать практическое применение данной темы.

6) Разработать мастер классы и пособие по моделированию многогранников и трубогранников.

Для решения задач мы применили следующие методы исследования: аналитические методы, практическое моделирование, анализ, фотофиксация. Объект исследования: модели различных многогранников. Данная исследовательская работа реализуется в предметных рамках математики и геометрии, также можно использовать на уроках черчения, химии и биологии. Пособие по моделированию многогранников может быть использовано для внеурочной деятельности.

Правильные многогранники

Немного о многогранниках

Многогранником называется фигура, поверхность которого состоит из конечного числа плоских многоугольников, которые называют гранями. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника. Ни одни геометрические тела не обладают таким совершенством и красотой, как многогранники.

Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости каждой его грани.

Правильным называют выпуклый многогранник, у которого все элементы одного и того же вида равны, т. е. все ребра равны, все углы на гранях равны и все двугранные углы равны.

Существует только 5 правильных многогранников (тел Платона), 13 полуправильных многогранников, открытых Архимедом, бесконечные серии полуправильных многогранников, 4 типа правильных звёздчатых многогранников. (ПРИЛОЖЕНИЕ ).

Правильный тетраэдр составлен из 4-х равносторонних треугольников. Каждая его вершина является вершиной 3-х треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180 0 .

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной 4-х треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 0 .

Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 0 .

Гексаэдр (куб) составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 0 .

Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 0 .

Эти многогранники носят название правильные Платоновы тела – по имени древнегреческого философа Платона (ок. 428 – ок. 348 до н.э.).

Совершенство форм, красивые математические закономерности, присущие правильным многогранникам, явились причиной того, что им приписывались различные магические свойства. Это связано с числом их граней. В переводе с греческого языка:

«эдрон» – грань, «тетра» – четыре; «гекса» – шесть; «окто» – восемь; «додека» – двенадцать; «икоси» – двадцать.

В древности они олицетворяли: землю, воздух, воду, солнце, космос.

Тетраэдр – четырёхгранник — символизировал огонь, т.к. его вершина устремлена вверх.

Гексаэдр (куб) – шестигранник — землю, как самый устойчивый.

Октаэдр – восьмигранник — воздух, как самый воздушный.

Додекаэдр – двенадцатигранник — воплощал в себе все сущее, символизировал все мироздание, считался главным.

Икосаэдр — двадцатигранник — воду, т.к. он самый обтекаемый.

Полуправильные многогранники

У правильных многогранников все грани – правильные равные одноименные многоугольники и все многогранные углы равны. Но есть и такие многогранники, у которых все многогранные углы равны, а грани – правильные, но разноименные многоугольники. Многогранники такого типа называются равноугольно полуправильными многогранниками. Впервые многогранники такого типа открыл Архимед (287 – 212 гг. до н.э). Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда (ПРИЛОЖЕНИЕ)

Перечислим их: первые пять многогранников очень просто получить из пяти правильных многогранников операцией «усечения», которая состоит в отсечении плоскостями углов многогранника.

1.Усеченный тетраэдр – многогранник, который получается при последовательном срезании каждой из вершин тетраэдра. Многогранник имеет 12 вершин, 18 ребер, 8 граней. Гранями являются 4 правильных шестиугольника и 4 правильных треугольника. В каждой из вершин сходятся по 2 шестиугольника и треугольник.

2.Усечённый октаэдр – многогранник, который получается при последовательном срезании каждой из вершин октаэдра. Многогранник имеет 24 вершины, 36 ребер, 14 граней. Гранями являются 8 правильных шестиугольников и 6 правильных треугольника. В каждой из вершин сходятся по 2 шестиугольника и квадрат.

3.Усечённый икосаэдр – многогранник, который получается при последовательном срезании каждой из вершин икосаэдра. Многогранник имеет 60 вершины, 90 ребер, 32 граней. Гранями являются 12 правильных пятиугольников и 12 правильных шестиугольника. В каждой из вершин сходятся по 2 шестиугольника и пятиугольник. Каждый из пятиугольников со всех сторон окружён шестиугольниками. Усеченный икосаэдр очень напоминает изображение футбольного мяча.

4.Усечённый гексаэдр (усечённый куб) – многогранник, который получается при последовательном срезании каждой из вершин гексаэдра. Многогранник имеет 24 вершины, 36 ребер, 14 граней. Гранями являются 6 правильных восьмиугольника и 8 правильных треугольника. В каждой из вершин сходятся по 2 восьмиугольника и треугольник.

5.Усечённый додекаэдр — многогранник, который получается при последовательном срезании каждой из вершин додекаэдра. Многогранник имеет 60 вершины, 90 ребер, 32 граней. Гранями являются 12 правильных десятиугольников и 20 правильных треугольника. В каждой из вершин сходятся по 2 десятиугольника и треугольник

6.Кубооктаэдр. Если теперь в кубе провести плоскости через середины ребер, выходящих из одной вершины, получим еще один шестой равноугольно полуправильный многогранник – кубооктаэдр. Многогранник имеет 12 вершины, 24 ребер, 14 граней. Гранями являются 6 квадратов и 8 правильных треугольников. В каждой из вершин сходятся по 2 квадрата и по 2 треугольника.

7.Икосадодекаэдр. Если в додекаэдре провести плоскости через середины его ребер, выходящих из одной вершины, получим многогранник, который называется икосадодекаэдром. Многогранник имеет 30 вершин, 60 ребер, 32 граней. Гранями являются 12 правильных пятиугольников и 20 правильных треугольников. В каждой из вершин сходятся по 2 правильных пятиугольника и по 2 правильных треугольника.

8.Усеченный кубооктаэдр — многогранник, который получается при последовательном срезании каждой из вершин кубооктаэдра. Многогранник имеет 48 вершин, 72 ребра, 26 граней. Гранями являются 8 правильных шестиугольника, 6 правильных восьмиугольника и 12 квадрата. В каждой из вершин сходятся 1 шестиугольника, 1 восьмиугольник и квадрат.

9.Усеченный икосадодекаэдр — многогранник, который получается при последовательном срезании каждой из вершин икосадодекаэдра. Многогранник имеет 120 вершин, 180 ребра, 62 граней. Гранями являются 20 правильных шестиугольника, 12 правильных десятиугольника и 30 квадратов. В каждой из вершин сходятся 1 квадрат, 1 десятиугольник и 1 шестиугольник.

10.Ромбокубооктаэдр он состоит из граней куба и октаэдра, к которым добавлены еще 12 квадратов. Многогранник имеет 24 вершин, 28 ребра, 26 граней. Гранями являются 18 квадратов и 8 правильных треугольников. В каждой из вершин сходятся по 3 квадрата и 1 треугольник.

11.Ромбоикосододекаэдр состоит из граней икосаэдра, додекаэдра и еще 30 квадратов. Многогранник имеет 60 вершин, 120 ребер, 62 граней. Гранями являются 30 квадратов, 12 правильных пятиугольников и 20 правильных

треугольников. В каждой из вершин сходятся по 2 квадрата, 1 пятиугольник и 1 треугольник.

12.«Плосконосый» куб состоит из граней куба или додекаэдра, окруженных правильными треугольниками. Многогранник имеет 24 вершин, 60 ребер, 38 граней. Гранями являются 6 квадратов и 32 правильных треугольников. В каждой из вершин сходятся 1 квадрат и по 4 треугольника.

13.«Плосконосый» додекаэдр состоит из граней куба или додекаэдра, окруженных правильными треугольниками. Многогранник имеет 60 вершин, 150 ребер, 92 грани. Гранями являются 12 правильных пятиугольников, 80 правильных треугольников. В каждой из вершин сходятся 1 пятиугольник и по 4 треугольника.

1.3 Звездчатые многогранники

Кроме полуправильных многогранников, из правильных многогранников – Платоновых тел можно получить так называемые правильные звездчатые многогранники.

Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам. Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. В отличие от пяти классических правильных многогранников, данные многогранники не являются выпуклыми телами. Тетраэдр, куб, октаэдр не имеют звездчатых форм, додекаэдр имеет три, а икосаэдр – одну звездчатую форму.

В 1811 году Огюстен Лу Коши установил, что существуют всего 4 правильных звёздчатых тела (они называются телами Кеплера — Пуансо), которые не являются соединениями платоновых и звёздчатых тел.

К ним относятся открытые в 1619 году Иоганном Кеплером малый звёздчатый додекаэдр и большой звёздчатый додекаэдр, а также большой додекаэдр и большой икосаэдр, открытые в 1809 году Луи Пуансо. (ПРИЛОЖЕНИЕ). Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кеплера — Пуансо.

Полуправильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются правильные или звёздчатые многоугольники, но не обязательно одинаковые. При этом строение всех вершин должно быть одинаковым. Г. Коксетер, М. Лонге-Хиггинс и Дж. Миллер в 1954 году перечислили 53 таких тела и выдвинули гипотезу о полноте своего списка. Только значительно позже в 1969 году Сопову С. П. удалось доказать, что представленный ими список многогранников действительно полон. Со всеми этими видами звездчатых многогранников вы можете ознакомиться на сайте http://zvzd3d.ru/FromBumaga.html.

2.Свойства выпуклых многогранников

2.1 Сумма углов выпуклого многогранника

Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.

Исследуем, какие многогранники могут получиться, если в гранях правильные треугольники, четырёхугольники, пятиугольники, шестиугольники и т.д.

1.Пусть грани правильного многогранника – правильные треугольники. Каждый угол правильного треугольника по 60 о . Если при вершине многогранного угла n плоских углов, то

60n о . Если при вершине многогранного угла n плоских углов, то

90n о . Если при вершине многогранного угла n плоских углов, то

108 n о . Если при вершине многогранного угла n плоских углов, то

📽️ Видео